Лекция 6 Матрицы
|
Определение и некоторые свойства определителей порядка n. Сложение матриц, умножение матрицы на число, умножение матриц. Свойства этих операций |
6.1. Основные понятия
Определение 1. Матрицей называется прямоугольная таблица чисел.
Для обозначения матрицы используются круглые скобки или сдвоенные вертикальные линии:
.
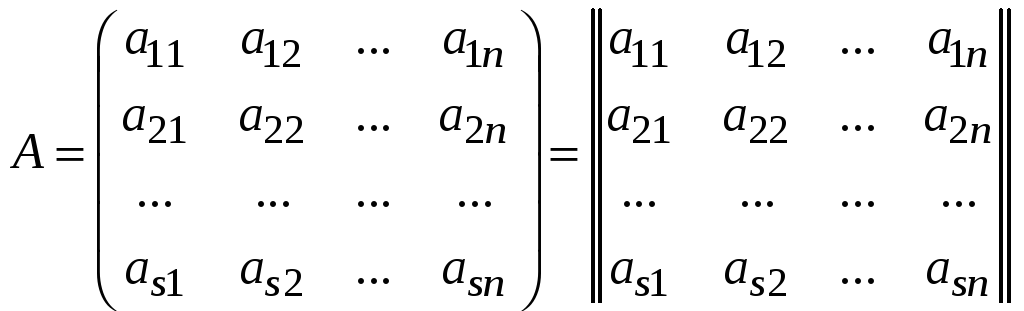Числа, составляющие матрицу, называются
ее элементами, элемент
матрицы
расположен в ее
-й
строке и
-м
столбце.
Числа
и
(число строк и столбцов матрицы) называются
ее порядками.
Говорят также, что
- матрица размером
.
Если
,
матрица
называется квадратной.
Для краткой записи используется также
обозначение
(или
)
и далее указывается, в каких пределах
изменяются
и
,
например,
,
,
.
(Запись читается так: матрица
с элементами
,
изменяется от
до
,
- от
до
.)
Среди квадратных матриц отметим
диагональные матрицы, у которых все
элементы с неравными индексами (
)
равны нулю:
.
Будем говорить, что элементы
расположены на главной диагонали.
Диагональная матрица вида
называется единичной матрицей.
В дальнейшем будут встречаться матрицы вида
и
,
которые называются треугольными матрицами, а также матрицы, состоящие из одного столбца:
и одной строки:
(матрица-столбец и матрица-строка).
Матрица, все элементы которой равны нулю, называется нулевой.
6.2. Определители порядка n
Пусть дана квадратная матрица порядка
:
.
(6.1)
Составим всевозможные произведения
элементов матрицы, расположенных в
разных строках и разных столбцах, т.е.
произведения вида
.
(6.2)
Число произведений вида (6.2) равно
(примем этот факт без доказательства).
Будем считать все эти произведения
членами определителя порядка
,
соответствующего матрице (6.1).
Вторые индексы множителей в (6.2) составляют
перестановку первых
натуральных чисел
.
Говорят, что числа
и
в перестановке составляют инверсию,
если
,
а в перестановке
расположено раньше
.
Пример 1. В
перестановке шести чисел,
,
числа
и
,
и
,
и
,
и
,
и
составляют инверсии.
Перестановка называется четной, если число инверсий в ней четно, и нечетной, если число инверсий в ней нечетно.
Пример 2.
Перестановка
- нечетная, а перестановка
- четная (
инверсий).
Определение 2. Определителем
порядка
,
соответствующим матрице (6.1),
называется алгебраическая сумма
членов, составленная следующим
образом: членами определителя служат
всевозможные произведения
элементов матрицы, взятых по одному
из каждой строки и каждого столбца,
причем слагаемое берется со знаком "+",
если множество вторых индексов является
четной перестановкой чисел
,
и со знаком "–", если нечетной.
Обозначать определитель матрицы (6.1) принято так:
.
Замечание.
Определение 2 для
и
приводит к уже знакомым нам определителям
2-го и 3-го порядка:
,
.
Транспонированием вокруг главной
диагонали матрицы
называется переход к матрице
,
для которой строки матрицы
являются столбцами, а столбцы - строками:
.
Будем говорить, что определитель
получен транспонированием определителя
.