
13.2. Ортогональные и ортонормированные базисы в
Определение
3.
Пусть
![]() - евклидово пространство,
- евклидово пространство,
![]() ,
,
![]() .
Векторы
.
Векторы
![]() и
и
![]() называются ортогональными,
если
называются ортогональными,
если
![]() .
.
Определение
4.
Система
векторов
![]() называется ортогональной системой
векторов в евклидовом пространстве
называется ортогональной системой
векторов в евклидовом пространстве
![]() ,
если
,
если
![]() при
при
![]() .
.
Справедливо следующее утверждение.
Теорема
2.
В
евклидовом пространстве
![]() всякая система ненулевых ортогональных
векторов линейно независима.
всякая система ненулевых ортогональных
векторов линейно независима.
Доказательство.
Пусть
![]() - произвольная ортогональная система
векторов в
- произвольная ортогональная система
векторов в
![]() ;
;
![]()
![]() .
.
Пусть
![]() .
(13.5)
.
(13.5)
Умножим
обе части (13.5) скалярно на
![]() :
:
![]() .
(13.6)
.
(13.6)
Поскольку
система векторов
![]() ортогональна, то верны равенства
ортогональна, то верны равенства
![]() ,…,
,…,
![]() ;
следствие а) из аксиом дает
;
следствие а) из аксиом дает
![]() ;
согласно аксиоме 4
;
согласно аксиоме 4
![]() .
Тогда из равенства (13.6) получим
.
Тогда из равенства (13.6) получим
![]() .
.
Аналогично,
скалярно умножая (13.5) последовательно
на
![]() ,
получим
,
получим
![]() ,
следовательно, система
,
следовательно, система
![]() линейно независима.
линейно независима.
Теорема доказана.
Опишем
процесс
построения ортогонального базиса
в линейной оболочке любых
![]() линейно независимых векторов.
линейно независимых векторов.
Пусть
![]() линейно независимы.
линейно независимы.
Шаг
1.
Примем
![]() .
.
Шаг
2.
Примем
![]() .
Отметим, что
.
Отметим, что
![]() ,
так как
,
так как
![]() является линейной комбинацией
является линейной комбинацией
![]() и
и
![]() ,
причем
,
причем
![]() и
и
![]() линейно независимы (линейная комбинация
векторов
линейно независимы (линейная комбинация
векторов
![]() и
и
![]() с коэффициентами, один из которых, а
именно коэффициент при
с коэффициентами, один из которых, а
именно коэффициент при
![]() ,
заведомо отличен от нуля, не может
равняться
,
заведомо отличен от нуля, не может
равняться
![]() ).
).
Подберем
![]() так, чтобы
так, чтобы
![]() :
:
![]() и
и
 .
.
Шаг
3.
Примем
![]() .
Отметим, что
.
Отметим, что
![]() ,
так как
,
так как
![]() является линейной комбинацией
является линейной комбинацией
![]() ,
,
![]() и
и
![]() ,
а эти векторы линейно независимы.
Подберем
,
а эти векторы линейно независимы.
Подберем
![]() и
и
![]() так, чтобы
так, чтобы
![]() и
и
![]() .
.

Отсюда
![]() ,
,
![]() .
.
Шаг
4.
Пусть уже построена ортогональная
система ненулевых векторов
![]() ,
причем
,
причем
![]() ,
,
![]() является линейной комбинацией векторов
является линейной комбинацией векторов
![]() .
Положим
.
Положим
![]() .
.
Вектор
![]() ,
так как является линейной комбинацией
линейно независимых векторов
,
так как является линейной комбинацией
линейно независимых векторов
![]() с коэффициентами, один из которых, а
именно коэффициент при
с коэффициентами, один из которых, а
именно коэффициент при
![]() ,
заведомо отличен от нуля (поскольку
,
заведомо отличен от нуля (поскольку
![]() не входит в
не входит в
![]() ).
).
Коэффициенты
![]() подберем так, чтобы
подберем так, чтобы
![]() был ортогонален векторам
был ортогонален векторам
![]() :
:
![]() .
.
Отсюда
![]()
![]()
и
![]() ,
,
![]() .
.
Продолжая
процесс, построим ортогональную систему
векторов
![]() ,
причем
,
причем
![]() ,
,
![]() ,
откуда в силу теоремы 2 следует, что
,
откуда в силу теоремы 2 следует, что
![]() линейно независимы. Линейная оболочка
линейно независимы. Линейная оболочка
![]() векторов
векторов
![]() является подпространством размерности
является подпространством размерности
![]() (
(![]() ),
а это означает, что
),
а это означает, что
![]() - базис в
- базис в
![]() (по построению - ортогональный).
(по построению - ортогональный).
Описанный выше процесс носит название процесса ортогонализации Шмидта.
Пример
3.
![]() - евклидово пространство геометрических
векторов. Применяя процесс ортогонализации
Шмидта, построить ортогональный базис
в подпространстве, натянутом на векторы
- евклидово пространство геометрических
векторов. Применяя процесс ортогонализации
Шмидта, построить ортогональный базис
в подпространстве, натянутом на векторы
![]() и
и
![]() .
.
Полагаем
![]() ,
,
![]() .
.
Подбираем
![]() :
:
![]()
![]() ,
,
о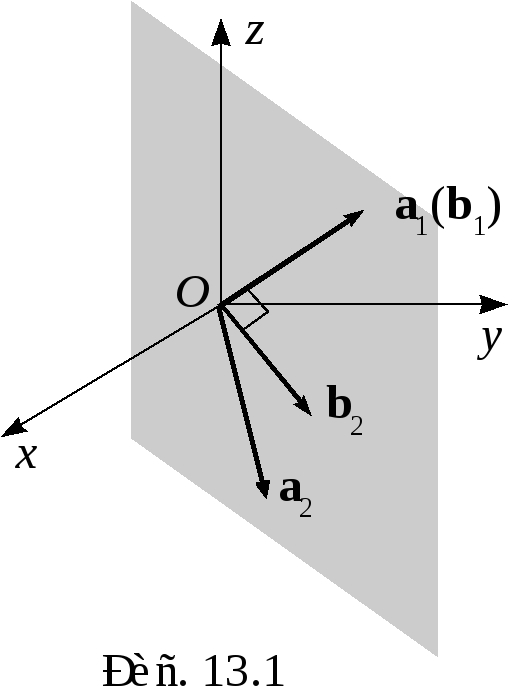 ткуда
ткуда
![]() .
.
Итак,
![]() ,
и базис в линейной оболочке
,
и базис в линейной оболочке
![]() составляют векторы
составляют векторы
![]() ,
,
![]() .
.
Геометрический
смысл процедуры иллюстрирует рис. 13.1.
Подпространство
![]() ,
натянутое на векторы
,
натянутое на векторы
![]() ,
- плоскость, проходящая через
,
- плоскость, проходящая через
![]() и векторы
и векторы
![]() и
и
![]() ,
приведенные к точке
,
приведенные к точке
![]() .
В этой плоскости построен базис
.
В этой плоскости построен базис
![]() ,
,
![]() такой, что
такой, что
![]() .
.
Упражнения.
1.
Проверить ортогональность системы
векторов
![]() и
и
![]() в евклидовом пространстве
в евклидовом пространстве
![]() и дополнить ее до ортогонального базиса.
и дополнить ее до ортогонального базиса.
2.
Применяя процесс ортогонализации
Шмидта, построить ортогональный базис
в линейной оболочке системы векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Замечание.
Всякое евклидово пространство
![]() обладает ортогональными базисами.
обладает ортогональными базисами.
Действительно,
пусть
![]() - евклидово пространство,
- евклидово пространство,
![]() ,
,
![]() - базис в
- базис в
![]() .
Применим к базису
.
Применим к базису
![]() процесс ортогонализации Шмидта, получим
некоторый ортогональный базис в
процесс ортогонализации Шмидта, получим
некоторый ортогональный базис в
![]() .
.
Определение
5.
Вектор
![]() называется нормированным,
если
называется нормированным,
если
![]() .
.
Если
![]() ,
то нормированием
называется переход к вектору
,
то нормированием
называется переход к вектору
![]() (
(![]() является нормированным, так как
является нормированным, так как
![]()
![]() и, следовательно,
и, следовательно,
![]() ).
).
Определение
6.
Система
векторов
![]() в евклидовом пространстве
в евклидовом пространстве
![]() называется ортонормированной системой,
если
называется ортонормированной системой,
если
![]()
Всякое евклидово пространство обладает ортонормированными базисами.
В
самом деле, ранее было показано, что
всякое евклидово пространство обладает
ортогональными базисами. Возьмем в
![]() произвольный ортогональный базис
произвольный ортогональный базис
![]() и нормируем все его векторы, т.е. перейдем
к системе векторов
и нормируем все его векторы, т.е. перейдем
к системе векторов
![]() .
(13.7)
.
(13.7)
Система
(13.7) - ортонормированный базис в
![]() .
.
Пример
4.
![]() - евклидово пространство геометрических
векторов. Указать какой-нибудь
ортонормированный базис в линейной
оболочке векторов
- евклидово пространство геометрических
векторов. Указать какой-нибудь
ортонормированный базис в линейной
оболочке векторов
![]() и
и
![]() .
.
В
примере 3 был построен ортогональный
базис
![]() ,
,
![]() в
в
![]() .
.
Имеем
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Векторы
![]() -
ортонормированный базис в
-
ортонормированный базис в
![]() .
.
Упражнения.
1.
Указать какой-нибудь ортонормированный
базис в линейной оболочке векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2.
![]() - евклидово пространство геометрических
векторов. Построить какой-нибудь
ортонормированный базис в линейной
оболочке векторов
- евклидово пространство геометрических
векторов. Построить какой-нибудь
ортонормированный базис в линейной
оболочке векторов
![]() ,
,
![]() и
и
![]() .
.
Теорема
3.
Пусть
![]() - евклидово пространство,
- евклидово пространство,
![]() (I)
– базис в
(I)
– базис в
![]() .
Базис
.
Базис
![]() является ортонормированным тогда и
только тогда, когда для любых векторов
является ортонормированным тогда и
только тогда, когда для любых векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() скалярное произведение выражается
равенством
скалярное произведение выражается
равенством
![]() .
.
Доказательство.
Необходимость. Пусть
базис (I)
– ортонормированный, т.е.
![]()
Тогда
 .
.
Но
во внутренней сумме всего одно слагаемое
отлично от нуля при
![]() (
(![]() ).
Таким образом,
).
Таким образом,
![]() .
.
Достаточность.
Пусть
базис (I)
таков, что
![]() ,
,
![]()
![]() .
Для векторов базиса справедливы
разложения
.
Для векторов базиса справедливы
разложения
![]() ,
,
![]() .
.
В
силу этих разложений получим
![]() ,
,
![]() ,
– и базис (I)
– ортонормированный.
,
– и базис (I)
– ортонормированный.
