5.5. Классификация поверхностей 2-го порядка по их каноническим уравнениям
Пусть
- декартова система координат.
Алгебраической поверхностью 2-го порядка
называется поверхность, уравнение
которой относительно
имеет вид
,
(5.29)
не
равны одновременно нулю.
Уравнение
(5.29) может определять относительно
так называемую вырожденную поверхность
(пару плоскостей, точку, пустое множество
и т.д.).
Если (5.29) – невырожденная поверхность, то некоторым преобразованием декартовых координат ее уравнение может быть приведено к каноническому виду (примем этот факт без доказательства).
П
о
каноническому виду определяется тип
поверхности:
1) эллипсоид трехосный (рис.5.17):
;
2) гиперболоид:
а) однополостный (рис.5.18):
;
б) двуполостный (рис.5.19):
;
3
)
конус 2-го порядка (рис. 5.20):
4) параболоид:
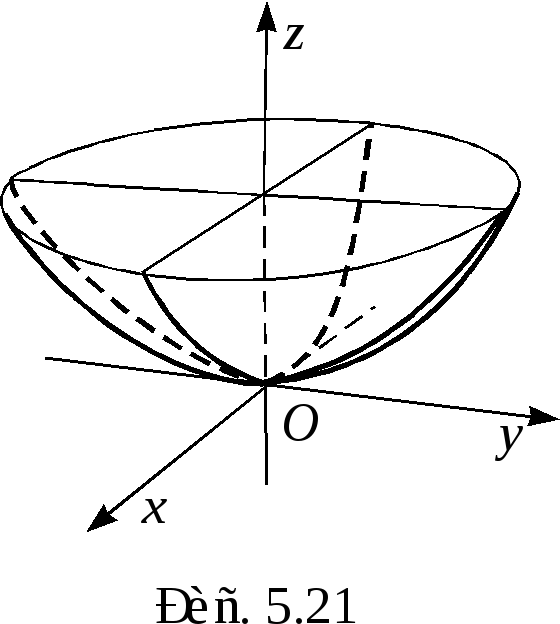
а) эллиптический (рис. 5.21):
;
б) гиперболический (рис. 5.22);
;
5
)
цилиндр 2-го порядка (рис. 5.23):
а) эллиптический:
;
б) гиперболический (рис. 5.24):
;
в) параболический (5.25):
.
Основным методом исследования формы поверхности по ее уравнению является метод сечений.
Метод
сечений заключается в том, что в уравнении
поверхности последовательно полагают
,
,
(т.е. «пересекают» поверхность плоскостями,
параллельными координатным) и в
зависимости от вида кривой, получающейся
в сечении, делают заключение о типе
поверхности и ее расположении.
Пример 4. Методом сечений исследовать форму и построить поверхность
.
(5.30)
Положим
,
или
.
Отметим,
что при
точек пересечения нет (следовательно,
в области
точек поверхности нет); при
уравнение (5.30) определяет эллипс с
полуосями
и
;
при
точка
(поверхность проходит через начало
координат).
Пусть
,
тогда
,
или
,
или
– парабола с
,
смещенная по оси
вверх на
.
Пусть
,
тогда
,
или
,
или
– парабола с
,
смещенная по оси
вверх на
.
Н
а
рис.5.26 изображен эллипс, получающийся
в сечении плоскостью
(полуоси
).
Представив общий характер кривых, получающихся в сечении, уже нетрудно выбрать из девяти поверхностей соответствующую уравнению (5.30).
Итак, поверхность – эллиптический параболоид (см. рис. 5.26.).