
- •Глава 8. Квадратичные формы
- •§ 1. Линейные и билинейные формы
- •§ 2. Квадратичные формы
- •§ 3. Изменение матрицы квадратичной формы при изменении базиса
- •§ 4. Положительно определённые квадратичные формы
- •§ 5. Приведение квадратичной формы к каноническому виду ортогональным преобразованием
- •§ 6. Применение теории квадратичных форм к кривым и поверхностям второго порядка
§ 5. Приведение квадратичной формы к каноническому виду ортогональным преобразованием
Будем
называть линейное преобразование
переменных
![]() ортогональным,
если матрица
ортогональным,
если матрица
![]() ортогональная,
т.е.
ортогональная,
т.е.
![]() Ортогональное преобразование можно
интерпретировать как преобразование
координат, осуществляющееся при переходе
от одного ортонормированного базиса
линейного пространства к другому его
ортонормированному базису. Геометрически
такое преобразование является движением
системы координат пространства
Ортогональное преобразование можно
интерпретировать как преобразование
координат, осуществляющееся при переходе
от одного ортонормированного базиса
линейного пространства к другому его
ортонормированному базису. Геометрически
такое преобразование является движением
системы координат пространства![]() при котором начало координат является
неподвижной точкой. На плоскости
при котором начало координат является
неподвижной точкой. На плоскости![]() это поворот системы координат вокруг
начала координат на какой-либо угол,
симметрия относительно прямой, проходящей
через начало координат, и комбинации
поворотов и симметрий: в пространстве
это поворот системы координат вокруг
начала координат на какой-либо угол,
симметрия относительно прямой, проходящей
через начало координат, и комбинации
поворотов и симметрий: в пространстве![]() повороты
вокруг прямых, симметрии относительно
плоскостей и их комбинации и т.д. Имеет
место
повороты
вокруг прямых, симметрии относительно
плоскостей и их комбинации и т.д. Имеет
место
Теорема
7. Всякую квадратичную
форму от
![]() переменных можно ортогональным
преобразованием координат
переменных можно ортогональным
преобразованием координат![]() привести к каноническому виду
привести к каноническому виду
![]() (10)
(10)
причём
если
![]() матрица
квадратичной формы
матрица
квадратичной формы![]() то
то![]() собственные
векторы матрицы
собственные
векторы матрицы![]() а связь старых и новых переменных
определяется формулами
а связь старых и новых переменных
определяется формулами![]()
![]() где
где![]() – матрица перехода от одного
ортонормированного базиса к другому.
– матрица перехода от одного
ортонормированного базиса к другому.
Для
того, чтобы привести данную квадратичную
форму к каноническому виду ортогональным
преобразованием, поступают следующим
образом. Матрица
![]() квадратичной формы (она обязательно
симметрическая) интерпретируется как
матрица симметрического линейного
оператора в ортонормированном базисе.
Его матрица будет иметь диагональный
вид (а значит, квадратичная форма
приведётся к каноническому виду) в
ортонормированном базисе из собственных
векторов этого оператора. Сформулируем
алгоритм приведения квадратичной формы.
квадратичной формы (она обязательно
симметрическая) интерпретируется как
матрица симметрического линейного
оператора в ортонормированном базисе.
Его матрица будет иметь диагональный
вид (а значит, квадратичная форма
приведётся к каноническому виду) в
ортонормированном базисе из собственных
векторов этого оператора. Сформулируем
алгоритм приведения квадратичной формы.
Находим собственные значения линейного оператора, решая характеристическое уравнение

Для каждого собственного значения находим собственные векторы, решая систему линейных уравнений
 (У этой системы мы должны найти
фундаментальную систему решений).
(У этой системы мы должны найти
фундаментальную систему решений).Если собственное значение
 имеет кратность, большую 1 (в
характеристическом уравнении), то
векторы из ф.с.р. могут оказаться не
ортогональными друг другу – в этом
случае к ним надо применить процесс
ортогонализации.
имеет кратность, большую 1 (в
характеристическом уравнении), то
векторы из ф.с.р. могут оказаться не
ортогональными друг другу – в этом
случае к ним надо применить процесс
ортогонализации.Нормируем найденные собственные векторы, т.е. каждый вектор делим на его длину.
Записываем канонический вид квадратичной формы и преобразование координат, приводящее её к этому виду.
Задача
8. Привести данную
квадратичную форму к каноническому
виду ортогональным преобразованием
координат:
![]()
Решение. Составим матрицу этой квадратичной формы:

Составим характеристическое уравнение:

Отсюда
получаем:
![]() Корни характеристического уравнения:
Корни характеристического уравнения:![]()
![]()
Для
![]() система уравнений, из которой находятся
собственные векторы, выглядит так:
система уравнений, из которой находятся
собственные векторы, выглядит так:

Её
фундаментальная система решений:
![]()
![]() Эти векторы не ортогональны друг другу,
поэтому применим к ним процесс
ортогонализации. Положим
Эти векторы не ортогональны друг другу,
поэтому применим к ним процесс
ортогонализации. Положим![]()
![]() и подберём
и подберём![]() так, чтобы было выполнено условие
так, чтобы было выполнено условие![]() Имеем:
Имеем:![]() т.е.
т.е.![]()
![]() Следовательно,
Следовательно,![]()
Запишем
теперь систему уравнений для
![]()
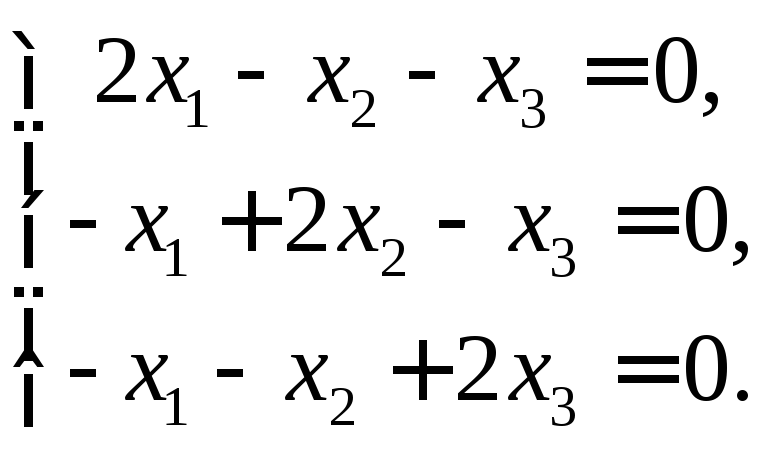
Её
ф.с.р. состоит из одного вектора:
![]() Этот
вектор ортогонален векторам
Этот
вектор ортогонален векторам![]() и
и![]()
Пронормируем
векторы
![]() разделив каждый вектор на его длину.
Получим ортонормированный базис из
собственных векторов:
разделив каждый вектор на его длину.
Получим ортонормированный базис из
собственных векторов:![]()
![]()
![]()
Матрица
перехода от исходного базиса
![]()
![]()
![]() к новому базису
к новому базису![]() равна:
равна:

По
формуле (10) в новых координатах квадратичная
форма будет иметь вид
![]() Старые координаты выражаются через
новые следующим образом:
Старые координаты выражаются через
новые следующим образом:

Обратные формулы:

т.е.

