Даны
точки
 и
и Составить уравнения прямых, проходящих
через концы отрезка
Составить уравнения прямых, проходящих
через концы отрезка перпендикулярно этому отрезку. Ответ:
перпендикулярно этому отрезку. Ответ:

При
каком
 прямые
прямые и
и перпендикулярны? Ответ:
перпендикулярны? Ответ:
Даны
точки
 и
и Найти точку пересечения прямой
Найти точку пересечения прямой с осью ординат. Ответ:
с осью ординат. Ответ: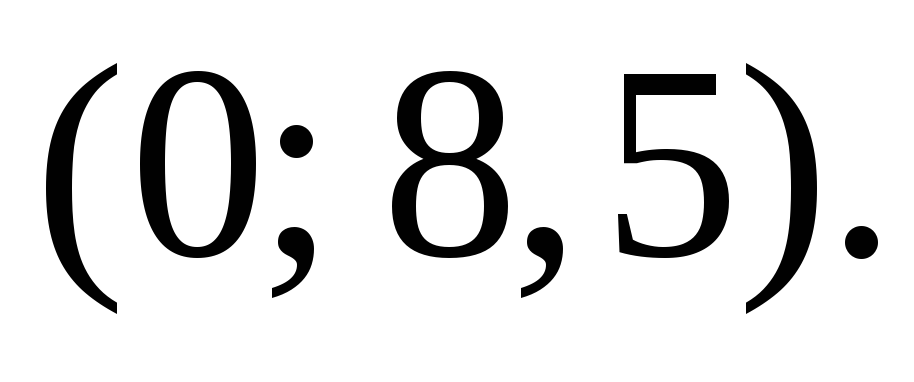
Составить
общее уравнение прямой, заданной
параметрическими уравнениями
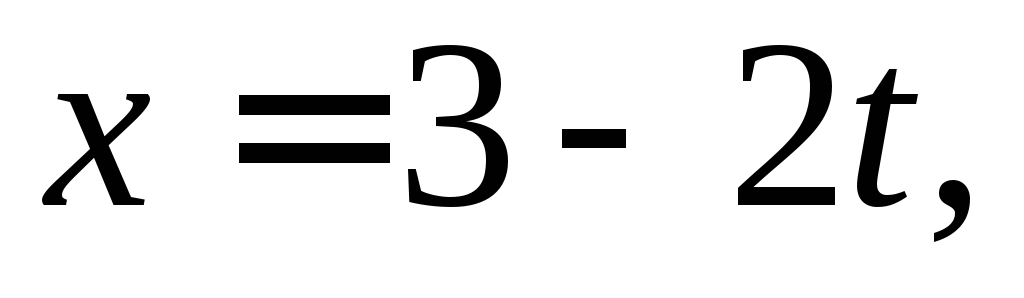
 Ответ:
Ответ:
Составить
уравнение средней линии
 треугольника
треугольника если
если

 Ответ:
Ответ:
Даны
точка
 и прямая
и прямая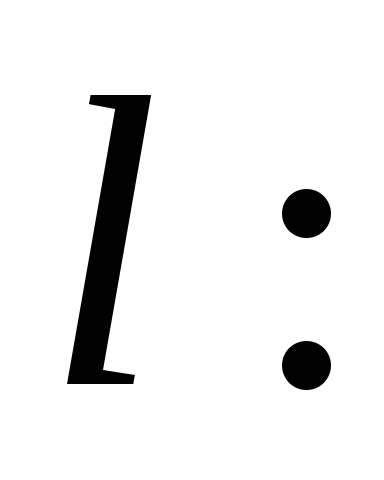
 Составить уравнение геометрического
места точек
Составить уравнение геометрического
места точек являющихся серединами отрезков
являющихся серединами отрезков где
где Ответ:
Ответ:
Составить
уравнение геометрического места точек,
равноудалённых от точек
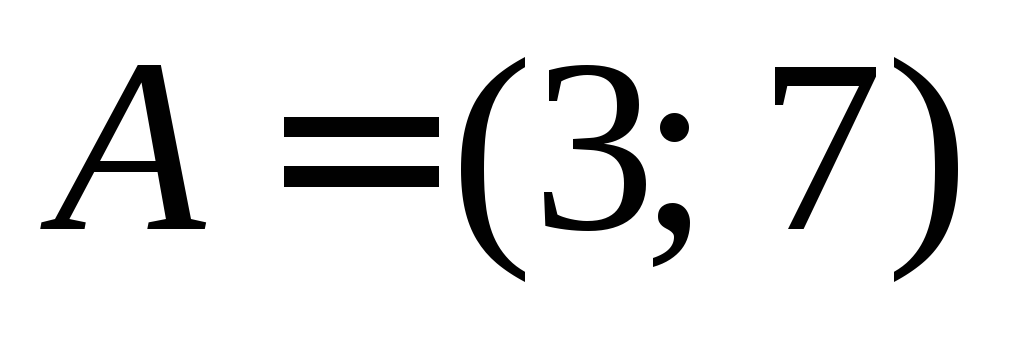 и
и Ответ:
Ответ:
Известно
уравнение стороны
 параллелограмма
параллелограмма
 его диагонали
его диагонали
 и вершина
и вершина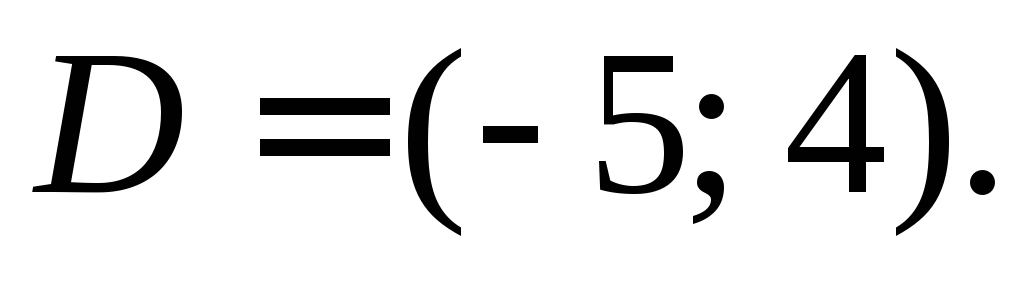 Найти координаты вершин
Найти координаты вершин
 и
и Ответ:
Ответ:


Найти
точку, симметричную точке
 относительно прямой
относительно прямой Ответ:
Ответ:
Через
точку
 провести прямую, отсекающую от осей
координат треугольник площадью 2. Ответ:
провести прямую, отсекающую от осей
координат треугольник площадью 2. Ответ:

Найти
расстояние между прямыми, заданными
параметрически:

 и
и
 Ответ:
Ответ:
На
прямой
 найти все точки, равноудалённые от
прямых
найти все точки, равноудалённые от
прямых и
и Ответ:
Ответ: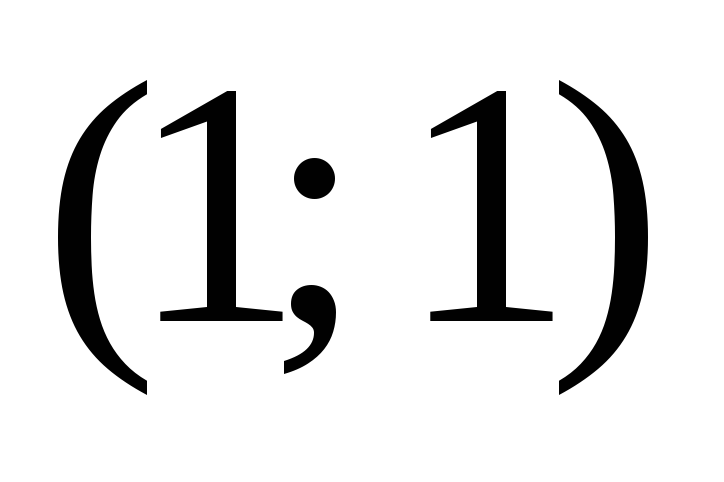 и
и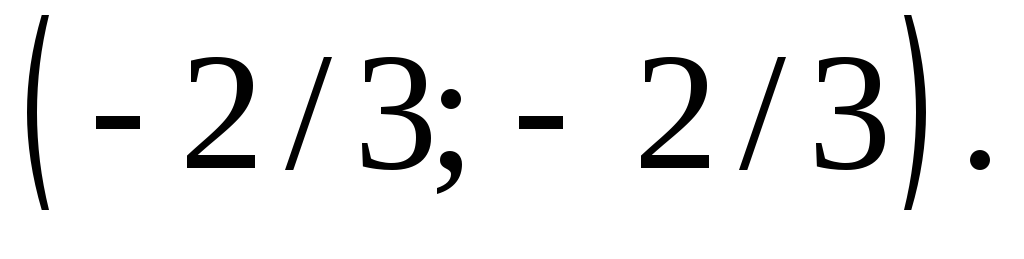
Написать
уравнение геометрического места точек,
для которых расстояние до прямой
 в 3 раза больше расстояния до прямой
в 3 раза больше расстояния до прямой Ответ: две прямые:
Ответ: две прямые: и
и по-другому:
по-другому:
Определить,
по одну или по разные стороны от прямой
 расположены точки
расположены точки и
и Ответ: по разные.
Ответ: по разные.
Определить,
лежит ли точка
 внутри угла
внутри угла если
если


 Ответ: лежит.
Ответ: лежит.
Определить,
точки
 и
и лежат в одном, в смежных или вертикальных
углах, образованных прямыми
лежат в одном, в смежных или вертикальных
углах, образованных прямыми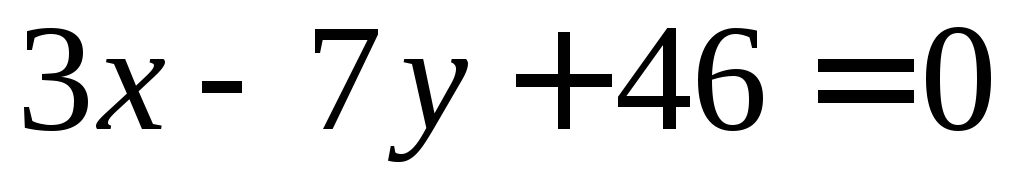 и
и Ответ: в вертикальных.
Ответ: в вертикальных.
Изобразить
на координатной плоскости множество
точек, удовлетворяющих системе неравенств

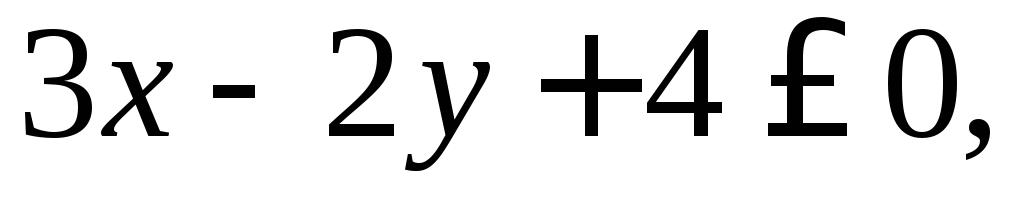

Поставить
вместо звёздочек знаки < или > так,
чтобы область плоскости, определяемая
неравенствами


 была ограниченной. Ответ: <, <, >.
была ограниченной. Ответ: <, <, >.

