
- •Глава 4. Плоскость и прямая в пространстве § 1. Векторное и смешанное произведение векторов
- •Выражение векторного произведения через координаты векторов
- •Геометрический смысл смешанного произведения
- •Выражение смешанного произведения через координаты векторов
- •Условия коллинеарности и компланарности векторов
- •Задачи для самостоятельного решения
- •§ 2. Уравнения прямых и плоскостей в пространстве
- •§ 3. Расстояние и отклонение точки от плоскости
- •§ 4. Расстояние от точки до прямой в пространстве. Расстояние между скрещивающимися прямыми
- •Задачи для самостоятельного решения
§ 3. Расстояние и отклонение точки от плоскости
Пусть
![]() – плоскость, заданная уравнением
– плоскость, заданная уравнением![]() и
и![]() – произвольная точка пространства.
Тогдарасстояние
– произвольная точка пространства.
Тогдарасстояние
![]() от точки
от точки![]() до плоскости
до плоскости
![]() выражается формулой
выражается формулой
![]() (10)
(10)
В
знаменателе этой дроби стоит длина
вектора
![]() – нормального вектора плоскости
– нормального вектора плоскости![]() Таким образом,чтобы
найти расстояние от точки до плоскости,
надо подставить координаты точки в
уравнение плоскости и разделить
полученное число на длину нормального
вектора; при
этом мы получим число, которое может
быть отрицательным – в этом случае
берём его по абсолютной величине.
Таким образом,чтобы
найти расстояние от точки до плоскости,
надо подставить координаты точки в
уравнение плоскости и разделить
полученное число на длину нормального
вектора; при
этом мы получим число, которое может
быть отрицательным – в этом случае
берём его по абсолютной величине.
Если в формуле (10) убрать знак модуля, то мы получим величину
![]() (11)
(11)
называемую
отклонением
точки
![]() от плоскости
от плоскости
![]()
Очевидно,
![]() и
и![]()
Замечание.
Определённое
по формуле
(11) отклонение
отличается от того отклонения, которое
принято в ряде учебников (а именно,
![]() если
если![]() и
и![]() если
если![]() ).
Мы будем пользоваться формулой (11).
).
Мы будем пользоваться формулой (11).
Геометрический
смысл отклонения
точки от плоскости точно такой же, как
у отклонения точки от прямой на плоскости
(см. раздел “Прямая на плоскости”). А
именно, отклонение
по абсолютной величине равно расстоянию,
причём
![]() если точка
если точка![]() находится от плоскости
находится от плоскости![]() по ту сторону, в которую направлен
нормальный вектор
по ту сторону, в которую направлен
нормальный вектор![]() и
и![]() если она находится по другую сторону(см. рис. 11).
если она находится по другую сторону(см. рис. 11).

Рис.11.
Разберём задачи на расстояния и отклонения.
Задача
16. Найти
расстояние между плоскостями
![]() и
и![]()
Решение.
Плоскости параллельны, так как их
нормальные векторы
![]() и
и![]() коллинеарны:
коллинеарны:![]() Поэтому расстояние между этими плоскостями
равно расстоянию от какой-нибудь точки
первой плоскости до второй плоскости.
Возьмём точку первой плоскости:
Поэтому расстояние между этими плоскостями
равно расстоянию от какой-нибудь точки
первой плоскости до второй плоскости.
Возьмём точку первой плоскости:![]() Тогда
Тогда
![]()
Задача
17. В
прямоугольном параллелепипеде
![]()
![]()
![]()
![]() Найти расстояние от вершины
Найти расстояние от вершины![]() до плоскости
до плоскости![]()
Решение.
Введём систему координат с началом
![]() как показано на рисунке 12.
как показано на рисунке 12.

Рис.12.
Используя
формулу (4), мы можем записать уравнение
плоскости
![]() “в отрезках”:
“в отрезках”:
![]() (12)
(12)
Нам
требуется найти расстояние от точки
![]() до плоскости, заданной уравнением (12).
Перенесём единицу в левую часть равенства:
до плоскости, заданной уравнением (12).
Перенесём единицу в левую часть равенства:![]() Применим формулу (10):
Применим формулу (10):

Задача
19. Определить,
лежит ли точка
![]() между
плоскостями
между
плоскостями
![]() и
и![]()
Решение.
Обозначим эти плоскости через
![]() и
и![]() Так как плоскости имеют один и тот же
нормальный вектор и не совпадают (это
видно из уравнений плоскостей), то
плоскости параллельны. Вычислим по
формуле (11) отклонения:
Так как плоскости имеют один и тот же
нормальный вектор и не совпадают (это
видно из уравнений плоскостей), то
плоскости параллельны. Вычислим по
формуле (11) отклонения:
![]()
![]()
Так как отклонения одного знака, то точка не лежит между плоскостями (см. рис. 13).

Рис.13.
Задача
20. Даны
плоскости
![]()
![]() и точки
и точки![]()
![]() Определить, точки
Определить, точки![]() и
и![]() лежат внутри одного, смежных или
вертикальных углов, образованных
плоскостями
лежат внутри одного, смежных или
вертикальных углов, образованных
плоскостями![]() и
и![]()
Решение. Вычисляем отклонения:
![]()
![]() –
–
значит,
![]() и
и![]() лежат по одну сторону от плоскости
лежат по одну сторону от плоскости![]()
![]()
![]() –
–
значит,
![]() и
и![]() лежат по разные стороны от плоскости
лежат по разные стороны от плоскости![]() Отсюда следует, что
Отсюда следует, что![]() и
и![]() лежат внутрисмежных
двугранных углов.
лежат внутрисмежных
двугранных углов.
§ 4. Расстояние от точки до прямой в пространстве. Расстояние между скрещивающимися прямыми
Пусть
![]() – прямая с направляющим вектором
– прямая с направляющим вектором![]() и
и![]() – точка прямой
– точка прямой![]() (см. рис. 14).Расстояние
от точки
(см. рис. 14).Расстояние
от точки
![]() до прямой
до прямой![]() выражается
формулой
выражается
формулой
 (13)
(13)

Рис.14.
Пусть
![]() – скрещивающиеся прямые,
– скрещивающиеся прямые,![]() – их направляющие векторы и
– их направляющие векторы и![]() – какие-либо точки, лежащие на прямых
– какие-либо точки, лежащие на прямых![]() соответственно (см. рис. 15).Расстояние
между скрещивающимися прямыми
соответственно (см. рис. 15).Расстояние
между скрещивающимися прямыми
![]() можно вычислить по формуле
можно вычислить по формуле
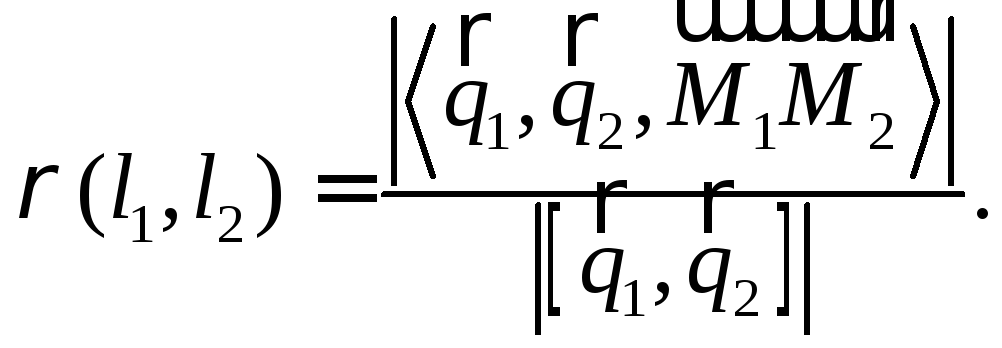 (14)
(14)
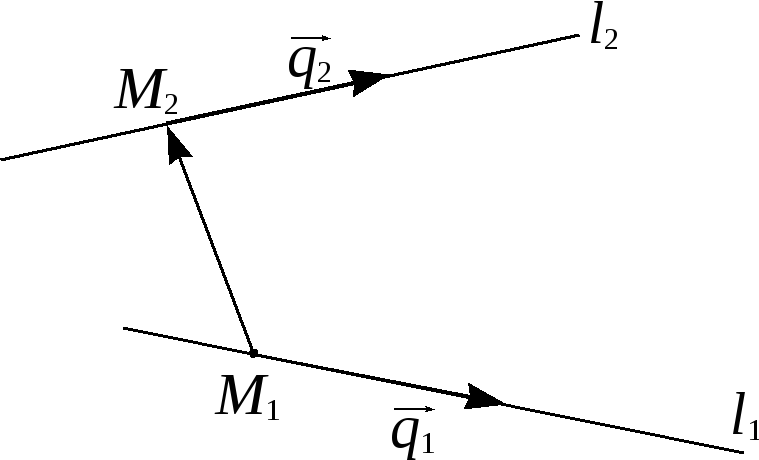
Рис.15.
Замечание.
Если прямые
![]() пересекаются (но не совпадают), то формула
(14) к ним также применима и она показывает,
что расстояние между прямыми равно 0.По формуле
(14) нельзя
вычислять расстояния между параллельными
прямыми.
пересекаются (но не совпадают), то формула
(14) к ним также применима и она показывает,
что расстояние между прямыми равно 0.По формуле
(14) нельзя
вычислять расстояния между параллельными
прямыми.
Задача
21. Найти
расстояние от точки
![]() до прямой
до прямой![]()
Решение.
Из уравнения прямой найдём её направляющий
вектор и точку:
![]() и
и![]() Отсюда
Отсюда![]() По формуле (13) получим:
По формуле (13) получим:

Задача
22. Найти
расстояние между прямыми
![]() и
и![]()
Решение.
Обозначим
данные прямые
![]() и
и![]() Прямые параллельны, они имеют один и
тот же направляющий вектор
Прямые параллельны, они имеют один и
тот же направляющий вектор![]() поэтому формулу (14) применять нельзя.
Применим формулу (13), т.е. найдём расстояние
от точки одной прямой до другой прямой.
Имеем:
поэтому формулу (14) применять нельзя.
Применим формулу (13), т.е. найдём расстояние
от точки одной прямой до другой прямой.
Имеем:![]()
![]() Отсюда
Отсюда![]() по формуле (13) получаем:
по формуле (13) получаем:

Задача
23. Найти
расстояние между прямыми
![]() и
и![]()
Решение.
Обозначим данные прямые
![]() и
и![]() Направляющий вектор прямой
Направляющий вектор прямой![]() равен
равен![]() Прямая
Прямая![]() параллельна оси
параллельна оси![]() поэтому за направляющий вектор этой
прямой можно взять вектор
поэтому за направляющий вектор этой
прямой можно взять вектор![]() Так как
Так как![]() то можно применять формулу (14). В качестве
точек
то можно применять формулу (14). В качестве
точек![]() этих прямых возьмём
этих прямых возьмём![]() и
и![]() По формуле (14) получаем:
По формуле (14) получаем:

Задача
24. Ребро куба
равно
![]() Найти расстояние между скрещивающимися
диагоналями двух смежных граней куба.
Найти расстояние между скрещивающимися
диагоналями двух смежных граней куба.
Решение (см. рис. 16).

Рис.16.
Будем
временно считать, что ребро куба равно
1, затем полученную величину умножим на
![]() Вычислим расстояние между прямыми
Вычислим расстояние между прямыми![]() и
и![]() (другие диагонали дадут такой же
результат). Введём систему координат,
как показано на рисунке. Имеем:
(другие диагонали дадут такой же
результат). Введём систему координат,
как показано на рисунке. Имеем:![]()
![]()
![]()
![]()
![]() Направляющие векторы
Направляющие векторы![]()
![]() прямых равны:
прямых равны:![]()
![]() По формуле (14) получаем:
По формуле (14) получаем:

Следовательно,
![]()
Задача
25. Выяснить
взаимное расположение плоскостей
![]()
![]() и
и![]()
Решение.
Нормальные
векторы этих плоскостей равны:
![]()
![]()
![]() Вычислим их смешанное произведение:
Вычислим их смешанное произведение: Таким образом, векторы
Таким образом, векторы![]() компланарны. Так как никакие два из этих
векторов не коллинеарны, то возможны
следующие варианты взаимного расположения
плоскостей (см. рис. 17): (а) плоскости
попарно пересекаются по трём параллельным
прямым, (б) плоскости проходят через
одну прямую.
компланарны. Так как никакие два из этих
векторов не коллинеарны, то возможны
следующие варианты взаимного расположения
плоскостей (см. рис. 17): (а) плоскости
попарно пересекаются по трём параллельным
прямым, (б) плоскости проходят через
одну прямую.

Рис. 17
Чтобы различить эти две ситуации, решим систему уравнений

Из
первого уравнения
![]() Подставим во второе:
Подставим во второе:![]() откуда
откуда![]() а значит,
а значит,![]() Подставим в третье уравнение:
Подставим в третье уравнение:![]() т.е.
т.е.![]() что невозможно. Таким образом, система
решений не имеет, т.е. плоскости не имеют
общей точки, а значит, имеет место случай
(а).
что невозможно. Таким образом, система
решений не имеет, т.е. плоскости не имеют
общей точки, а значит, имеет место случай
(а).
Задача
26. Составить
уравнение геометрического места точек,
равноудалённых от прямых
![]() и
и![]()
Решение.
Обозначим данные прямые через
![]() и
и![]() Прямые имеют один и тот же направляющий
вектор
Прямые имеют один и тот же направляющий
вектор![]() значит, они параллельны или совпадают.
Возьмём по одной точке этих прямых:
значит, они параллельны или совпадают.
Возьмём по одной точке этих прямых:![]()
![]() Так как
Так как![]() то
то![]() и
и![]() – различные параллельные прямые.
Проведём плоскость
– различные параллельные прямые.
Проведём плоскость![]() через прямые
через прямые![]() и
и![]() в этой плоскости проведём прямую
в этой плоскости проведём прямую![]() посередине между
посередине между![]() и
и![]() а затем через прямую
а затем через прямую![]() проведём плоскость
проведём плоскость![]() перпендикулярную плоскости
перпендикулярную плоскости![]() (см. рис. 18).
(см. рис. 18).

Рис. 18
Очевидно,
плоскость
![]() – это и есть искомое геометрическое
место точек, равноудалённых от прямых
– это и есть искомое геометрическое
место точек, равноудалённых от прямых![]() и
и![]() Нормальным вектором плоскости
Нормальным вектором плоскости![]() может служить вектор
может служить вектор
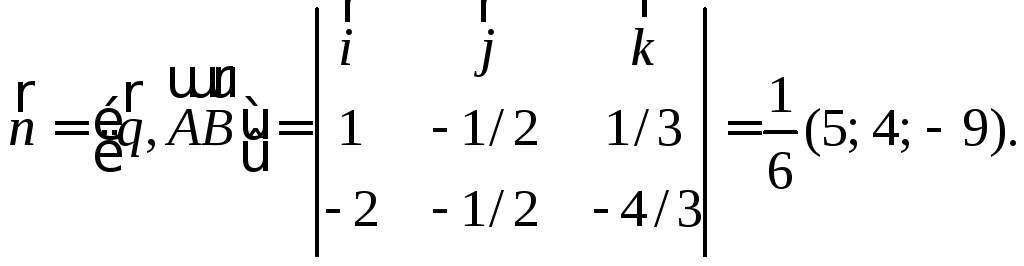
Нормальный
вектор
![]() плоскости
плоскости![]() перпендикулярен векторам
перпендикулярен векторам![]() и
и![]() поэтому можно взять
поэтому можно взять

В
качестве точки плоскости
![]() можно взять точку
можно взять точку![]() – середину отрезка
– середину отрезка![]() Имеем:
Имеем: Подставив в формулу (4), получим:
Подставив в формулу (4), получим:![]() или
или![]()
