§ 3. Полярная, сферическая и цилиндрическая системы координат

П

Рис. 5.31 Рис. 5.32 Рис. 5.33

Рис. 5.34 Рис. 5.35

олярная система координат. Выберем на плоскости точку (полюс) и луч с вершиной(полярную ось) (рис. 5.36). Тогда каждая точка плоскости будет характеризоваться двумя числами:(полярный радиус) – расстояние от точки до полюса и(полярный угол).

П

Рис. 5.36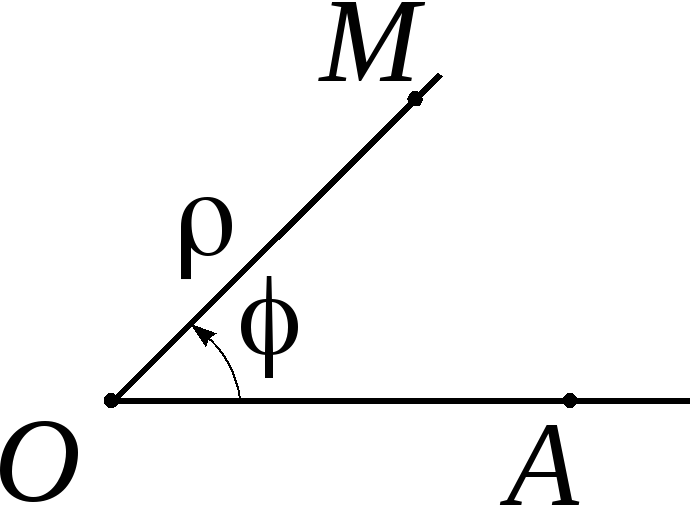

ри этомиЧисланазываютсяполярными координатами точки Используется записьЕдинственная точка, для которой координатане определена, – это полюс. Можно считать значениев полюсе равным любому заданному углу.

Замечание. Иногда считают, что или(в этом случае координатаопределена неоднозначно). Кроме того, в редких случаях разрешается даже неравенство(в этом случае точкаоткладывается не на полярном луче, а на луче, противоположном ему).

П

Рис. 5.37

усть на плоскости взята декартова система координат(рис. 5.37). Примем начало координат за полюс, а осьза полярную ось. Тогда связь между декартовыми и полярными координатами точки будет осуществляться по формулам

Обратные формулы:

при ипри

При можно также написать

Примеры полярных уравнений:

1. – уравнение окружности радиусас центром в полюсе.

2. – уравнение прямой

3. – уравнение кривой второго порядка (эллипса, гиперболы, параболы); здесь– эксцентриситет, полюс расположен в одном из фокусов, полярная ось совпадает с одной из главных осей кривой второго порядка (рис. 5.38).

4

Рис. 5.38 Рис. 5.39

.–трехлепестковая роза (рис. 5.39).

С

Рис. 5.40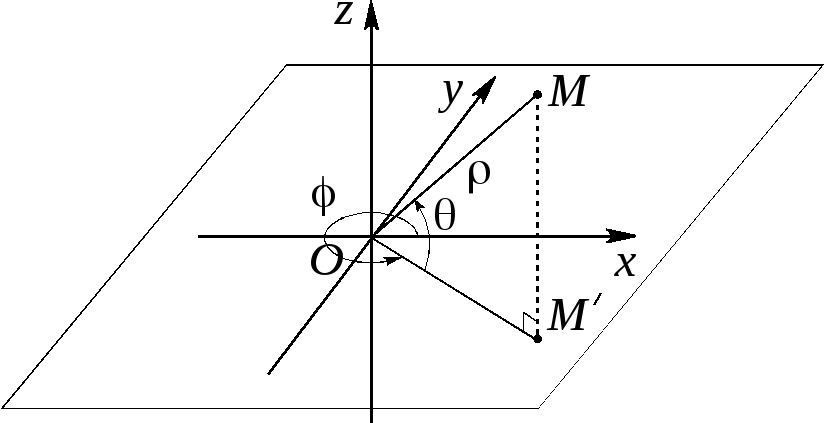

ферическая система координат. Эта система координат вводится для точек пространства.

Опустим перпендикуляр из точкина плоскость(рис. 5.40). Сферическими координатами точкиявляются:– полярный радиус,– угол наклона векторак плоскости(азимут) – угол между осью и векторомПри этом считается, чтоВозможны другие соглашения о диапазоне изменения координат

Связь между декартовыми и сферическими координатами:

Примеры уравнений в сферической системе координат:

1. – уравнение сферы с центром в начале координат.

2. – уравнение конуса. 3.– уравнение цилиндра.

4. – уравнение конуса.

Ц

Рис. 5.41

илиндрическая система координат занимает промежуточное положение между декартовой и сферической системами. Цилиндрическими координатами точки пространства являются полярные координатыпроекции точкина плоскостьи аппликататочки(рис. 5.41).

Связь между декартовыми и цилиндрическими координатами точки:

Примеры уравнений поверхностей в цилиндрической системе координат:

1. – уравнение конуса.

2. – уравнение цилиндра.

3. Пусть на плоскости дан круг радиусас центром на осипричем центр круга находится на расстоянииот начала координат (см. рис. 5.42). Тело, полученная вращением круга вокруг осиносит названиетор (см. рис. 5.43).

Так как уравнение окружности на плоскости имеет вид

§ 4. Поверхности

Поверхности задаются обычно уравнением вида или, если удастся выразитьчерези– уравнением видаНапример, сфера (поверхность шара) задается уравнениемгде– центр шара,– его радиус. Выражаячерезиполучим две поверхности:верхнюю полусферу инижнюю полусферу