МП-1 / Коллоквиум 1 поток / Новая папка / 3 Проекция вектора на вектор

Скалярный квадрат вектор

А что будет, если вектор  умножить на самого себя? Понятно, что вектор сонаправлен сам с собой поэтому или 

Число  называется скалярным квадратом вектора 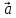, и обозначатся как 

Таким образом, скалярный квадрат вектора  равен квадрату длины данного вектора:Из данного равенства можно получить формулу длины вектора:

Угол между векторами

Снова посмотрим на нашу формулу  .По правилу пропорции Скалярное произведение  и длины векторов  – числа. Значит,  тоже является числом. А если известен косинус угла:  , то с помощью обратной функции легко найти и сам угол:  ,.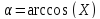

Проекция вектора на вектор. Проекция вектора на координатные оси.  Направляющие косинусы вектора

Рассмотрим векторы  и :

Если угол между векторами  острый (как на рисунке), то

Если векторы  ортогональны, то  (проекцией является точка, размеры которой считаются нулевыми).

Если угол между векторами  тупой (на рисунке мысленно переставьте стрелочку вектора ), то  (та же длина, но взятая со знаком минус).

Отложим данные векторы от одной точки:

Очевидно, что при перемещении вектора его проекция не меняется

Рассмотрим прямоугольный треугольник. Косинусом острого угла называется отношение прилежащего катета к гипотенузе. В данном случае:

С другой стороны, у нас уже получена формула косинуса угла между векторами:

Таким образом: Или