МП-1 / Коллоквиум 1 поток / Новая папка / 18.Вывод канонических уравнений а) эллипса, б) гиперболы, в) параболы

Вывод канонических уравнений

А) Эллипс

Определение. Эллипс – геометрическое множество точек М в плоскости, таких что:

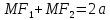
M(x,y)

Точки F₁ и F₂ называются фокусами эллипса.

F₁

F₂

Вывод канонического уравнения:

Пусть координаты точек: F₁ = (-c; 0)

F₂ = (c; 0)

M = (x; y)

Возведем обе части уравнения в квадрат:

Возведем полученное уравнение в квадрат:

Пусть , тогда:

Поделим обе части равенства на , получим:

где a – большая полуось, b – меньшая полуось.

Б) Гипербола

Определение. Гипербола – геометрическое место точек, разность расстояний от которых до двух заданных точек F₁ и F₂ постоянна.

Точки F₁ и F₂ называются фокусами гиперболы.

Вывод канонического уравнения:

Пусть координаты точек: F₁ = (-c; 0)

F₂ = (c; 0)

M = (x; y)

Возведем обе части уравнения в квадрат:

Возведем полученное уравнение в квадрат:

Пусть , тогда:

Поделим обе части равенства на , получим:

В) Парабола

Определение. Парабола – множество точек М такое, что

где точка F – фокус параболы, прямая d – директриса (направляющая).

Вывод уравнения:

Пусть F = (p/2; 0)

d: x = -p/2

Получим: