Упражнения.

1. Найти все матрицы, перестановочные с данной:

а) ; б) .

2. Найти все матрицы второго порядка, квадраты которых равны нулевой матрице.

3. Доказать, что .

Упражнения. Доказать следующие свойства обратной матрицы.

1. Если , то .

2. .

3. .

Упражнение. Найти ранг матрицы методом окаймляющих миноров и методом элементарных преобразований:

.

Упражнения. Решить методом Гаусса следующие системы уравнений:

1. 2.

3.

Упражнения

1. Доказать, что множество всех геометрических векторов является линейным пространством.

2. Пусть - множество всех упорядоченных наборов чисел вида . Пусть и . Положим . Пусть - произвольное действительное число, положим . Доказать, что - линейное пространство ( называют линейным пространством -мерных арифметических векторов).

3. Доказать, что множество непрерывных на отрезке функций является линейным пространством.

Упражнение. Доказать, что в линейном пространстве 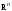система векторов , , …, 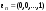является базисом.

Упражнения.

1. - линейное пространство многочленов степени . Доказать, что система многочленов образует базис в . Найти матрицу перехода от базиса к этому базису и координаты многочлена в нем.

2. В произвольном линейном пространстве векторы и заданы своими координатами в некотором базисе : , , , . Доказать, что система векторов - базис в , и найти координаты в этом базисе.

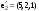3. В произвольном линейном пространстве векторы (I) и (II) заданы своими координатами в некотором базисе , , , , , . Доказать, что системы (I) и (II) являются базисами в , и найти матрицу перехода от (I) к (II).

Упражнение. - линейное пространство арифметических векторов . Найти размерность и все базисы линейной оболочки векторов , , , .

Упражнения.

1. - линейное пространство всех многочленов степени , - оператор дифференцирования, . Доказать, что - линейный оператор.

2. - линейное пространство всех непрерывных на отрезке функций. Для любой оператор определен следующим равенством:

, .

Доказать, что - линейный оператор.

Упражнение. - линейное пространство всех геометрических векторов, 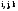- декартов базис, - декартова система координат, - оператор проектирования на ось . Доказать, что - линейный оператор, и найти его матрицу в базисе .

Упражнение. - линейное пространство всех геометрических векторов плоскости, - декартов базис, - декартова система координат, - оператор поворота плоскости вокруг начала координат на угол против часовой стрелки. Доказать, что - линейный оператор, найти матрицу оператора в базисе и координаты образа вектора .

Упражнение. - линейное пространство всех геометрических векторов, - линейный оператор проектирования на ось . Найти все его собственные числа и собственные векторы.

Упражнения.

1. Пусть и - произвольные векторы пространства арифметических векторов . Показать, что скалярное произведение в можно определить следующими способами:

а) ; б) .

Вычислить скалярное произведение векторов и каждым из указанных способов.

2. Доказать, что в пространстве соотношение

задает скалярное произведение. Написать неравенство Коши - Буняковского для этого пространства.

Упражнения.

1. Проверить ортогональность системы векторов и в евклидовом пространстве и дополнить ее до ортогонального базиса.

2. Применяя процесс ортогонализации Шмидта, построить ортогональный базис в линейной оболочке системы векторов , , , .

Упражнения.

1. Указать какой-нибудь ортонормированный базис в линейной оболочке векторов , , , .

2. - евклидово пространство геометрических векторов. Построить какой-нибудь ортонормированный базис в линейной оболочке векторов , и .

Упражнения.

Доказать следующие свойства ортогональной матрицы.

1. Если - ортогональная матрица, то .

2. Если - ортогональная матрица, то тоже ортогональная.

3. Если - ортогональная матрица, то тоже ортогональная.

4. Матрица является ортогональной в том и только в том случае, когда ее строки составляют ортонормированную систему арифметических векторов.