Билет 10. Правило Крамера.

Пусть дана система линейных алгебраических уравнений снеизвестными:

(9.1)

Обозначим ,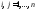.будем называть определителем системы (9.1).

Обозначим ,. Система (9.1) равносильна матричному уравнению

. (9.2)

Теорема 1. Если , то система (9.1) имеет, притом единственное, решение.

Доказательство. Так как, то. Умножим обе части (9.2) наслева:

.

Итак, решением матричного уравнения (9.2) является матрица - матричное уравнение (9.2) имеет решение, следовательно, система (9.1) совместна.

(9.3)

Решение системы (9.1) дается формулами (9.3), и так как ,, вполне определенные числа, единственно.

Теорема доказана.

Правило Крамера:если , то решение системы (9.1) может быть найдено по формулам , , где- определитель, который получится из, если столбец коэффициентов при заменить столбцом свободных членов.

Пример 1.По правилу Крамера, если оно применимо, решить систему

Решение.Имеем

,

следовательно, правило Крамера применимо.

,

,

.

По формулам (9.3) находим

, ,.

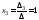Билет 11. Теорема Кронекера-Капелли.

Пусть дана система уравнений снеизвестными:

(9.4)

Обозначим матрицу из коэффициентов

.

Матрица содержит матрицуи еще столбец свободных членов, она называетсярасширеннойматрицей по отношению к:

.

Теорема 2 (Кронекера - Капелли).Система совместна тогда и только тогда, когда .

Доказательство. Необходимость. Пусть система (9.4) совместна и- решение (9.4), следовательно, справедливы тождества

(9.5)

В матрице к последнему столбцу прибавим первый, умноженный на, второй, умноженный на,…,-й, умноженный наПолучим, учитывая (9.5),

~.

Поскольку выполнялись элементарные преобразования, то , но(добавление столбца из нулей не может изменить ранга), отсюда

.

Достаточность.Пусть. Это означает, что существует минорпорядка, а все миноры порядка, окаймляющие, равны нулю.

Пусть расположен в левом верхнем углу матрицы(это предположение не ограничивает общности рассуждений, так как можно переставить уравнения и перенумеровать неизвестные и тем самым добиться того, чтобудет расположен в первыхстроках и первыхстолбцах матрицы):

.

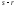Тогда первые строк матрицы линейно независимы, а остальныестрок являются их линейной комбинацией (теорема о базисном миноре), следовательно, через первыеуравнений линейно выражаются остальныеуравнений. Таким образом, вся система (9.4) эквивалентна первымуравнениям:

(9.6)

Случай 1:. Система (9.6) имеет единственное решение (определитель системы (9.6), - применяем теорему 1). Его можно найти, например, по правилу Крамера.

Случай 2:. Перепишем (9.6) в виде

(9.7)

Неизвестные назовем главными,- свободными.

Присвоим свободным неизвестным произвольные числовые значения, положим . Тогда согласно теореме 1 из системы (9.7) определится единственный наборглавных неизвестных. Таким образом, наборчисел,является решением системы (9.4).

Значения свободных неизвестных можно выбрать бесчисленным множеством способов, поэтому система (9.4) имеет бесчисленное множество решений.

И в случае 1, и в случае 2 система оказалась совместной. Достаточность доказана.

Определение 1.Формула, выражающая решение системы (9.4) в виде вектор-функции свободных неизвестных, называется общим решением системы (9.4):

.

Пример 2.Исследовать совместность системы и, если система совместна, найти общее решение и одно частное:

Решение.Найдем ранг матрици:

~~

~.

Итак, (минор второго порядка, все миноры, его окаймляющие, равны нулю и в, и в). Следовательно, согласно теореме 2 система совместна.

Так как , система имеет бесчисленное множество решений.

Вся система эквивалентна системе первых двух уравнений:

В качестве главных неизвестных возьмем и(), свободных -ии перепишем систему в виде

-

"укороченная" система.

Отсюда

и .

Общее решение

.

Частное решение получим, присвоив конкретные числовые значения свободным неизвестным, например, , тогда

.