Билет 4. Умножение матриц, свойства умножения (доказать дистрибутивность).

Определение 8. Произведением матрицы 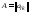, , , на матрицу , , , называется матрица , , , с элементами .

Краткая запись: .

Пример 10. Найти произведение матриц

и .

В соответствии с определением 8 найдем

.

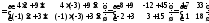Пример 11. Перемножить матрицы

и .

Имеем

.

Замечание 1. Число элементов в строке матрицы равно числу элементов в столбце матрицы(число столбцов матрицыравно числу строк матрицы).

Замечание 2. В матрице строк столько же, сколько в матрице, а столбцов столько же, сколько в.

Замечание 3. Вообще говоря, (умножение матриц некоммутативно).

Чтобы обосновать замечание 3, достаточно привести хотя бы один пример.

Пример 12. Перемножим в обратном порядке матрицы ииз примера 10.

,

таким образом, в общем случае .

Отметим, что в частном случае равенство возможно.

Матрицы и, для которых выполняется равенство, называютсяперестановочными, или коммутирующими.

Свойства умножения матриц:

1. Умножение дистрибутивно:

, .

2. Умножение ассоциативно: .

Докажем свойство 1. Пусть ,,,,,,,,.

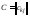Обозначим ,,,,,,,.

Имеем

,

и, таким образом, в соответствии с определением 6 , или, возвращаясь к старым обозначениям,. Свойство 1 доказано.

Так как умножение матриц некоммутативно, следовало бы доказать и правую дистрибутивность: . Опустим доказательство, так как оно аналогично приведенному доказательству левой дистрибутивности.

Докажем свойство 2. Пусть ,,,,,,,,.

Обозначим ,,,,,,,,,,,.

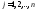Имеем

,

таким образом, .

Вернемся к старым обозначениям и получим: , т.е. свойство 2 доказано.

Для квадратных матриц справедливо следующее утверждение, которое приведем без доказательства.

Теорема 2. Для любых двух квадратных матриц и

.

Приведем пример, иллюстрирующий утверждение теоремы 2.

Пример 13. Даны матрицы

и .

Вычислить .

Воспользуемся теоремой 2: .

Найдем произведение непосредственно:

. Следовательно, результаты совпадают.

Билет 5. Обратная матрица, существование и единственность.

Далее будут рассматриваться квадратные матрицы.

Единичная матрица

в умножении квадратных матриц порядка играет роль, аналогичную роли числа единица в умножении чисел:

. (7.1)

Действительно, пусть

.

Непосредственная проверка дает: . Аналогично, и равенство (7.1) справедливо.

Утверждение 1. Матрица - единственная матрица, обладающая свойством (7.1).

Доказательство. Пусть такая, что

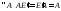. (7.2)

Рассмотрим произведение :

.

Определение 1. Пусть - произвольная квадратная матрица. Матрицаназывается правой обратной для, если . Матрицаназывается левой обратной для, если .

Определение 2. Квадратная матрица называется вырожденной (особенной), если , и невырожденной (неособенной), если .

Утверждение 2. Вырожденная матрица не имеет ни правой, ни левой обратной.

Доказательство. Пусть - вырожденная. Допустим,- правая обратная для, т.е..

Тогда , но, что является противоречием, следовательно,не имеет правой обратной.

Аналогично доказывается, что не имеет и левой обратной.

Утверждение 3. Пусть - произвольный определитель порядка. Сумма произведений всех элементов любого столбца(строки) на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю.

Доказательство. Пусть

.

В силу теоремы о разложении по строке (лекция 6, теорема 1) имеем

,

где - алгебраическое дополнение к элементу.

Пусть - произвольные вещественные числа. Рассмотрим сумму.

Привлекая ту же теорему о разложении по строке, можем записать

.

Возьмем в качестве чисел ,, элементы-го столбца определителя,, тогда

Утверждение 3 доказано.

Перейдем к построению обратной матрицы методом присоединенной. Пусть - невырожденная матрица порядка:

.

Матрица

называется присоединенной для . Элементами матрицыявляются алгебраические дополнения к элементам матрицы, причем алгебраические дополнения к элементамi-й строки матрицы помещены вi-й столбец .

Обозначим .

Матрица является правой и левой обратной для.

Действительно,

Следовательно, матрица - правая обратная для. Аналогично, и матрицаявляется и левой обратной для. Она называетсяобратной для и обозначается.

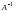Итак,

.

Утверждение 4. Матрица - единственная обратная для.

Действительно, допустим, такая, что.

Рассмотрим . С другой стороны,, следовательно,.

Пример 1. Найти для матрицы.

Решение. Имеем , следовательно,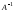существует.

Найдем алгебраические дополнения к элементам матрицы и составим присоединенную матрицу:

.

Откуда .