Билет 35. Положительно определенные квадратичные формы. Критерий Сильвестра.

Определение 5. Нормальным видом квадратичной формы называется сумма квадратов неизвестных с коэффициентами «+!» или «».

Теорема 4. Всякую квадратичную форму можно привести некоторым невырожденным линейным преобразованием неизвестных к нормальному виду.

Доказательство. Пусть - квадратичная форма ранга. Следовательно,- линейное преобразование неизвестных, приводящеек виду

, (14.20)

где 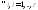,(теорема 3 и следствие из теоремы 2).

Положим

(14.21)

Равенства (14.21) можно записать в виде следующего матричного равенства:

,

где - невырожденная матрица (так как 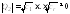), следовательно, существуети равенствоможно разрешить относительно:.

Последовательное выполнение линейных преобразований и является линейным преобразованием с матрицей(теорема 1); линейное преобразованиеприводит квадратичную формук нормальному виду

.

Теорема 4 доказана.

Определение 6. Квадратичная форма от n неизвестных называется положительно определенной, если она приводится к нормальному виду, содержащему n квадратов неизвестных с коэффициентами «+1»:

Теорема 5. Квадратичная форма является положительно определенной тогда и только тогда, когда при любых значениях неизвестных, хотя бы одно из которых отлично от нуля, эта форма принимает положительные значения.

Доказательство. Пусть положительно определена, т.е. приводится некоторым невырожденным линейным преобразованиемк виду

.

Так как - невырожденная матрица, и. Пусть , , тогда

(14.22)

Пусть - набор неизвестных, среди которых хотя бы одно отлично от нуля. Следовательно, в равенствах (14.22) среди соответствующих значений найдется. Действительно, допустим,. Тогда система линейных алгебраических уравнений

с определителем имеет единственное решение , а по условию хотя бы одно из неизвестных,, отлично от нуля, получили противоречие и, следовательно, среди,, есть. Тогда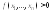(так как).

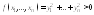Обратно. Пусть . Допустим, чтоне является положительно определенной, - это означает, что в нормальном виде, к которому приводится квадратичная форманекоторым невырожденным линейным преобразованием, либо отсутствует квадрат хотя бы одного неизвестного, либо входит с коэффициентом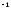. Пусть это неизвестное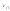. Тогда, либо.

Рассмотрим следующий набор неизвестных :

, . (14.23)

Пусть неизвестные ,, связаны с,, равенствами (14.22). Набор неизвестных, соответствующий (14.23), найдем из системы уравнений

(14.24)

Пусть - решение системы (14.24), следовательно,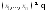, так как если, не удовлетворяется, например, последнее уравнение в (14.24).

Имеем

и, таким образом, , получили противоречие, и, значит, нормальный вид квадратичной формы содержитквадратов неизвестных с коэффициентами +1 иявляется положительно определенной формой.

Теорема 5 доказана.

Определение 7. Пусть, ,.Миноры , , ,…, называются главными минорами квадратичной формы .

Сформулируем без доказательства следующее утверждение.

Теорема 6 (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все ее главные миноры строго положительны.