Билет 1. Определение определителя порядка n, его свойства.

Определение 1.Матрицей называется прямоугольная таблица чисел.

Для обозначения матрицы используются круглые скобки или сдвоенные вертикальные линии:

.

Числа, составляющие матрицу, называются ее элементами, элементматрицырасположен в ее-й строке и-м столбце.

Числа и(число строк и столбцов матрицы) называются ее порядками.

Говорят также, что - матрица размером.

Если , матрицаназываетсяквадратной.

Для краткой записи используется также обозначение (или) и далее указывается, в каких пределах изменяютсяи, например,,,. (Запись читается так: матрицас элементами,изменяется отдо,- отдо.)

Среди квадратных матриц отметим диагональные матрицы, у которых все элементы с неравными индексами () равны нулю:

.

Будем говорить, что элементы расположены на главной диагонали.

Диагональная матрица вида

называется единичнойматрицей.

В дальнейшем будут встречаться матрицы вида

и ,

которые называются треугольнымиматрицами, а также матрицы, состоящие из одного столбца:

и одной строки:

(матрица-столбец и матрица-строка).

Матрица, все элементы которой равны нулю, называется нулевой.

6.2. Определители порядка n

Пусть дана квадратная матрица порядка :

. (6.1)

Составим всевозможные произведения элементов матрицы, расположенных в разных строках и разных столбцах, т.е. произведения вида

. (6.2)

Число произведений вида (6.2) равно (примем этот факт без доказательства).

Будем считать все эти произведения членами определителя порядка , соответствующего матрице (6.1).

Вторые индексы множителей в (6.2) составляют перестановку первых натуральных чисел.

Говорят, что числа ив перестановке составляютинверсию, если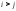, а в перестановкерасположено раньше.

Определение 2.Определителем порядка , соответствующим матрице (6.1), называется алгебраическая сумма членов, составленная следующим образом: членами определителя служат всевозможные произведения элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем слагаемое берется со знаком "+", если множество вторых индексов является четной перестановкой чисел , и со знаком "–", если нечетной.

Обозначать определитель матрицы (6.1) принято так:

.

Замечание.Определение 2 для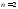иприводит к уже знакомым нам определителям 2-го и 3-го порядка:

,

.

Транспонированием вокруг главной диагонали матрицыназывается переход к матрице, для которой строки матрицыявляются столбцами, а столбцы - строками:

.

Будем говорить, что определитель получен транспонированием определителя.

Свойства определителя порядка п:

1. (определитель не меняется при транспонировании вокруг главной диагонали).

2. Если одна из строк определителя состоит из нулей, определитель равен нулю.

3. От перестановки двух строк определитель меняет лишь знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на число , определитель умножится на.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы -й строки определителя представлены в виде суммы, то определитель равен сумме двух определителей, у которых все строки, кроме-й, такие же, как в исходном определителе, а-я строка в одном определителе состоит из, а в другом - из.

Определение 3.-я строка определителя называется линейной комбинацией остальных его строк, если такие, что, умножая -ю строку на, а затем складывая все строки, кроме -й, получаем -ю строку.

8. Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю.

9. Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число.

Замечание.Мы сформулировали свойства определителя для строк. В силу свойства 1 () они справедливы и для столбцов.

Все приведенные свойства были доказаны на практических занятиях для ; для произвольногопримем их без доказательства.

Если в определителе порядкавыбрать элементи вычеркнуть столбец и строку, на пересечении которых расположен, оставшиеся строки и столбцы образуют определитель порядка, который называетсяминором определителя, соответствующим элементу.

Определение 4.Алгебраическим дополнением элементаопределителяназывается его минор, умноженный на , где - номер строки, - номер столбца, в которых расположен выбранный элемент .

Теорема 1 (о разложении по строке).Определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения.

Теорема 1 позволяет свести вычисление определителя порядка к вычислениюопределителей порядка.

Замечание.Можно вначале упростить определитель, воспользовавшись свойством 9, а затем использовать теорему 1. Тогда вычисление определителя порядкасведется к вычислениювсего одногоопределителя порядка.

Замечание.Определитель треугольного вида равен произведению элементов главной диагонали.