discretka_2 / lect12_m2_vm1_ipovs_DM_231000.62

Лекция 12

§ 3.4. Планарность

Укладки графа в пространстве и на плоскости. Планарные графы. Плоские графы. Грани плоского графа. Связь между числом вершин, ребер и граней плоского графа, формула Эйлера. Критерии планарности.

Базовые понятия и утверждения

1. Укладка графа в трехмерном пространстве. Говорят, что граф обладает укладкой в пространстве, если в трехмерном евклидовом пространстве можно построить такую диаграмму графа, в которой ребра не имеют общих точек, отличных от концевых. Сама диаграмма, обладающая указанным свойством, называется при этом укладкой графа в пространстве.

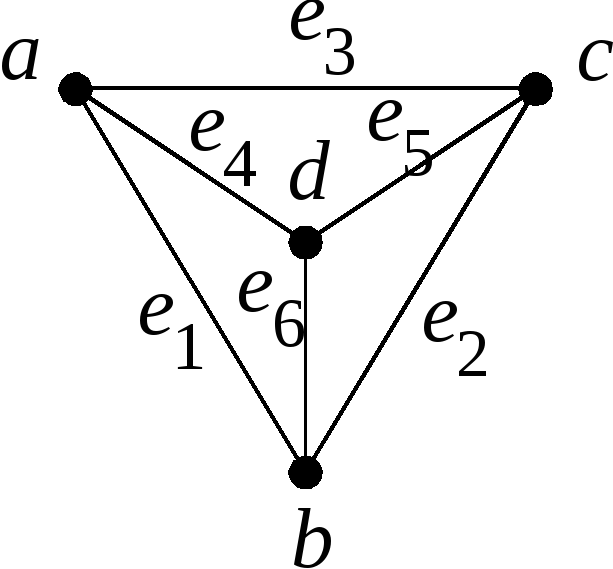
Пример 1. Рассмотрим граф с вершинами , , , и ребрами , , , , , .

Укладка данного графа в пространстве изображена на рис. 3.48.

Утверждение. Любой граф обладает укладкой в пространстве.

Доказательство. Покажем, как в трехмерном евклидовом пространстве построить укладку для произвольного графа.

Возьмем в пространстве любую прямую (рис. 3.49). Вершинам графа поставим в соответствие точки прямой так, чтобы каждой вершине соответствовала своя точка; каждую точку пометим именем сопоставленной ей вершины.

Рис. 3.48.	Рис. 3.49.

Через прямую проведем столько плоскостей, сколько ребер у графа (каждому ребру будет соответствовать своя плоскость). Если ребро не является петлей, то изобразим его в соответствующей ему плоскости в виде полуокружности с диаметром . Если ребро - петля, то изобразим его в соответствующей ему плоскости в виде окружности, которая касается прямой в точке .

Очевидно, построенная таким образом диаграмма будет укладкой графа в трехмерном пространстве. ■

2. Планарные графы. Говорят, что граф обладает укладкой на плоскости, если в двумерном евклидовом пространстве существует такая диаграмма графа, в которой ребра не имеют общих точек, отличных от концевых.

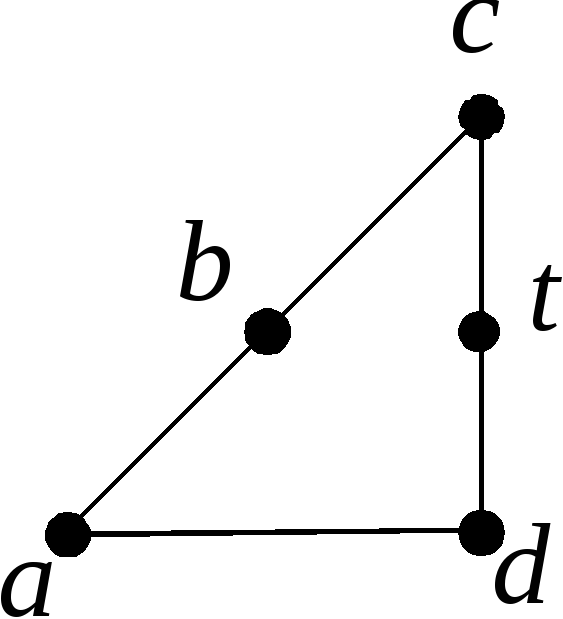
На рис. 3.50 изображена укладка на плоскости графа из примера 1.

Далее мы убедимся в том, что не все графы имеют плоскую укладку. Граф, обладающий укладкой на плоскости, называют планарным. Любую укладку планарного графа на плоскости называют плоским графом.

Например, граф из примера 1 - планарный, а его диаграмма на рис. 3.50 - плоский граф.

Совокупность ребер каждого простого цикла плоского графа может рассматриваться как граница некоторой области на плоскости. Те из этих областей, которые не содержат внутри себя ребер других простых циклов данного плоского графа, называют гранями плоского графа.

Отметим, что одна из граней любого плоского графа не ограничена. Ее называют внешней гранью, остальные грани называют внутренними гранями.

Например, плоский граф, изображенный на рис. 3.51, имеет четыре грани: три внутренние (, , ) и одну внешнюю (). Любое дерево имеет только одну грань - внешнюю.

Рис. 3.50.	Рис. 3.51.

Справедливо следующее утверждение.

Пусть - связный плоский граф, - множество его граней. Тогда (формула Эйлера).

Доказательство утверждения приведено во второй части параграфа.

Чтобы доказать планарность графа, достаточно нарисовать его плоскую укладку. Непланарность графов обосновывать сложнее (ссылки на тщетность попыток нарисовать плоскую укладку графа доказательством не являются). В некоторых случаях непланарность удается доказать с помощью формулы Эйлера.

Пример 2. Доказать, что полный граф непланарен.

◄ Будем рассуждать от противного. Предположим, что граф (см. рис. 3.7) планарен. Тогда у него есть укладка на плоскости. Пусть - множество граней этой укладки и граница i-й грани состоит из ребер, где . Поскольку каждое ребро графа содержится в некотором цикле и, следовательно, лежит на границе двух граней, то

.

Граф не имеет петель и кратных ребер, значит, каждая грань его укладки граничит не менее чем с тремя ребрами и . Следовательно, , т.е. . Граф имеет 5 вершин и 10 ребер, следовательно, по формуле Эйлера . Значит, должно выполняться неравенство , что неверно. Пришли к противоречию. Следовательно, предположение о планарности графа было неверным. ►

Пример 3. Доказать, что полный двудольный граф непланарен.

◄ Будем рассуждать от противного. Предположим, что граф (см. рис. 3.8) планарен. Пусть - множество граней этой укладки и граница i-й грани состоит из ребер, где . Поскольку каждое ребро графа содержится в некотором цикле и, следовательно, лежит на границе двух граней, то

.

Несложно убедиться, что в графе все простые циклы имеют длину, не меньшую 4, т.е. (), и, значит, , откуда . С учетом того, что граф имеет 6 вершин и 9 ребер по формуле Эйлера получим , значит, должно выполняться неравенство . Пришли к противоречию. Следовательно, предположение о планарности графа было неверным. ►

Теоретические обоснования

Теорема 3.5 (о плоских графах). Пусть - плоский граф, - множество его граней. Тогда

.

Доказательство. Доказательство проведем по индукции, взяв в качестве параметра число ребер графа.

Базис индукции. Пусть , т.е. граф не имеет ребер. Тогда , , поэтому доказываемая формула справедлива.

Индуктивный переход. Предположим, что формула верна для любого графа с числом ребер, меньшим либо равным . Покажем, что она остается в силе для графа , число ребер которого равно . Возьмем какое-нибудь ребро графа и удалим его. Получим граф , число ребер которого равно . Тогда для плоской укладки графа справедливо предположение индукции и, значит, выполняется равенство

.

Рассмотрим два случая: 1) удаленное ребро - не мост и 2) удаленное ребро - мост.

1. Пусть удаленное ребро - не мост. Тогда содержится в некотором цикле графа и поэтому лежит на границе двух граней его плоской укладки. Если удалить из графа ребро , то эти две грани сольются в одну и число граней в плоской укладке графа окажется на единицу меньшим числа граней в плоской укладке графа , т.е. .

Из того, что - не мост, следует также, что . Кроме того, , .

Следовательно, равенство

можно переписать в виде

или

.

2. Пусть теперь удаленное ребро - мост. Тогда не содержится ни в одном цикле графа и поэтому не входит в границы граней плоской укладки этого графа. Значит, ни одна из граней графа не пострадает при его удалении, так что . Из того, что - мост следует также, что . Кроме того, , .

Следовательно, равенство

можно переписать в виде

,

или

.

Таким образом, в обоих случаях индуктивный переход доказан. ■

Заметим, что поскольку , то из теоремы следует, что цикломатическое число плоского графа равно числу его внутренних граней.

Следствие. В частном случае связного плоского графа из равенства получаем формулу Эйлера .

Будем говорить, что граф получен из графа включением вершины степени 2, если в графе одно из ребер (равенство не исключается) заменено на два новых ребра и , где - новая вершина степени 2, а остальные вершины и ребра остались без изменения.

Операция, обратная операции включения вершины степени 2, называется исключением вершины степени 2.

Будем говорить, что граф гомеоморфен графу , если изоморфен некоторому графу, который можно получить из путем применения конечное число раз операций включения и исключения вершин степени 2.

Пример 4. Графы , и (рис. 3.54) - попарно гомеоморфны. Действительно, граф можно получить из графа путем исключения вершины (и наоборот, граф можно получить из графа путем включения вершины ). Граф можно получить из графа путем включения вершины (и наоборот, граф можно получить из графа путем исключения вершины ). Граф можно получить из графа путем включения вершин и (и наоборот, граф можно получить из графа путем исключения вершин и ).

Рис. 3.54.

Приведем без доказательства один из критериев планарности.

Теорема 3.6 (Понтрягина и Куратовского). Граф планарен тогда и только тогда, когда у него нет подграфов, гомеоморфных , и нет подграфов, гомеоморфных .

Пример 5. На рис. 3.55 изображены граф Петерсена и его подграф .

Рис. 3.55.

Граф гомеоморфен графу . Это следует из того, что граф изоморфен графу (на рис. 3.55 соответствующие вершины помечены одинаковыми числами), а граф гомеоморфен графу . Таким образом, граф Петерсена непланарен. Заметим, что при этом граф Петерсена не содержит подграфов, гомеоморфных .

Теперь определим на графе операцию стягивания ребра. Пусть - ребро графа , не являющееся петлей. Последовательно выполним следующие действия: отождествим вершины и , отождествим возникшие при этом кратные ребра и отбросим все возникшие при этом петли. Обозначим полученный граф . Будем говорить, что граф получен из графа стягиванием ребра .

Пример 6. На рис. 3.56 показан пример применения операции стягивания ребра: граф получен из графа стягиванием ребра .

Рис. 3.56.

Будем говорить, что граф стягиваем к графу , если можно получить из с помощью конечного числа применений операции стягивания ребер.

Приведем без доказательства еще один критерий планарности.

Теорема 3.7 (Вагнера, Харари и Татта). Граф планарен тогда и только тогда, когда у него нет подграфов, стягиваемых к , и нет подграфов, стягиваемых к .

Пример 7. Граф Петерсена непланарен, поскольку он стягиваем к графу . Действительно, получается из графа Петерсена путем последовательного стягивания ребер с концами 1 и 5, 6 и 9, 2 и 7, 4 и 8, 3 и 10 (см. рис. 3.55).

8