Лекция 15

§ 3.10. Задача о максимальном потоке в сети

Сеть. Поток в сети. Величина потока. Максимальный поток. Дополняющая цепь. Разрез в сети. Минимальный разрез. Алгоритм Форда - Фалкерсона.

Базовые понятия и утверждения

В этом параграфе будут рассматриваться сети , имеющие единственную вершину с нулевой полустепенью захода и единственную вершину с нулевой полустепенью исхода. Вершину будем называть источником, а вершину - стоком, вес дуги - пропускной способностью дуги .

Для удобства изложения введем следующие обозначения. Через обозначим множество дуг, для которых вершина является началом, а через обозначим множество дуг, для которых вершина является концом.

Определение. Потоком в сети называется функция , удовлетворяющая условиям:

1) ;

2) для всех вершин , , , где и .

Значение можно интерпретировать как поток, втекающий в вершину , а значение - как поток, вытекающий из вершины . Тогда второе условие можно переформулировать так: поток, втекающий в любую вершину, за исключением источника и стока, должен быть равен потоку, вытекающему из этой вершины.

Условие 1) называется условием ограничения по пропускной способности, а условие 2) - условием сохранения потока в вершинах.

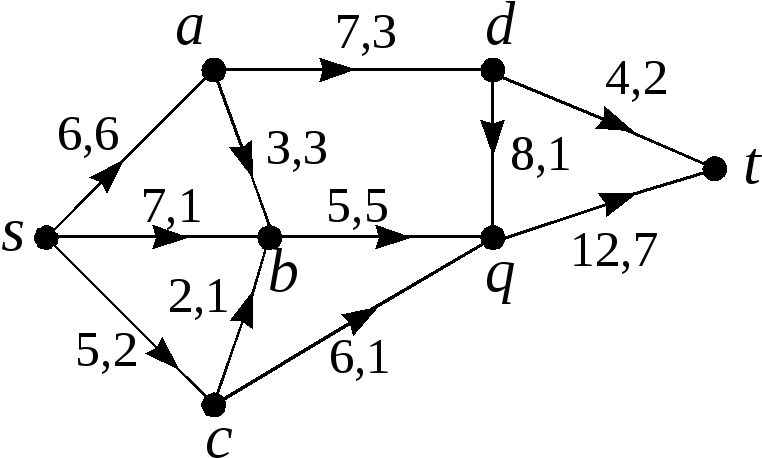
Рис. 3.83.

Пример 1. На рис. 3.83 дан пример сети и потока в ней.

Около каждой дуги указаны через запятую ее пропускная способность и текущий по ней поток .

Определение. Положим . Число называется величиной потока.

Определение. Поток называется максимальным, если для любого потока справедливо неравенство .

Задача о максимальном потоке формулируется следующим образом: в заданной сети найти поток максимальной величины.

Задача о максимальном потоке имеет особенность, отличающую ее от рассмотренных нами ранее задач дискретной оптимизации. В предшествующих задачах искомый объект существовал очевидным образом и в принципе мог быть найден полным перебором. Например, можно было перебрать все остовы и выбрать среди них минимальный или перебрать все пути между заданными вершинами и выбрать среди них кратчайший. В задаче о максимальном потоке полный перебор принципиально невозможен и существование максимального потока не является очевидным. Однако можно доказать, что в каждой сети существует максимальный поток (доказательство этого утверждения опустим).

При решении задачи об отыскании максимального потока в сети приходится рассматривать неориентированные простые цепи, т.е. такие последовательности попарно различных вершин и дуг , в которой любые два соседних элемента инцидентны. Поскольку цепи других видов нас при этом интересовать не будут, то далее в этом параграфе неориентированные простые цепи будем называть просто цепями.

Если в цепи дуга выходит из вершины и заходит в вершину , то она называется прямой дугой цепи. Если же дуга выходит из вершины и заходит в вершину , то она называется обратной дугой цепи.

Пусть - поток в сети и - цепь из в . Для каждой дуги цепи будем вычислять остаточную пропускную способность при данном потоке по следующему правилу: если дуга прямая, то , а если обратная, то . В свою очередь остаточную пропускную способность цепи при данном потоке будем определять по формуле .

Определение. Цепь из в называется дополняющей для , если .

Пример 2. В сети, изображенной на рис. 3.83, цепь, включающая последовательно вершины , является дополняющей для потока, рассмотренного в примере 1.

Одним из алгоритмов, позволяющих построить максимальный поток, является алгоритм Форда - Фалкерсона.

Алгоритм Форда - Фалкерсона. 0-й шаг. Пускаем по сети нулевой поток , т.е. полагаем для всех дуг .

-й шаг. Пусть к началу шага в сети течет поток . Для этого потока ищем дополняющую цепь из в .

Если такой цепи нет, то - искомый максимальный поток.

В противном случае, если для потока дополняющая цепь из в имеется, даем ей имя и определяем на множестве функцию по следующему правилу:

Построенная таким образом функция является потоком, и величина этого потока определяется равенством

.

Замечание. Возникает существенный вопрос: закончится ли работа алгоритма за конечное число шагов? Оказывается, хотя в подавляющем большинстве случаев алгоритм заканчивает свою работу за конечное число шагов, зацикливание возможно. Гарантировать построение максимального потока можно в том случае, если на каждом шаге производить увеличение потока вдоль кратчайших по числу дуг дополняющих цепей.

Доказательство алгоритма Форда - Фалкерсона приведено во второй части параграфа.

Пример 3. Построим максимальный поток для сети, изображенной на рис. 3.84,а.

◄ Шаг 0. Для любой дуги положим (на рисунке этот поток отмечать не будем, более того, договоримся и далее нулевой поток на дугах не отмечать), .

Шаг 1. - дополняющая цепь для потока (стрелки заменяют имена дуг, под каждой стрелкой записана остаточная пропускная способность соответствующей дуги ), , поток указан на рис. 3.84,б, .

Шаг 2. - дополняющая цепь для потока , , поток указан на рис. 3.84,в, .

Шаг 3. - дополняющая цепь для потока , , поток указан на рис. 3.84,г, .

Шаг 4. - дополняющая цепь для потока , , поток указан на рис. 3.84,д, .

Шаг 5. - дополняющая цепь для потока , , поток указан на рис. 3.84,е, .

а	б
в	г
д	е
Рис. 3.84.

Для потока нет ни одной дополняющей цепи из в . Следовательно, поток является максимальным. ►

Определение. Разрезом в сети называется пара множеств и , удовлетворяющих условиям:

1) , ;

2) ;

3) .

Через обозначим множество всех дуг, начала которых лежат в , а концы - в , а через - множество всех дуг, начала которых лежат в , а концы - в .

Определение. Положим . Число называется пропускной способностью разреза .

Определение. Разрез называется минимальным, если для любого разреза справедливо неравенство .

Во второй части параграфа будет доказано, что величина максимального потока в произвольной сети равна пропускной способности минимального разреза.

Если для сети найден максимальный поток, то минимальный разрез можно найти следующим образом: включить в множество вершину и все вершины , для каждой из которых существует цепь из в с остаточной пропускной способностью ; положить . Полученный таким образом разрез будет минимальным.

Пример 4. Вернемся к примеру 3. Используя найденный максимальный поток, несложно определить, что единственной вершиной, в которую можно добраться по цепи с положительной остаточной пропускной способностью, является вершина . Следовательно, пара множеств и образует минимальный разрез.