Лекция 12

§ 3.5. Обходы графов

Эйлеров цикл. Эйлеров граф. Эйлерова цепь. Гамильтонов цикл. Гамильтонов граф. Гамильтонова цепь.

Базовые понятия и утверждения

1. Эйлеров цикл и эйлерова цепь.В 1736 г. Леонард Эйлер опубликовал решение широко известной в то время задачи о кенигсбергских мостах. Задача эта состояла в следующем. На реке Прегель в Кенигсберге было два острова, соединенных между собой и с берегами семью мостами, как показано на рис. 3.62. Спрашивалось, можно ли, начиная с некоторого места суши, обойти все мосты по одному разу и вернуться назад?

Эмпирические попытки найти такой обход оканчиваются неудачей. Вклад Эйлера в решение задачи состоит в теоретическом обосновании невозможности такого обхода. Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой, а каждый мост - линией, соединяющей соответствующие точки. Получился рисунок, который мы называем диаграммой графа (рис. 3.63).

Рис. 3.62.	Рис. 3.63.

Используя современную терминологию, можно сказать, что Эйлер свел задачу об обходе мостов к поиску на данном графе цикла, содержащего все вершины и все ребра графа. Отправляясь от этого частного случая, Эйлер обобщил постановку задачи и доказал, что критерием существования такого рода цикла на произвольном связном графе является четность степеней всех его вершин.

Цикл на графе, содержащий все вершины и все ребра графа, стали называть эйлеровым циклом, а граф, на котором имеется эйлеровый цикл, -эйлеровым графом.

Цепь на графе (как замкнутая, так и незамкнутая), содержащая все вершины и все ребра графа, называют эйлеровой цепью(замкнутая эйлерова цепь есть не что иное, как эйлеров цикл).

Пример1. Граф на рис. 3.64 - эйлеров, поскольку содержит эйлеров цикл.

Пример2. Граф на рис. 3.65 содержит эйлерову цепь.

Пример3. Граф на рис. 3.66, очевидно не содержит ни одну эйлерову цепь и, в частности, не содержит ни одного эйлерова цикла.

Рис. 3.64.	Рис. 3.65.	Рис. 3.66.

Следующие два утверждения являются критериями существования эйлерова цикла и эйлеровой цепи на связном графе:

1) связный граф содержит эйлеров цикл тогда и только тогда, когда каждая его вершина имеет четную степень;

2) связный граф содержит эйлерову цепь тогда и только тогда, когда он имеет не более двух вершин нечетной степени.

Доказательство этих утверждений приведены во второй части параграфа.

Опишем алгоритм построения эйлерова циклана графе.

Пусть - связный граф, все вершины которого имеют четную степень.

1-й шаг.Произвольно выбираем некоторую вершинуи инцидентное ей ребро. Этому ребру присваиваем номер 1. Переходим по этому ребру в вершину, после чего ребро удаляем.

-й шаг.Пусть к началу этого шага мы находимся в вершине. Выбираем инцидентное этой вершине ребро, соблюдая следующие правила:

1) находясь в вершине , не следует выбирать ребро, соединяющеес, если имеется возможность иного выбора;

2) находясь в вершине , не следует выбирать ребро, которое является перешейком, т.е. таким ребром, при удалении которого граф, образованный оставшимися ребрами, распадается на ненулевые компоненты связности.

Выбранному ребру присваиваем номер , проходим по нему из вершиныв смежную с ней вершину, после чего ребро с номеромудаляем. Если после этого все ребра в графе оказались удаленными, то эйлеров цикл построен (порядок нумерации ребер соответствует последовательности их обхода в графе).

В противном случае удаляем ребро с номером , увеличиваемна единицу и повторяем-й шаг.

Пример 4.На рис. 3.67 изображен связный граф, степени всех вершин которого четны. Ниже приводится эйлеров цикл, построенный изложенным выше алгоритмом:

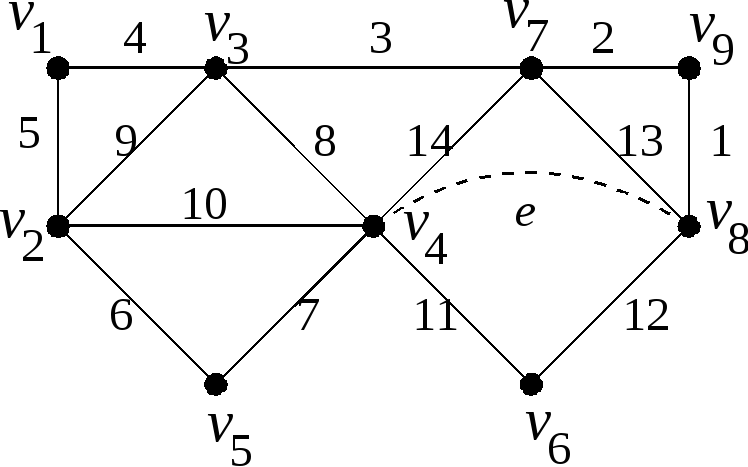
Пример 5.На рис. 3.68 изображен связный граф, у которого ровно две вершиныиимеют нечетную степень (ребрографу не принадлежит). Соединим вершиныи, имеющие нечетную степень, реброми построим на полученном графе эйлеров цикл, начав его с этого ребра:

.

Рис. 3.67.	Рис. 3.68.

Удалив из построенного эйлерова цикла первую вершину и ребро (), получим на исходном графе эйлерову цепь:

.

2. Гамильтонов цикл и гамильтонова цепь.Гамильтоновой цепьюграфа называется такая его простая цепь, которая проходит через каждую вершину ровно один раз. Замкнутая гамильтонова цепь называетсягамильтоновым циклом. Граф называетсягамильтоновым, если он обладает гамильтоновым циклом.

Гамильтонов цикл не обязан проходить по всем ребрам графа.

Простого и эффективного критерия существования гамильтонова цикла на графе не найдено. Однако известно несколько необходимых и достаточных условий существования гамильтоновых циклов [4].