
МП-2 / 6_3
.docxX0 = [ 2 1 6 11 4 8 7 2 3 0....
2 5 5 5 14 3 14 1 10 11....
5 1 6 3 13 2 14 0 5 12....
5 18 0 4 1 2 10 12 3 4....
2 2 2 1 1 12 4 0 3 3 ];
X = sort(X0);
n = length(X); %объем выборки
M = 7;
w = range(X);
b = w/M;
disp(sprintf('Размах w = %g', w))
disp(sprintf('Ширина интервала = %g', b))
[N, Z] = hist(X, M); %таблица частот N середины интервалов
disp('Середины интервалов группировки zi: ')
disp(Z)
disp('Частоты попадания выборочных значений N: ')
disp(N)
hold on
bar(Z, N/b, 1, 'g') %гистограмма частот
plot (Z, N/b, 'b', Z, N/b, 'bx') %полигон
hold off
NS = cumsum(N);
disp('Накопленные частоты:')
disp(NS)
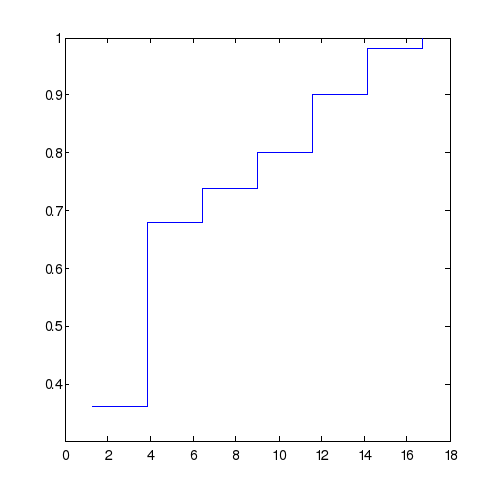
figure; stairs(Z, NS/n) %Эмпирическая функция распределения
x = sum(Z.*N)/n;
disp(sprintf('Выборочное среднее (оценка математического ожидания) ~x = %g', x))
Dx = (sum(Z.^2.*N) - n*x^2)/n;
disp(sprintf('Выборочная смещенная дисперсия ~Dx = %g', Dx))
disp(sprintf('Несмещенная дисперсия S^2 = %g', Dx*n/(n-1)))
disp(sprintf('Оценка выборочной медианы ~hx = %g', median(X)))
disp(sprintf('Оценка выборочной моды ~dx = %g', mode(X)))
alpha = 0.05;
disp('Доверительные интервалы для МО и дисперсии. Доверительная вероятность 0.95')
[m, sigma, m_int, sigma_int] = normfit(X, alpha);
disp(sprintf('%g < m = %g < %g', m_int(1), m, m_int(2)))
disp(sprintf('%g < sigma^2 = %g < %g', sigma_int(1)^2, sigma^2, sigma_int(2)^2))
disp('Проверить гипотезы H1: mx=Mo, Mo=x+0.1*s, H2: Dx=Ao, Ao=s^2*sqrt(2)')
Mo = x + 0.1*(Dx*n/(n-1))^0.5;
if Mo > m_int(1) && Mo < m_int(2)
disp(sprintf('%g < Mo = %g < %g. H1 верна.', m_int(1), Mo, m_int(2)))
else
disp(sprintf('Mo = %g. Не принадлежит (%g; %g). H1 не верна.', Mo, m_int(1), m_int(1)))
end
Ao = (Dx*n/(n-1))*(2^0.5);
if Ao > sigma_int(1)^2 && Ao < sigma_int(2)^2
disp(sprintf('%g < Ao = %g < %g. H1 верна.', sigma_int(1)^2, Ao, sigma_int(2)^2))
else
disp(sprintf('Ao = %g. Не принадлежит (%g; %g). H1 не верна.', Ao, sigma_int(1)^2, sigma_int(1)^2))
end
disp('Интервалы разбиения nn: ')
nn = [N(1) N(2) N(3)+N(4) N(5)+N(6)+N(7)];
disp(nn)
disp('Вероятность P попадания случайной величины в каждый из интервалов выбранного разбиения: ')
p(1) = normcdf(b, m, sigma);
p(2) = normcdf(2*b, m, sigma)-normcdf(b, m, sigma);
p(3) = normcdf(4*b, m, sigma)-normcdf(2*b, m, sigma);
p(4) = 1 - normcdf(4*b, m, sigma);
disp(p)
disp('Теоретические частоты ni = n*pi: ')
ni = n*p;
disp(ni)
disp('Данные для подсчета статистики Хи-квадрат:')
Hii = ((nn - ni).^2)./(ni);
disp(Hii)
Hib = sum(Hii);
hi = chi2inv(0.95,1);
if Hib > hi
disp(sprintf('Hib = %g1 > hi = %g2. Гипотеза о нормальном распределении не верна.', Hib, hi))
else disp(sprintf('Hib = %g1 <= hi = %g2. Гипотеза о нормальном распределении не верна.', Hib, hi))
end

 Размах
w = 18
Размах
w = 18
Ширина интервала = 2.57143
Середины интервалов группировки zi:
1.2857 3.8571 6.4286 9.0000 11.5714 14.1429 16.7143
Частоты попадания выборочных значений N:
18 16 3 3 5 4 1
Накопленные частоты:
18 34 37 40 45 49 50
Выборочное среднее (оценка математического ожидания) ~x = 5.24571
Выборочная смещенная дисперсия ~Dx = 20.1568
Несмещенная дисперсия S^2 = 20.5681
Оценка выборочной медианы ~hx = 4
Оценка выборочной моды ~dx = 2
Доверительные интервалы для МО и дисперсии. Доверительная вероятность 0.95
3.96312 < m = 5.28 < 6.59688
14.9821 < sigma^2 = 21.471 < 33.3412
Проверить гипотезы H1: mx=Mo, Mo=x+0.1*s, H2: Dx=Ao, Ao=s^2*sqrt(2)
3.96312 < Mo = 5.69924 < 6.59688. H1 верна.
14.9821 < Ao = 29.0877 < 33.3412. H1 верна.
Интервалы разбиения nn:
18 16 6 10
Вероятность P попадания случайной величины в каждый из интервалов выбранного разбиения:
0.2794 0.2088 0.3718 0.1400
Теоретические частоты ni = n*pi:
13.9714 10.4383 18.5899 7.0003
Данные для подсчета статистики Хи-квадрат:
1.1616 2.9634 8.5265 1.2854
Hib = 13.93681 > hi = 3.841462. Гипотеза о нормальном распределении не верна.
