53.Интервал мо норм. Гс

Генеральная совокупность 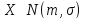, известна.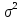

1)Задаем дов. вер-ть

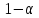
2)Задаем

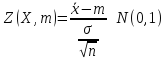
3)Поскольку N(0,1) симметрично, полагаем

Решаем неравенство относительно m:

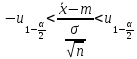
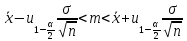
Это решение и определяет искомый интервал. Если бы была не известна, то можно было бы использоватьS

54.Интервал d и отн. D

Аналогично пред. вопросу.

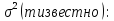
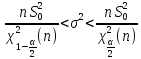
54. Проверка гипотез. Основное.

Относительно параметров выдвигаются гипотезы:

1)Проверяемая

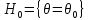
2)Альтернативные:

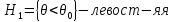
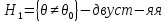
G – мн-во значений стат. Z. Зададим уровень знач-ти

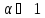
Разобьем 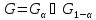– критическую и доверит-ую обл-ти из условия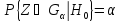или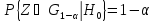. Выч-им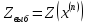по измерениям и воспользуемся правилом: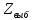

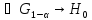принимается, иначе – отвергается в пользу 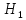на уровне значимости. Смысл состоит в том, что если верна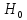, то событие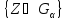практически невозможно(т.к.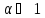), значит, если для данной выборки оно реализовалось, то следует считать, что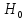не верна. Наоборот, еслисправедлива, топочти достоверно, поэтому, если оно произошло, то выборка не противоречит.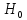

55.Ошибки. Выбор области.

Ошибка первого рода:отвергнуть

верную

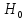
Ошибка второго рода: принять ложную

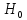
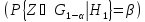
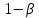-мощность крит-ия проверки

Если уменьшить 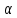, то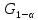расширится и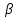возрастет.

Потому разумно выбирать 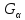из условия макс.при фикс.

Если – возр. по, то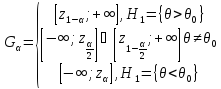

Где 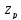-квантиль статистикиZ при условии .

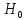56.Гипотеза о законе распр-ия

Алгоритм:

1)Выбрать уровень знач. 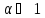, сформулировать

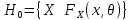
2)По выборке найти ММП оценки неизвестных параметров распределения

3)Разбить мн-во G значений Xна разряды

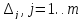
4)По предполагаемому 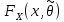найти вероятности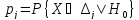. Напр. если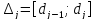, то

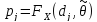-. По выборке посчитать частоты и вычислить значение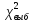статистики.

5) С помощью таблицы квантилей распределения хи-квадрат найти критическую область 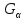или доверительную.

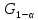6) Если , то принять, иначе – отвергнуть.