
- •1. Случ опыт. Пр-во эл. Исходов
- •2. Случ. События, оп-ии над ними
- •3. Классич. Опр-ие вероятности
- •4.Геометрическая вероятность
- •5.Статистическая вероятность
- •6.Аксиоматическая вероятность
- •7. Свойства вероятности
- •13. Одномерные случ. Величины.
- •14. Свдт.
- •15. Свнт.
- •16. Случайные векторы.
- •17. Зависимые и независимые св
- •37. Теорема Муавра-Лапласа
- •38. Мс. Основные понятия.
- •39. Эмпирич. Ф-ия распр-ия
- •40.Основные распределения.
- •53.Интервал мо норм. Гс
- •54.Интервал d и отн. D
- •54. Проверка гипотез. Основное.
- •55.Ошибки. Выбор области.
- •56.Гипотеза о законе распр-ия
37. Теорема Муавра-Лапласа
Пусть
 – число усп-ов вn
исп. Б. с вер-ю успеха
– число усп-ов вn
исп. Б. с вер-ю успеха
 и неудачи
и неудачи .
Тогда
.
Тогда
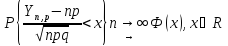
Справедливо
представление
 ,
где
,
где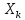 -
индикатор,
-
индикатор, .
Отсюда, применив ЦПТ, докажем требуемое.
.
Отсюда, применив ЦПТ, докажем требуемое.
Из
этой теоремы следует, что при
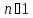 ,
приближенно справедливо
,
приближенно справедливо

Так же отсюда следует, что с ростом числа n биномиальное распределение приближается к нормальному, несмотря на то, что первое СВДТ, а второе – СВНТ
38. Мс. Основные понятия.
Предмет МС – изучение случ. яв-ий посредством обработки и анализа рез-ов наблюдений и измерений
СВ Х будем называть генеральной совокупностью(ГС) Х
Набор
 – случайная выборка объемаn
из ГС
– случайная выборка объемаn
из ГС
 -получен
в рез-те n-кр.
повт. одного и того же опыта, реализация
случ. выб-ки
-получен
в рез-те n-кр.
повт. одного и того же опыта, реализация
случ. выб-ки
В основе МС – выборочный метод, св-ва ГС устанавливаются на основе св-в случ. выб-ки
Первичная обработка:
1)Вариационный ряд
2)Статистический ряд
3)Интервальный статический ряд
39. Эмпирич. Ф-ия распр-ия
 -значения
статистич. ряда
-значения
статистич. ряда
 -количество
значений выборки, удовл.
-количество
значений выборки, удовл.

 –ЭмпФР
–ЭмпФР
Очевидно
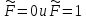 при
при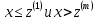 соотв-но.
соотв-но.
Гистограмма – график эмп. пл. р-ия

 –пром.
разб-я
–пром.
разб-я
Используют
также выборочную ф-ия распределения.
Все аналогично, вместо
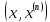 исп-т
исп-т
Очевидно, эмпир. ф-ия есть реализация ф-ии выборочной.
Сх.
Бер-ли. Успех
–
 ==true.
==true.
Тогда
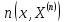 – ЧУ вn
исп-ях с
– ЧУ вn
исп-ях с
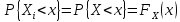
Исп-м ЗБЧ в форме Бернулли:
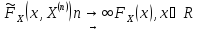
Для СВДТ отн. част. сх-ся к вер-м
Так же приближенно и для СВНТ
С
пом-ю т. Бернулли эмп-ая плот-ть распр-ия
дает прибл. пред-ие плот-ти вер-ти ГС:
 при большомn
и малом
при большомn
и малом
 .
.
40.Основные распределения.
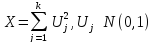 .
Тогда
.
Тогда
 ,
k
степеней свободы.
,
k
степеней свободы.
а) ,
,
б)Композиционнаяая
уст-ть:
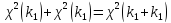
в) ,
,
г) ,
,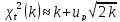
Распри-ие Стьюдента:
Пусть
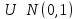 ,
,
а)

б)
в)р-ие.
симм-но,

Распр-ие Фишера:
Пусть
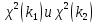 независимы. Тогда
независимы. Тогда
а)

б)Квантили:
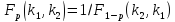
41.Распр-ие выб. дисперсии

Поскольку
 ,
то и
,
то и .
Поэтому
.
Поэтому .
Тогда
.
Тогда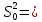
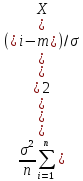
 .
Т.о.
.
Т.о.
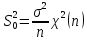 ,
или в станд. виде:
,
или в станд. виде: .
.
Распределение исправленной выборочной дисперсии:

Для исправ-ой дисперсии можно доказать:

42.Распр-ие выб-го среднего

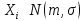 .
Потому,
в силу композиционной устойчивости
нормального закона, получаем:
.
Потому,
в силу композиционной устойчивости
нормального закона, получаем:
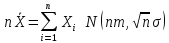
Далее,
поскольку линейное преобразование
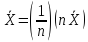 сохраняет нормальный закон распр-ия,
то
сохраняет нормальный закон распр-ия,
то .
Перейдя к стандартизированному виду,
получаем:
.
Перейдя к стандартизированному виду,
получаем:


Используем выб. аналог СКО:
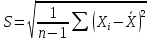
Тогда получается соотношение:

43.Распр-ие отношения D 2х ГС
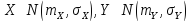 ,
m
изв-ны. Рассмотрим з распр-ия стат-ки:
,
m
изв-ны. Рассмотрим з распр-ия стат-ки:
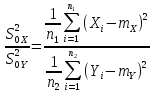
Можно записать:
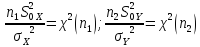

Откуда:

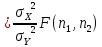
Мат. ожидания неизвестны. Отношение испр-ых выб. дисперсий:

Имеют место аналогичные соотношения:

44.Точечные оценки параметров
Точечная
оценка параметра
 называется статистика
называется статистика ,
реализации которой исп-ся как прибл.
значения параметра
,
реализации которой исп-ся как прибл.
значения параметра
Качество характеризуется:
1)Несмещенность:

Ассимптотическая несмещенность:

Показывает точность «в среднем»
2)Состоятельность:
Если с ростом n она сходится по вер-ти к этому параметру:
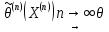
3)Эффективность:
Если
 ,
при том несмещенная, что для
,
при том несмещенная, что для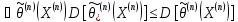 ,
то
,
то – эффективная.
– эффективная.
45.Несм-ть выб. дисп и среднего.
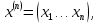
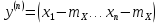
Т.к. выборочные D X и Y равны, то
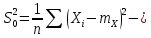
 .
Получим:
.
Получим:

 -Смещ-ая
-Смещ-ая
Однако, обладает асимпт-ой несм.
Несм-ть среднего:


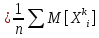
Поскольку
 распр так же, как ГС,
распр так же, как ГС,

 ,
что означает несмещнность среднего
как оценки этого момента.
,
что означает несмещнность среднего
как оценки этого момента.
46.Несм-ть выб. дисп.
Исправленная выборочная дисперсия при неизвестном m:

Рассуждая аналогично, как и для для не исправленной, получаем несмещенную оценку:

Т.о.
исправленная выборочная дисперсия
является несмещенной оценкой

47.Состоятельность
Начальные и центральные моменты 1-го и 2-го порядка являются состоятельными оценками ГС.
Док-во для выборочного среднего:
 -состоятельная
оценка МО для ГС Х с конечной дисперсией.
-состоятельная
оценка МО для ГС Х с конечной дисперсией.
Условие состоятельности
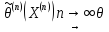
непосредственно следует из закона больших чисел.
Состоятельность этой оценки, в конечном счете, обеспечивается тем, что
 .
.
Так же несложно доказать, что если статистика является асимптотически несмещенной и ее дисперсия схходится к нулю, то она состоятельна.
48.Эфф-ть выб-го среднего.
Пусть
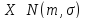 .
Исследуем эффективность
.
Исследуем эффективность для оценкиm
для оценкиm
 .
Найдем
правую часть неравенства Крамера-Рао:
.
Найдем
правую часть неравенства Крамера-Рао:
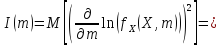
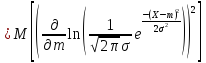
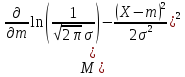

Правая часть неравенства равна:
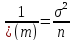 ,
т.е. совпадает с левой частью. Таким
образом выборочное среднее эффективно
оценивает маетматическое ожидание
нормальной генеральной совокупности
Х.
,
т.е. совпадает с левой частью. Таким
образом выборочное среднее эффективно
оценивает маетматическое ожидание
нормальной генеральной совокупности
Х.
49.Метод макс. правдоподобия
Пусть
закон распр-ия генеральной совокупности
описывается
 ,
или
,
или где
где – вектор неизвестных параметров.
– вектор неизвестных параметров.
Функция правдоподобия(ФП):
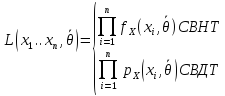
Требуется
найти
 ,
доставляющий максимум ФП при фикс.
,
доставляющий максимум ФП при фикс.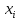 .
Можно исп-ть логарифм ФП. Уравнения
правдоподобия(c
ln):
.
Можно исп-ть логарифм ФП. Уравнения
правдоподобия(c
ln):

Пример:
 .
ММП оц.
.
ММП оц. = ?
= ?
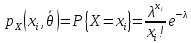




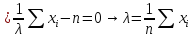
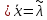 .
<Вывод>
.
<Вывод>
51.Метод моментов
Пусть
закон распр-ия генеральной совокупности
описывается
 ,
или
,
или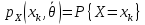 где
где – вектор неизвестных параметров.
– вектор неизвестных параметров.
Определим r моментов(СВНТ):

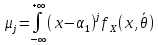
Аналогично
для
 .
Приравнявr
найденных теор. мом-ов к вы-ым получим
систему для
.
Приравнявr
найденных теор. мом-ов к вы-ым получим
систему для
 :
:
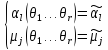
Пример.



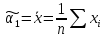
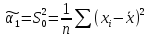
Получаем:
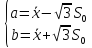 .
Т.е. ММ-оценки:
.
Т.е. ММ-оценки:
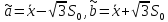
 -выборочное
СКО
-выборочное
СКО
52.Интервальные оценки.
Доверительным
интервалом называется интервал
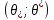 ,
накрывающий истинное значение
,
накрывающий истинное значение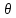 с заданной вероятностью
с заданной вероятностью ,
кот. называется доверительной вер-ю,
где
,
кот. называется доверительной вер-ю,
где -уровень
значимости.
-уровень
значимости.
Практический
смысл имеет
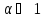
Алгоритм:
1)Задать
 или
или
2)Выбрать
статистику
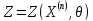 с
изв-ым зак-ом расп-ия
с
изв-ым зак-ом расп-ия
3)По
этому закону найти
 :
:
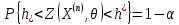
4)Решить неравенства
 (5.13)
(5.13)
относительно
 :
: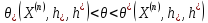 ,
что экв-но 5.13, т.е. вып-ся с вероят-ю
,
что экв-но 5.13, т.е. вып-ся с вероят-ю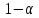
Отсюда по выборке найдем доверительный интервал:

Определение
 неоднозначно, потому обычно полагают
неоднозначно, потому обычно полагают
 , где
, где
 –p-квантиль
рас-ия стати. Z,
поскольку для симм-ых рас-ий(St(k),
N(0,1))
интервал будет наименьшим, а для
несим-ых(
–p-квантиль
рас-ия стати. Z,
поскольку для симм-ых рас-ий(St(k),
N(0,1))
интервал будет наименьшим, а для
несим-ых( )
– бликим к минимальному.
)
– бликим к минимальному.
