7. Свойства вероятности
1.
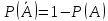
2.
3.
Если A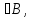
то
P(B)
4.
5.P(A+B)=P(A)+P(B)-P(AB)
Докажем (3):
Пусть
A
.
Тогда B=A+(B-A).
Поскольку A
и (B-A)
несовместны, из аксиомы сложения
получаем: P(B)=P(A)+P(B-A).
Поскольку P(B-A)
,
наше неравенство выполняется
Докажем (5):
A+B=A+(B-A) и B=(B-A)+AB. Слагаемые в правых частях несовместны, потому из аксиомы сложения получаем: P(A+B)=P(A)+P(B-A), P(B)=P(B-A)+P(AB). Исключив отсюда P(B-A), получим формулу.
8. Условная вероятность
Пусть
(
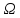,F,
P)
– вероятностное пространство, A,B
,P(B)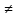
0.
Тогда условной вероятностью события
А при условииB
называется число
Условная вероятность обладает всеми свойствами безусловной, т.к. для нее выполняются аксиомы.
Из определения безуслвоной вероятности следует теорема умножения: P(AB)=P(A|B)P(B)= P(A)P(B|A), которая обобщается на случай n событий:
9. Независимость событий.
Говорят, что событие А не зависит от события В, если P(A|B)=P(A)
Независимость событий взаимна.
Докажем:
Пусть P(A|B)=P(A). С учетом теоремы умножения получаем: P(B)P(B|A)=P(A)P(B)=P(AB)=P(A)P(B|A), откуда, после сокращения на P(A), имеем: P(B)=P(B|A)
Т.е. если P(AB)=P(A)P(B), то А и В независимы и наоборот.
Независимость
n>2
событий называется независимостью в
совокупности, т.е.
– незав. в совок-ти, если для
– набора событий выполняется равенство
10.Формула полной вероятности
Во
многих случаях событие А может произойти
только вместе с одним из событий
.
Множество {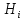
}
обладает св-ами:
а)в
каждом опыте обязательно происходит
некот.
,
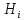т.е.
б)События
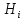попарно несовместны.
Тогда
говорят, что
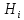– гипотезы, а их объед. – полная группа
событий
Формула полной вероятности:
Пусть
А может произойти только с некоторым
,
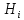образующ. полную группу. Тогда:
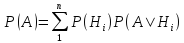
Док-во:
Посльку
попарно несовместны, то, с учетом аксиомы
сложения имеем:
=
P(
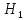)P(A|
)…
11.Формула Байеса
В условиях теоремы о полной вер-ти:
Эта формула напрямую следует из теоремы умножения и формулы полной вероятности.
12. Схема Бернулли. Формула.
Повторные испытания – посл. пров-ие n раз одного опыта.
Сх. Бернулли – n повт. испыт, т.ч.:
1)сущ-т
2 исхода: А(успех) и
2)испытания независимы
3)P(A)
= p
= const,
P(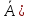
=1-p=q
Формула Бернулли. Вер-ть того, что в n испытаниях по сх. Б произойдет ровно m успехов равна
Док-во:
Событие
={ровноm
успехов в n
испытаниях} состоит из эл. исходов
(посл-ей A
и
),
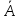сод-ихm
событий А и n-m
событий
.
Вер-ть любого из таких исходов, в силу
независимости испытаний равна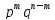
.
Число этих исходов равно числу способов
выбораm
мест для событий А из n
мест в последовательности событий А и
,
т.е. равно
.
Отсюда и следует формула Бернулли.
13. Одномерные случ. Величины.
Пусть
(
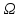,F,
P)
– вер-ое пр-во. Числовая ф-ия X=X(
)
с обл. опр-ия
– СВ, если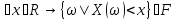
,
т.е. сущ. хотя бы простейшее соотн. с
вероятностью.
–функция
распределения(вероятностей) СВ X.
В силу определения СВ X
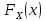определена на всей числ. прямой.
Формулы:
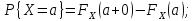
Док-во первой формулы:
Рассм.
3 события:
,
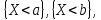
где
a<b.
Очевидно,
Причем
события в правой части несовместны.
Поэтому, исп. аксиому сложения:
или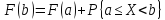
,
откуда следует формула.
Св-ва ф-ии распределения:
1)
2)
не убывает
3)
непр. слева в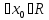
4)
;