
- •1. Случ опыт. Пр-во эл. Исходов
- •2. Случ. События, оп-ии над ними
- •3. Классич. Опр-ие вероятности
- •4.Геометрическая вероятность
- •5.Статистическая вероятность
- •6.Аксиоматическая вероятность
- •7. Свойства вероятности
- •13. Одномерные случ. Величины.
- •14. Свдт.
- •15. Свнт.
- •16. Случайные векторы.
- •17. Зависимые и независимые св
- •37. Теорема Муавра-Лапласа
- •38. Мс. Основные понятия.
- •39. Эмпирич. Ф-ия распр-ия
- •40.Основные распределения.
- •53.Интервал мо норм. Гс
- •54.Интервал d и отн. D
- •54. Проверка гипотез. Основное.
- •55.Ошибки. Выбор области.
- •56.Гипотеза о законе распр-ия
1. Случ опыт. Пр-во эл. Исходов
Случайный опыт – мат. модель, состоящая в осущ-ии некот. комплекса условий и набл-ии рез-та, кот. интерпретируется, как случайный исход(случайное событие). Случайное событие в результате опыта может как произойти, так и нет.
Каждому
опыту ставится в соответствие пространство
элементарных исходов
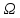 .
Это множ-во простейших взаимоисключающих
исходов {
.
Это множ-во простейших взаимоисключающих
исходов {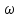 }
таких, что результатом опыта является
только один исход
}
таких, что результатом опыта является
только один исход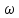
Пример. Опыт состоит в бросании одной правильной шестигранной кости и наблюдении числа выпавших очков.
Пространство
элементарных исходов
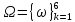 состоит
из 6 элементов.
состоит
из 6 элементов.
2. Случ. События, оп-ии над ними
Случайное
событие – любое подмножество пространства
элементарных исходов
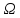 .Cобытие
А наступило, если результатом случайного
опыта явился любой из элементарных
исходов
.Cобытие
А наступило, если результатом случайного
опыта явился любой из элементарных
исходов
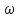 ,
входящих в подмножество А.
,
входящих в подмножество А.
Основные понятия:
1)Событие
А =
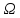 – достоверное
– достоверное
2)А
=
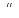 - невозможное
- невозможное
3)А
влечет за собой B(А B),
если любой элем. исход в А, принадл. В
B),
если любой элем. исход в А, принадл. В
4)A+B – состоит из тех элем. исходов, кот. входят в А или В
5)AB – и в А, и в В.
6)А-В
- есть в А, нет в В. А-В=А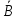
7)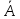 – противоп-ое;А не произошло
– противоп-ое;А не произошло
8)А
и В несовместны, если AB=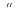
Св-ва:
1)Комм-ть: A+B=B+A; AB=BA
2)Асс-ть: A+(B+C)=(A+B)+C; A(BC)=(AB)C
3)Дистр-ть: (A+B)C=AC+BC; AB+C=(A+C)(B+C);
4)Погл-ие:A+A=A;
AA=A; A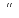 =
=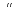 ;
A+
;
A+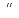 =A;
A
=A;
A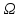 =A; A+
=A; A+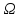 =
=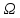
5)Правила де Моргана
3. Классич. Опр-ие вероятности
Классическая
схема
– случ опыт,
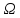 кот. конечно и все
кот. конечно и все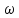 равновозможны.
равновозможны.
Пусть случайный опыт есть классическая схема. Тогда веротность события А:
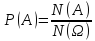
Свойства:
1)P(A)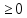 для любого А
для любого А
2)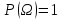
3)P(A+B)=P(A)+P(B),
если
AB=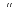
А
также
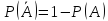 ,
,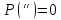 и др.
и др.
4.Геометрическая вероятность
Геометрическая схема:
1)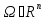 измеримо и имеет конечную меру
измеримо и имеет конечную меру
2)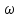 (точка)
выбирается так, что вероятность попадания
в область А определяется лишь величинойmes(A)
и пропорциональна ей.
(точка)
выбирается так, что вероятность попадания
в область А определяется лишь величинойmes(A)
и пропорциональна ей.
Тогда вероятность:
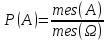
Те же свойства, что и у класс. вер-ти:
1)P(A)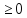 для любого А
для любого А
2)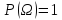
3)P(A+B)=P(A)+P(B),
если
AB=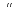
А
также
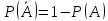 ,
,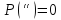 и др.
и др.
5.Статистическая вероятность
Для
широкого круга случайных явлений
характерна устойчивость относительных
частот. При достаточно большом n
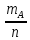 сохр. почти пост. значение, т.е.
сохр. почти пост. значение, т.е.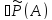 ,
около которой колеблется
,
около которой колеблется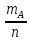 .
.
Таким образом, соб. А обладает вероятностью, если:
а)можно провести в неизменных условиях любое число независимых испытаний, в каждом из которых может появиться А
б)Частота А для больших серий колеблется около неизвестной постоянной. За ее значение можно приближенно взять частоту А при большом кол-ве испытаний.
Статистическая вероятность обладает такими же свойствами, как и классическая.
Впрочем, данное описание вероятностни носит описательный, а не строго-математический характер.
6.Аксиоматическая вероятность
Пусть
каждому случайному событию А поставлено
в соот-ие P(A),
т.е. на множестве F
событий опыта задана ф-ия P(A).
События A+B,
AB,
A-B,
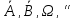 также принадлежатF.
Множ-во F
– алгебра событий. Если пр-во элементарных
исходов конечно, то алгеброй событий
будет множество всех его подмножеств,
включая пустое множество.
также принадлежатF.
Множ-во F
– алгебра событий. Если пр-во элементарных
исходов конечно, то алгеброй событий
будет множество всех его подмножеств,
включая пустое множество.
Пусть
F
– алгебра событий, образ. на пр-ве
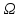 .
Предположим, что каждому элементу(событию)
.
Предположим, что каждому элементу(событию)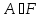 поставлено в соот-ие числоP(A).
Эта функция назыв. вер-ю, если:
поставлено в соот-ие числоP(A).
Эта функция назыв. вер-ю, если:
1)P(A)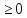 (акс. неотрицательности)
(акс. неотрицательности)
2)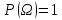 (нормированности)
(нормированности)
3)P(A+B)=P(A)+P(B),
если AB=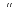 (аксиома сложения)
(аксиома сложения)
Тройка
(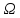 ,F,
P)
– вероятностное пространство.
,F,
P)
– вероятностное пространство.
