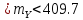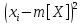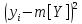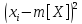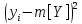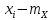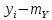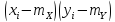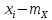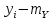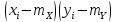Определение математического ожидания и дисперсии.
Математическое ожидание определяется по формуле:
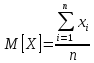
Что, по сути, является просто средним арифметическим. Итак:
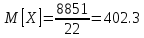
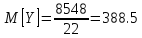
Для дисперсии используется формула:
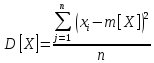
Выведем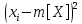
|
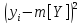
время |
12:00 |
13:00 |
13:15 |
13:25 |
13:46 |
13:55 |
14:00 |
14:13 |
14:39 |
14:43 |
15:00 |
|
|
767,29 |
470,89 |
161,29 |
94,09 |
1,69 |
0,49 |
1,69 |
18,49 |
53,29 |
53,29 |
127,69 |
|
|
3080,25 |
1892,25 |
1806,25 |
156,25 |
3540,25 |
420,25 |
992,25 |
552,25 |
1406,25 |
2862,25 |
812,25 |
|
время |
15:30 |
15:34 |
15:56 |
16:00 |
16:04 |
16:14 |
16:26 |
16:39 |
17:00 |
17:30 |
18:00 |
|
|
28,09 |
5,29 |
18,49 |
0,49 |
1,69 |
28,09 |
2,89 |
2,89 |
1,69 |
151,29 |
204,49 |
|
|
4422,25 |
3906,25 |
5402,25 |
4290,25 |
1892,25 |
5852,25 |
4830,25 |
132,25 |
42,25 |
2,25 |
132,25 |
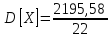=99.8
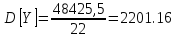
Определение среднеквадратичного отклонения.
Среднеквадратичное отклонение считается по формулам:
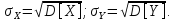
Получаем:
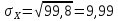
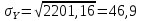
Определение ковариации.
Ковариация находится по формуле:
|
|
|
|
|
|
|
|
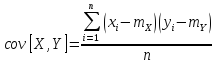
27,7 |
55,5 |
1537,35 |
-5,3 |
-66,5 |
352,45 |
|
21,7 |
43,5 |
943,95 |
-2,3 |
62,5 |
-143,75 |
|
12,7 |
42,5 |
539,75 |
-4,3 |
-73,5 |
316,05 |
|
9,7 |
-12,5 |
-121,25 |
0,7 |
-65,5 |
-45,85 |
|
-1,3 |
59,5 |
-77,35 |
-1,3 |
-43,5 |
56,55 |
|
0,7 |
-20,5 |
-14,35 |
-5,3 |
-76,5 |
405,45 |
|
-1,3 |
31,5 |
-40,95 |
1,7 |
69,5 |
118,15 |
|
-4,3 |
-23,5 |
101,05 |
1,7 |
11,5 |
19,55 |
|
-7,3 |
-37,5 |
273,75 |
-1,3 |
6,5 |
-8,45 |
|
-7,3 |
53,5 |
-390,55 |
-12,3 |
1,5 |
-18,45 |
|
-11,3 |
-28,5 |
322,05 |
-14,3 |
11,5 |
-164,45 |
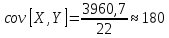
Подсчёт коэффициента корреляции.
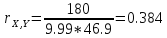
Искомая корреляция оказалась равной 0,384. Она относится к слабой корреляции прямого типа.
3. Расчёт доверительных интервалов. Доверительный интервал для математического ожидания.
Найдем доверительный интервал для математического ожидания при условии, что дисперсия генеральной величины неизвестна, а доверительная вероятность равна 1 – α.
Для расчета доверительного интервала применим формулы:
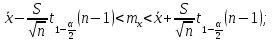
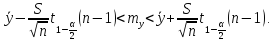
где
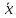– среднее значение величины X;
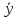– среднее значение величины Y;
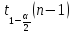– квантиль распределения Стьюдента с
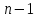степенью свободы;
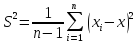– несмещенное выборочное стандартное
отклонение;
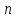– объем выборки(кол-во строк в табл.).
Для начала
определим квантиль распределения
Стьюдента, ориентируясь на сводную
таблицу из учебника, взяв
:
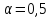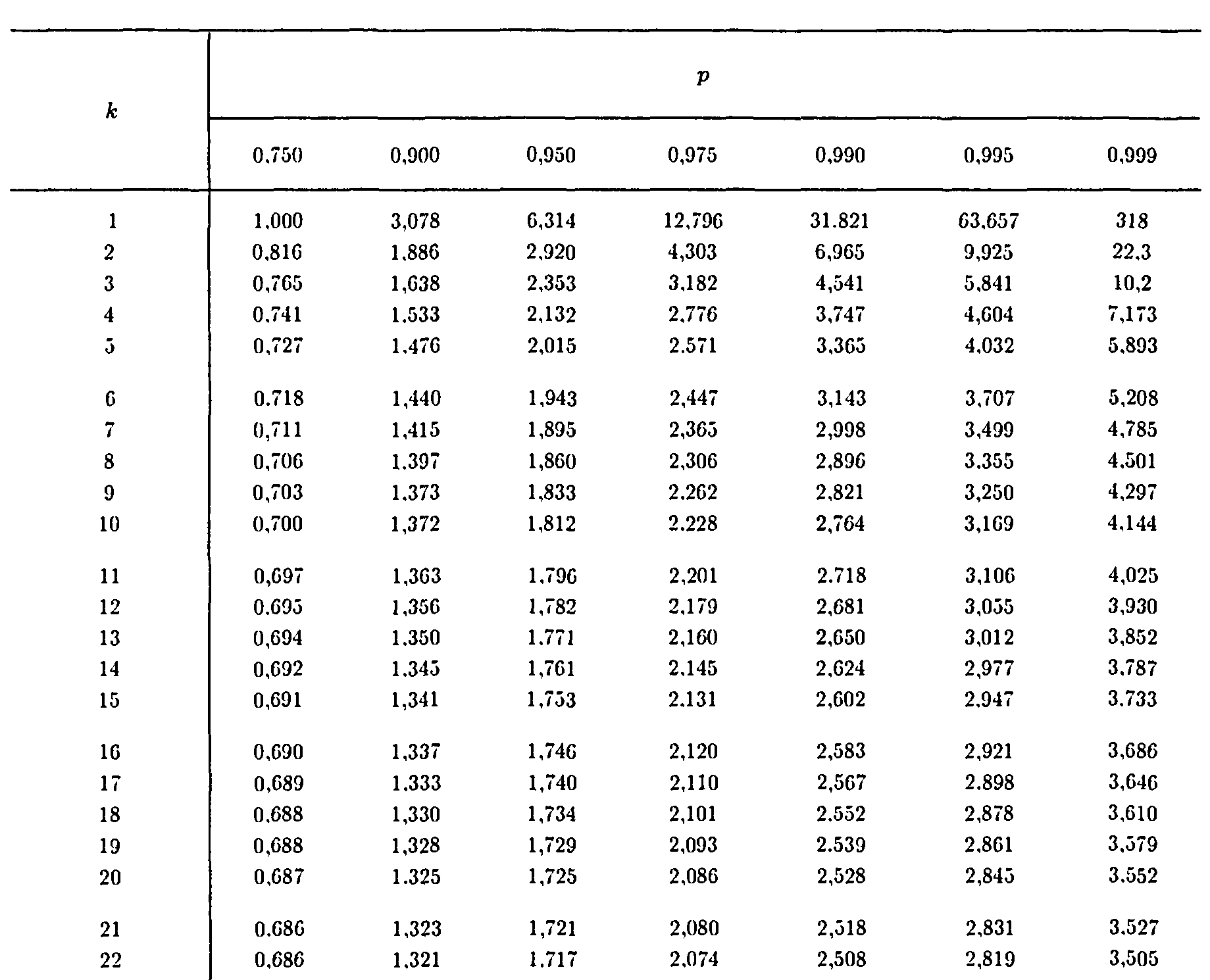
Мы имеем p=0.975 а, k=n-1=22-1=21. По этим данным выбираем из таблицы квантиль распределения Стьюдента, и он оказывается равен t=2.08. Теперь посчитаем S:
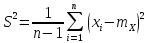
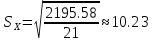
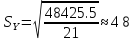
Подставим полученные значения в неравенство для доверительного интервала:
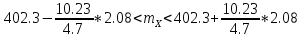
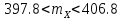
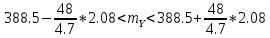
367.23