МП-2 / Prishutova_E_A mp_24_l_1
.docxЛабораторная работа №1
Вариант 21
function [ ] = terver( )
X0 = [ 2 3 6 0 4 4 1 4 2 4 7 4 6 5 2 5 3 2 0 2 5 2 0 4 4 0 4 5 3 2 2 3 3 2 3 4 4 2 3 4 3 2 2 0 6 3 3 4 2 5 ];
disp('Вариационный ряд: ')
X = sort(X0)
n = length(X); %объем выборки
M = 7;
w = range(X); %размах
b = w/M;
c=0;
s=0;
disp('Статистический ряд:')
while c~=8
for j=1:50
if (X(j)==c)
s=s+1;
end
end
disp(sprintf('%g %g', c,s))
c=c+1;
s=0;
end
disp(sprintf('Размах w = %g', w))
disp(sprintf('Ширина интервала = %g', b))
[N, Z] = hist(X, M);
%таблица частот N середины интервалов
disp('Середины интервалов группировки zi: ')
disp(Z)
disp('Частоты попадания выборочных значений N: ')
disp(N)
hold on
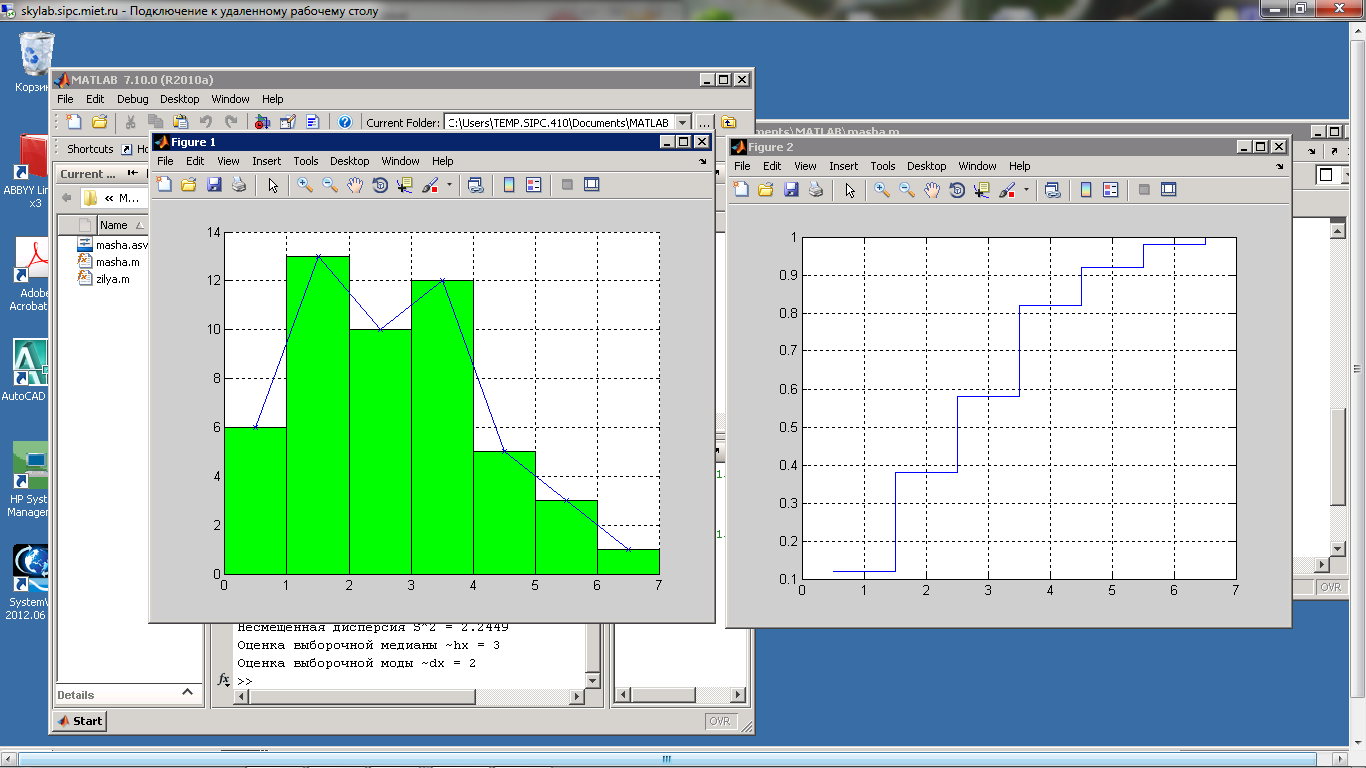
bar(Z, N/b, 1, 'g') %гистограмма частот
plot (Z, N/b, 'b', Z, N/b, 'bx') %полигон
grid on
hold off
NS = cumsum(N);
disp('Накопленные частоты:')
disp(NS)
figure; stairs(Z, NS/n) %Эмпирическая функция распределения
grid on
x = sum(Z.*N)/n;
disp(sprintf('Выборочное среднее (оценка математического ожидания) ~x = %g', x))
Dx = (sum(Z.^2.*N) - n*x^2)/n;
disp(sprintf('Выборочная смещенная дисперсия ~Dx = %g', Dx))
disp(sprintf('Несмещенная дисперсия S^2 = %g', Dx*n/(n-1)))
disp(sprintf('Оценка выборочной медианы ~hx = %g', median(X)))
disp(sprintf('Оценка выборочной моды ~dx = %g', mode(X)))
end
>> terver()
Вариационный ряд:
X =
Columns 1 through 7
0 0 0 0 0 1 2
Columns 8 through 14
2 2 2 2 2 2 2
Columns 15 through 21
2 2 2 2 2 3 3
Columns 22 through 28
3 3 3 3 3 3 3
Columns 29 through 35
3 4 4 4 4 4 4
Columns 36 through 42
4 4 4 4 4 4 5
Columns 43 through 49
5 5 5 5 6 6 6
Column 50
7
Статистический ряд:
0 5
1 1
2 13
3 10
4 12
5 5
6 3
7 1
Размах w = 7
Ширина интервала = 1
Середины интервалов группировки zi:
Columns 1 through 4
0.5000 1.5000 2.5000 3.5000
Columns 5 through 7
4.5000 5.5000 6.5000
Частоты попадания выборочных значений N:
6 13 10 12 5 3 1
Накопленные частоты:
6 19 29 41 46 49 50
Выборочное среднее (оценка математического ожидания) ~x = 2.7
Выборочная смещенная дисперсия ~Dx = 2.2
Несмещенная дисперсия S^2 = 2.2449
Оценка выборочной медианы ~hx = 3
Оценка выборочной моды ~dx = 2
>>