
тема 3
.docx
Сбор, регистрация и упорядочение данных в ходе любого исследования завершается формированием статистической совокупности.
Статистическая совокупность – совокупность объектов или явлений одного вида, объединенных по определенному признаку.
Для всех явлений, которые изучаются в медицине, характерна изменчивость, вариабельность.
Прежде чем|перед тем как| давать характеристику вариабельности| совокупности|, имеющей разные|различные| значения признаков|, необходимо иметь единую|единую| типичную|типовую| для совокупности величину| (показатель), что позволяет дать ее обобщённую характеристику. Для этого применяются средние величины, которые|какие| рассчитываются только по количественным признакам|, то есть определение средней для атрибутивных признаков невозможно.
Средние величины дают обобщенную количественную характеристику определенного признака в статистической совокупности при определенных условиях места и времени.
Применение средних величин в практике здравоохранения:|здравоохранительный|
• для характеристики организации работы учреждений (средняя занятость койки, средний срок пребывания в стационаре и др.);
-
для характеристики показателей физического развития (длина, масса тела, окружность головы новорожденных|, но|да| др.);
-
для анализа клинико-физиологических показателей (частота| пульса, дыхания, уровень артериального давления и | др.);
• для оценивания данных медико-социальных и санитарно-гигиенических исследований (среднее число лабораторных исследований, средние нормы питательного рациона, средний уровень радиационного загрязнения и|да| др.).
Обязательным условием расчета средних величин для исследуемой совокупности является ее однородность.
Варианты решения проблемы неоднородности:
-- исключение отдельных вариант из последующего анализа (с использованием соответствующих методик оценки),
-- проведение расчета погрупповых средних с определением максимальных и минимальных колебаний.
Свойством средней величины является ее обобщающая характеристика. Средняя величина рассчитывается путем сопоставления абсолютных или относительных величин.
Основные требования для расчета средних величин:
-
качественно однородная совокупность
-
достаточное число наблюдений.
Необходимое число наблюдений рассчитывается по соответствующим методикам в зависимости от характера данных и дизайна исследования. Распространенный шаблонный подход отбора не меньше N (30, 50, 100) пациентов является априорным, что недопустимо в клинических исследованиях.
Средняя величина имеет двойственный характер:
-- с одной стороны характеризует совокупность в целом,
-- с другой |— является основой|основанием| для оценки отдельных единиц
совокупности|, их разнообразия и изменчивости|переменчивости|.
1. По форме расчета выделяют:
а) среднюю арифметическую величину;
б) среднюю гармоничную величину;
в) среднюю геометрическую величину;
г) среднюю квадратичную, кубическую, и другие величины.
2. По охватыванию|охватом| совокупности выделяют:
а) групповую среднюю величину;
б) общую среднюю величину.
Средняя арифметическая является самым распространенным видом средних величин. Обозначается как X,однако, часто средняя арифметическая отражается|обозначается| буквой М (лат. Media|). По характеру данных она может быть простой или взвешенной|.
Средняя арифметическая простая определяется как сумма вариант вариационного ряда, разделенная на их число.
Отдельные элементы (значения) совокупности однородных по качественному составу предметов, явлений, параметров являются вариантами. Всю их совокупность можно представить в виде вариационного ряда, который является основой для определения средних величин.
Вариационный ряд – это ряд вариант и соответствующих им частот.
Вариационный ряд — совокупность числовых значений признака (вариант), которые могут быть не систематизированы по своему абсолютному значению (неранговый ряд) или систематизированы в порядке роста или уменьшения (ранговый ряд).
Вариационный ряд может быть:
-
Простым (каждая варианта представлена отдельно, частота каждой из них равняется единице).
-
Если варианты сгруппировать по их абсолютным значениям|, то можно получить сгруппированный вариационный ряд, где каждая варианта имеет свою частоту.
-
Вариационные ряды, где значение вариант представлено в виде интервалов, называются интервальными.
-
Сгруппированный интервальный вариационный ряд можно получить путем объединения вариант в группы. При этом надо помнить, что:
а) размер вариационных групп должен зависеть от природы| явления;
б|б|) имеет смысл определять одинаковые интервалы;
в) границы вариационных групп не должны повторяться.
Все вариационные ряды по качественной характеристике распределяются на:
-
Дискретные (|варианты представлены только целыми числами или получены в результате подсчетов|вычисления|);
-
Инкретные (непрерывные|), где варианты представлены как целыми, так и дробными числами, или являются результатом измерений. |н
Клинические параметры являются в основном примером|прикладом| инкретных| вариант.
В ходе исследования вопрос о числе| вариационных групп решают с учетом|разреша характера материала| и численностьи совокупности. Характерные особенности распределения|делению| не выявляются|проявляются|, если при незначительном числе единиц наблюдения взять значительное число групп или если число групп является недостаточным.
Одним из вариантов автоматического группирования|группировки| есть использование|употребление| формулы Стерджеса (для определения оптимального числа групп):
n=1+3,322 х lgN n – число групп; N – число единиц наблюдения
Использование|употребление| данной формулы целесообразно при большом|великом| числе единиц наблюдения.
Другим вариантом является метод определения амплитуды ряда (разница между максимальным и минимальным значением варианта). Для решения вопроса о числе групп необходимо подать статистическую совокупность в виде рангового ряда ( разместить ее единицы в определенном порядке). При численности совокупности менее 100 единиц не целесообразно планировать больше 10 групп.
Этапы составления|сдает| интервального вариационного ряда:
-
определение амплитуды ряда;
-
определение числа групп;
-
определение величины интервала.
Расчет средних величин базируется на значениях вариант.
Если варианта представлена в виде интервала, то за величину ее в каждом из них принимают центральную варианту ( середину|средину| интервала).
Для дискретного ряда| центральная варианта определяется как полусумма| одного интервала.
Для инкретного ряда ею является полусумма начальных|первоначальных| значений двух соседних интервалов.
Свойства средней арифметической величины:
1) произведение средней на сумму частот равняется сумме произведений каждой варианты на соответствующие им частоты;
2) сумма отклонений отдельных вариант от средней арифметической равняется нулю;
3) если все варианты совокупности увеличить или уменьшить на постоянную величину, то средняя арифметическая соответственно изменится на такую же величину;
4) если все варианты совокупности увеличить или уменьшить в определенное количество раз (А), то средняя арифметическая соответственно изменится в такое же количество раз (А);
5) если все частоты (значения) разделить или умножить на какое-то число, то средняя арифметическая вследствие этого не изменится — если мы увеличиваем или уменьшаем равнозначно частоты всех вариант, мы не изменяем вес каждой отдельной варианты ряда.|.
Взвешенная средняя арифметическая определяется как сумма произведений вариант на соответствующие частоты, разделенная на общее число наблюдений. Частоты отражаются|обозначаются| буквою| f |и указывают, сколько раз встречается каждая варианта в вариационном ряду.
Если варианты обозначить X, частоты f, общее число наблюдений, — буквой N, арифметическую сумму символом Σ, то формула средней арифметической будет иметь вид:
1) для простого ряда (простая средняя арифметическая):
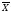
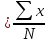
2)для сгруппированного ряда (взвешенная средняя арифметическая):
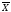 =
=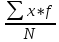
Средняя гармоническая определяется в случаях, когда известны данные числителя при отсутствии данных о знаменателе.
Xгарм=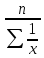
Средняя геометрическая определяется для параметров, изменения значений которых происходят в геометрической прогрессии (изменение численности населения в период между переписями, прирост массы тела новорожденных в течение отдельных месяцев жизни и др.).
Формула для расчета простой средней геометрической:
Mгеом=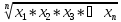
или
lgMгеом=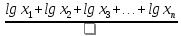
Логарифм средней геометрической равняется сумме логарифмов всех членов ряда, разделенных на их число. Логарифм полученного результата есть средняя геометрическая.
Иногда в здравоохранении|здравоохранительный| для характеристики показателей используют среднюю прогрессивную|. Данная величина| рассчитывается из|с| вариант, которые|какие| имеют качественно более высокий уровень относительно среднего значения. Такая средняя может служить базой для определения оптимального уровня определенного показателя|.
С|дредние величины, имеющие относительный характер:
Медиана (Me|) — срединная, центральная варианта, который делит вариационный ряд на две равных части. В ряду с парным|четным| числом наблюдений центральное положение имеют две величины. Если числовые значения этих двух величин разные|различные|, то за медиану берется их полусумма|.
Квартили — значения, которые делят две половины совокупности (разделенные медианой) еще раз пополам (от слова кварта — четверть). Выделяют верхний квартиль|, который|какой| часто помечают символом 75 % (значит|означает|, что 75 % вариант меньше верхнего квартиль|) и нижний квартиль 25 % (25 % вариант меньше нижнего квартиль|). Т.о.|, три точки — нижний квартиль|, медиана и верхний квартиль — делят выборку на 4 равных части.
Мода (Мо) — величина, которая чаще всего встречается, или чаще всего повторяется. Это варианта, который имеет наибольшую частоту.
Соответствует на графическом изображении максимальной ординате, то есть наивысшему значению графической кривой. При приблизительном определении моды в простом (несгруппированном) ряду она определяется как варианта с наибольшим количеством частот. При этом ряд может иметь бимодальный (два значения случаются с одинаковой частотой) или полимодальный характер.
Отличие медианы и моды от средней арифметической| заключается в том, что эти величины определяются достаточно легко и не зависят от крайних вариант или от степени рассеивания ряда.
Средняя арифметическая часто имеет ограниченное значение потому, что она не отображает размеры колебания количественных вариант ряда (его вариабельность).
Важной характеристикой ряда является оценка разнообразия (изменчивости|переменчивость|, вариабельности|) вариант исследуемой совокупности. Вариацией является изменчивость|переменчивость| только тех признаков, на которые|какие| влияют внешние|наружные| факторы или причины|. Явления, которые изменяются в силу своей природы, нельзя характеризовать как вариацию (изменение|смена| роста ребенка с рождения до|до| совершеннолетия).
Выделяют несколько видов вариации:
-
альтернативная – наличие или отсутствие определенного признака;
-
систематическая – изменение признака в определенном направлении (например, в результате лечения);
- случайная – вариация не имеет явно выраженного направления.
Характеристики разнообразия вариант ряда:
-
амплитуда — разница между крайними значениями. Имеет ограниченное использование в медицине, т.к. не учитывает характер распределения вариант.
-
среднее квадратичное отклонение σ (сигма). Учитывает степень разнообразия всех вариант совокупности относительно средней арифметической и определяется по формуле:
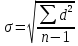 -
для простого вариационного ряда.
-
для простого вариационного ряда.
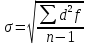 -
для сгруппированного вариационного
ряда.
-
для сгруппированного вариационного
ряда.
где n — число наблюдений в совокупности (при n > 30 вместо n —1 используется n); f— частота вариант; d = х - X — отклонение каждой варианты от средней арифметической; х — значение варианты.
Практическое использование среднего квадратичного отклонения:
-
для определения амплитуды ряда;
-
восстановление его предельных значений;
-
определение возможного числа наблюдений в определенных интервалах.
Величина амплитуды для вариационного ряда с нормальным распределением вариант приблизительно равняется шесть сигмам, поэтому чем выше значение среднего квадратичного отклонения, тем выше степень разнообразия признаков совокупности и менее типична средняя.
Интервал оценки показателей
в
пределах
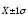 в большинстве случаев определяет их
средний уровень;
в большинстве случаев определяет их
средний уровень;
в
пределах
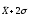 - выше или ниже средних;
- выше или ниже средних;
в
пределах
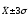 - очень высокие или очень низкие уровни
показателей
- очень высокие или очень низкие уровни
показателей
Правило нормального распределения вариант в вариационном ряду можно определить как правило трёх сигм (Х± 3σ) — относительно средней арифметической практически все варианты совокупность находится в диапазоне ± 3σ. Схематично это можно отобразить так:
Согласно
теории статистики, в пределах X ±
1σ будут находиться не менее 68,37 % всех
вариант совокупности. В пределах X ±
2σ
будут
расположены около 95,45 % всех вариант.
Практически весь вариационный ряд —
99,7 % вариант будет находиться в диапазоне
X ±
3σ.
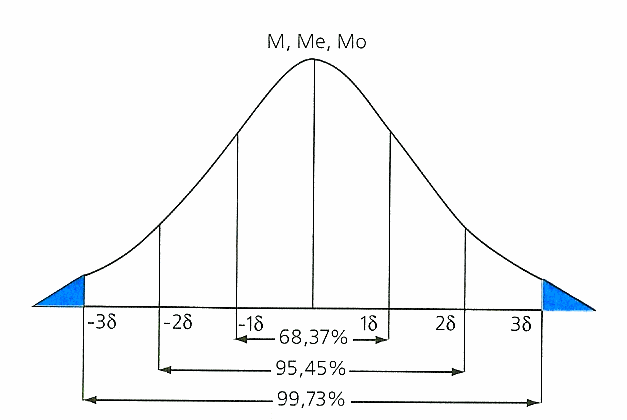
Для вышеуказанных условий значения средней арифметической моды и медианы будут одинаковыми.
Среднее квадратичное отклонение (как мера вариации), возведенное в квадрат, называется дисперсией.
Дисперсия — это средняя величина квадратов отклонений вариант от средней арифметической. Данный показатель также используется в медицине и биологии для характеристики однородности исследуемой совокупности.
При малых значениях σ средняя арифметическая достаточно полно характеризует совокупность (является типичной), тогда как большое значение σ свидетельствует о неоднородности вариационного ряда (нетипичность средней).
В медицине при разработке критериев нормы часто принимается диапазон X ± 1σ (реже X ± 1,5 σ).
С помощью σ можно оценить «выскакивающие» (нетипичные) варианты:

В случае, когда результат выше 3 — данную варианту целесообразно исключить из последующего анализа.
На практике иногда возникает потребность сравнить степень однородности (разнообразие) разных параметров совокупности. Среднее квадратичное отклонение — именная величина, потому непосредственно сравнивать средние квадратичные отклонения вариационных рядов с разными единицами измерения (длина в сантиметрах, вес в килограммах) нельзя.
-
Для обеспечения сопоставления необходимо определить для каждого ряда коэффициент вариации (С) — отношение среднего квадратичного отклонения (сигмы) к средней арифметической в процентах. Данный показатель является относительной мерой вариабельности, что выражается в процентах, а не именуемых числах:

Чем выше коэффициент вариации, тем больше вариабельность данного признака. Критерием в данном случае является такая оценка:
С < 10 % — низкий уровень вариабельности;
С = 10 - 25 % — средний уровень вариабельности;
С > 25 % — высокий уровень вариабельности свидетельствует о невозможности использования данной совокупности для анализа, необходимость расчета по групповых средних или исключения отдельных «выскакивающих» вариант.
