
Информатика / Оптимизация_в_экономике
.pdfТема 16. Задачи оптимизации в экономике и их решение с помощью инструмента Поиск решения
Цель занятия: Рассмотрение различных задач оптимизации, их математических моделей их решения с использованием возможностей средства Поиск решения
С оптимизационными задачами сталкиваются не только менеджеры, экономисты, финансисты, решая задачи планирования штата сотрудников, фонда зарплаты, составления оптимальных планов производства, планированием рекламных компаний, компаний по продвижению продукции на рынок, оптимизацией капиталовложений и т. п., но и каждый из нас в повседневной жизни, решая проблему: как максимально удовлетворить потребности соизмеряясь с имеющимися возможностями.
Составление экономико-математических моделей оптимизационных задач является для экономистов отличной возможностью повышения качества работы.
Для различных задач оптимизации Excel предлагает гибкий инструмент их решения — средство поиска решения. Для его применения требуется умение записать математическую модель задачи и ввести ее, а оптимальное решение будет найдено с помощью инструмента Поиск решения.
16.1. Линейная оптимизационная задача
Линейные оптимизационные задачи можно интерпретировать следующим образом:
Найти максимальное (минимальное) значение линейной оптимизационной функции при линейных ограничениях на переменные. Линейная функция, экстремум которой ищется, называется целевой функцией.
Типичными линейными оптимизационными задачами являются задачи планирования производства, составления смесей, планирования штатного расписания т.п. Рассмотрим в качестве примера задачу составления оптимального плана производства задачу планирования рекламной компании туристической фирмы.
1
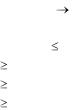
16.1.1. Планирование рекламной компании
Туристическая фирма имеет возможность рекламировать свои услуги, используя местные радио и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены суммой 1 000 $ в месяц. Каждая минута радиорекламы обходится в 5 $, а каждая минута телерекламы обходится в 100 $. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем телевидение. Опыт прошлых лет показал, что каждая минута телерекламы обеспечивает увеличение спроса на услуги в 25 раза большее, чем одна минута радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио и телерекламой.
Составим экономико-математическую модель задачи. Обозначим через xр и xт соответственно время (минут), отводимое ежемесячно на радио и телерекламу. Тогда целевая функция задается линейной функцией
f = xр + 25xт |
max; |
(1) |
|
при ограничениях |
|
|
|
5xр + 100xт |
1000; |
(2) |
|
xр |
2xт; |
|
(3) |
xр |
0; |
|
(4) |
xт |
0. |
|
(5) |
Данная модель является линейной, поскольку и ограничения, и целевая функция линейно зависят от переменных.
Решим задачу с помощью средства Поиск решения.
1. На листе1 введем ограничения задачи (желтым цветом выделены рассчитываемые значения). Значения переменных xр и xт находятся в ячейках A3 и B3 соответственно, значение целевой функции (1) в виде формулы задано в ячейке C5, значения ограничений в виде формул
(2) – (5) заданы в ячейках C7 : D10.
2
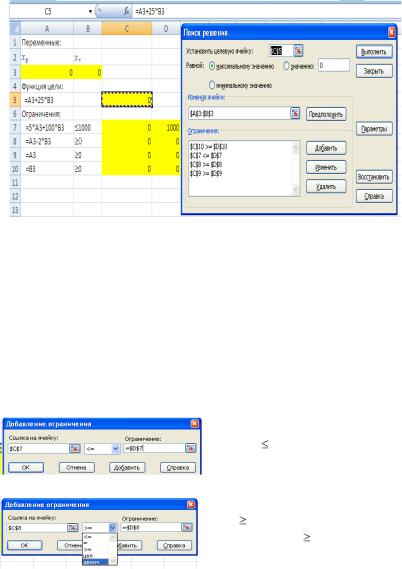
2. Выполнить поиск оптимального решения: Данные| Поиск решения
(Сервис| Поиск решения). Если отсутствует команда Поиск решения
(Solver), то для ее установки необходимо выполнить команду Главная|
|Параметры Excel| Надстройки| Поиск решения (Сервис| Надстройки| Поиск решения).
2.1.Установить целевую ячейку, задав ссылку на ячейку C5 как на ячейку, содержащую значение целевой функции
2.2.Установить целевую ячейку Равной (нажать, если необходимо, ) максимальному значению
2.3.В Изменяя ячейки задать ссылку на диапазон A3 : B3
2.4.Ввести ограничения (2)–(5) задачи.
2.4.1.Для ввода ограничения (2) выполнить :Ограничения| До-
бавить| Ссылка на ячейку|
C7| | Ограничение| D7|
Добавить
2.4.2. Для ввода ограничения (3) выполнить :Ограничения| Доба-
вить| Ссылка на ячейку| C8|
| Ограничение| D8| Доба-
вить. Знак следует выбрать из списка, который раскрывается при нажатии кнопки
3
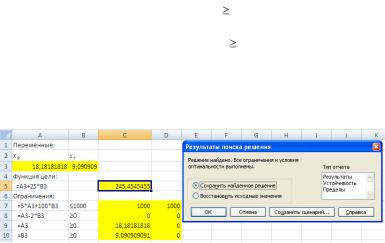
2.4.3. Для ввода ограничения (4) выполнить :Ограничения| Доба-
вить| Ссылка на ячейку| C9| | Ограничение| D9| Добавить
2.4.4. Для ввода ограничения (5) выполнить :Ограничения| Доба-
вить| Ссылка на ячейку| C10| | Ограничение| D10| ОК
2.5.Целевая функция и ограничения заданы, можно выполнять поиск оптимального решения. Для этого нажать на вкладке Поиск решения| Выполнить. После этого открывается окно Результаты поиска решения, которое сообщает, что решение найдено.
2.6. Результаты расчета нашей задачи находятся в ячейках
A3 : B3, а оптимальное значение целевой функции находится в ячейке C5. В соответствии с найденным оптимальным решением следует оплатить 18,18 минут эфирного времени на радио и 9,09 минут на телевидении. Получаемая при этом прибыль составит 245,45 денежных единиц. Данная величина прибыли умножается на стоимость прибыли, приносимой рекламой 1 минутой радиорекламы, например, при стоимости этой прибыли 10$ прибыль составит 2454,5$. Ясно также, что если прибыль 1 минуты радиорекламы составляет меньше 4,07$, то такая рекламная акция не принесет выгоды, поскольку расходы на нее превысят прибыль.
2.7.
2.8. Полученные результаты не являются целочисленными, хотя по смыслу задачи они должны удовлетворять условию целочисленности. В связи с этим к модели задачи (1)– (5) необходимо добавить два условия:
xр — целое; |
(6) |
xт — целое. |
(7) |
2.9. Для выполнения расчета необходимо ввести два новых дополнительных ограничения:
4
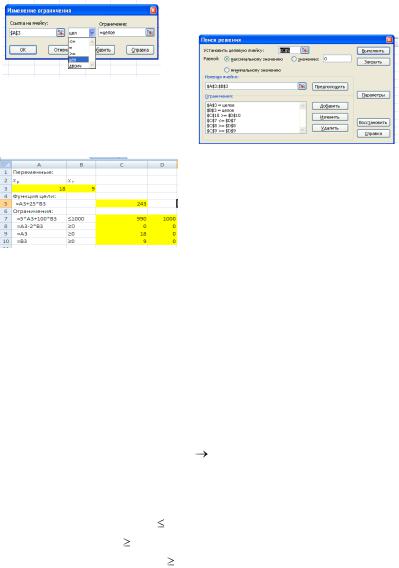
2.9.1. Для ввода ограничения (6) выполнить: Ограничения| Доба-
вить| Ссылка на ячейку| A3| Целое| Добавить
2.9.2. Для ввода ограничения (7) выполнить: Ограни-
чения| Добавить| Ссылка на ячейку| B3| Целое| ОК
2.10. Выполнить поиск це-
лочисленного оптимального решения. Предварительно желательно в ячейки A3 : B3 ввести начальные нулевые значения. Для поиска оптимального плана нажать на вкладке Поиск ре-
шения| Выполнить. После этого от-
крывается окно Результаты поиска решения, которое сообщает, что решение найдено.
2.11. Результаты расчета, находящиеся в ячейках A3 : B3, показывают, что в соответствии с найденным оптимальным решением следует оплатить 18 минут эфирного времени на радио и 9 минут на телевидении. Получаемая при этом прибыль составит 243 денежные единицы. При этом на проведение рекламной компании будет израсходовано, как следует из содержимого ячейки C7, 990$ (а не вся сумма в 1000$).
3. Сохранить документ как книгу Excel: Файл| (Кнопка «Office»)
Сохранить| Сохранить как| Книга Excel|Задать имя| ОК.
Упражнение 16.1.
Используя средство Поиск решения, найти оптимальное решение задачи:
f = x1 + x2 – x3 – 2x5 min
при ограничениях
x1 – 2x2 + x4 = –3;
x3 |
– 2x4 = 2; |
|
2 x2 – x4 + x5 |
5; |
|
x2 |
+ x5 –3; |
|
x1, x2, x3, x4, x5 |
0 |
|
5

Упражнение 16.2.
Используя средство поиск решения, найти оптимальное целочисленное решение следующей. задачи:
f = 2x1 + x2 + x3 |
max |
при ограничениях
x1 + 2x2 +2 x3 = 16; x1 + x2 7;
3 x1 + 2 x3 18;
x1, x2, x3, x4, x5 = 0, или 1, или 2, …
16.2. Транспортная задача
Транспортные оптимизационные задачи можно интерпретировать следующим образом:
В m пунктах производства A1, A2, …, Am находится однородный продукт в количествах a1, a2, …, am, который нужно доставить n потребителям B1, B2, …, Bn в количествах b1, b2, …, bn. Известны расходы, связанные с перевозкой единицы продукции из пункта Ai в пункт Bj. Требуется составить оптимальный план перевозок, минимизирующий транспортные издержки и обеспечивающий спрос всех потребителей за счет распределения всей произведенной продукции.
Многие задачи в математическом отношении подобны транспортной, так как описываются аналогичной: задачи оптимального размещения производственных объектов, в которых целевая функция рассматривается как сумма затрат на производство и транспортировку; задачи об оптимальном распределении производства между хозяйственными объектами, о рациональном закреплении механизмов за определенными видами работ, о распределении посевных площадей и т.п. В некоторых задачах транспортного типа целевая функция максимизируется.
Рассмотрим в качестве примера задачу транспортную задачу оптимизации перевозки туристов.
6
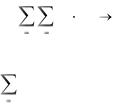
16.1.1. Планирование перевозки туристов
Туристическая фирма занимается отправкой туристов в страны отдыха авиатранспортом. Стоимость перевозки (условная) одного пассажира до пункта назначения и обратно различными авиакомпаниями задана в таблице 1. Задано число место, которые можно забронировать в различных рейсах. Задано также общее число мест в гостиницах, которые можно забронировать для отдыхающих. Необходимо составить план перевозок по доставке туристов, минимизирующий суммарные транспортные расходы.
|
Черно- |
Тур- |
Еги- |
Пор |
Ита |
Число мест |
|
гория |
ция |
пет |
туга |
лия |
в самоле- |
|
|
|
|
га- |
|
тах, Bj |
|
|
|
|
лия |
|
|
Белавиа |
530 |
620 |
710 |
580 |
480 |
70 |
|
|
|
|
|
|
|
Австрийские |
520 |
595 |
690 |
610 |
510 |
20 |
авиалинии |
|
|
|
|
|
|
|
|
|
|
|
|
|
Литовские |
550 |
600 |
750 |
560 |
490 |
30 |
авиалинии |
|
|
|
|
|
|
|
|
|
|
|
|
|
Чешские авиа- |
500 |
630 |
700 |
590 |
520 |
40 |
линии |
|
|
|
|
|
|
Число мест в |
30 |
60 |
20 |
20 |
30 |
|
гостиницах, Ai |
|
|
|
|
|
|
Составим экономико-математическую модель задачи. Обозначим через xij число пассажиров, перевозимых i-ой авиакомпанией
(i = 1,…,4) в j–ую страну (j = 1,…,5), а через cij — стоимость перевозки одного пассажира. Тогда целевая функция — это суммарные транс-
портные расходы, т. е.
4 |
5 |
|
|
f = |
cij xij |
min; |
(1) |
i 1 |
j 1 |
|
|
при ограничениях
4
xij = Bj; |
(2) |
i 1
7
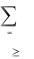
5 |
|
|
|
xij = Ai; |
(3) |
j |
1 |
|
xij |
0; |
(4) |
xij — целые; |
(5) |
|
1. Для решения этой задачи с помощью средства поиска решений ввести данные, как показано на рисунке ниже:
В таблице Тарифы на перевозки (ячейках B2:F5) ввести тарифы на перевозки. Ячейки B9:F12 отведены под значения неизвестных, т. е. числа туристов, перевозимых i-ой авиакомпанией (i = 1,…,4) в j–ую страну (j = 1,…,5). Если не вводить в эти ячейки числовые значения, они будут считаться равными 0.
2.В ячейку G13 ввести целевую функция
=суммпроизв(B2:F5; B9:F12).
3.В ячейках B13:F13 ввести формулы
=сумм(B9:B12), =сумм(C9:C12), =сумм(D9:D12), =сумм(E9:E12), =сумм(F9:F12),
определяющие число мест в гостинице, занимаемых туристами. 4. В ячейках G9:G12 ввести формулы
=сумм(B9:F9), =сумм(B10:F10), =сумм(B11:F11), =сумм(B12:F12),
определяющие число мест, бронируемых в соответствующих авиакомпаниях.
5. Выполнить поиск оптимального решения:
Данные| Поиск решения (Сервис| Поиск решения).
Проверить, нажав кнопку Параметры, установлена ли линейная модель. Ограничения по строкам и столбцам вводятся как массивы.
8
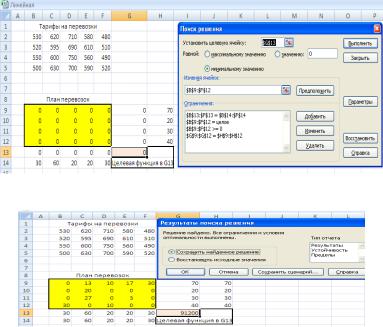
6. После нажатия кнопки Выполнить средство поиска решения находит оптимальный план перевозки туристов.
7.Результаты расчетов помещаются в ячейки B9:F12, а значение целевой функции находится в ячейке G13.
Из результатов расчета мы видим, что минимальные транспортные расходы, составляющие 91 200 условных единиц, соответствуют следующему плану отправки туристов: самолеты Белавиа перевозят 13 пассажиров в Турцию, 10 в Египет, 17 в Португалию и 30 в Италию. Самолеты Австрийских авиалиний перевезут 20 пассажиров в Турцию
исамолеты Литовских авиалиний перевезут в Турцию 27 пассажиров. Самолеты Чешских авиалиний доставят 30 туристов в Черногорию и 10 туристов в Египет.
8.Сохранить документ в своей папке.
Упражнение 16.3.
Используя средство Поиск решения, найти оптимальное решение следующей транспортной задачи:
9
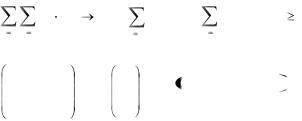
|
3 |
4 |
|
|
3 |
|
|
4 |
|
f = |
|
|
cij |
xij |
min; |
xij |
= Bj; |
xij |
= Ai; xij 0; xij — це- |
i |
1 |
j 1 |
|
i |
1 |
|
j 1 |
|
|
лые; |
|
|
|
|
|
|
|
|
|
|
6 |
7 |
3 |
5 |
100 |
|
= 75 |
80 |
60 85 . |
cij = |
1 |
2 |
5 |
6 ; |
Bj = 150 ; ai |
||||
|
3 10 |
20 |
1 |
50 |
|
|
|
|
|
Упражнение 16.4.
Используя средство Поиск решения, составить экономикоматематическую модель и найти оптимальное решение транспортной задачи, числовые значения которой заданы в таблице:
|
|
|
|
|
Bj |
|
2 |
3 |
5 |
4 |
30 |
|
3 |
2 |
4 |
1 |
40 |
|
|
|
|
|
|
|
4 |
3 |
2 |
6 |
20 |
|
|
|
|
|
|
Ai |
20 |
25 |
35 |
10 |
90 |
Упражнение 16.5. Задача о назначениях.
Имеются n рабочих и m видов работ. Стоимость cij выполнения i-ым рабочим j-ой работы приведена в таблице, где рабочему соответствует строка, а работе — столбец. Необходимо составит план работ так, чтобы все работы были выполнены, каждый рабочий был занят только на одной работе, а суммарная стоимость выполнения всех работ была бы минимальной.
Стоимость выполнения работ
|
|
|
Виды работ |
|
||
|
|
|
|
|
|
|
рабо- |
3 |
6 |
2 |
5 |
11 |
|
|
|
|
|
|
||
1 |
2 |
7 |
11 |
3 |
||
чие |
||||||
|
|
|
|
|
||
5 |
12 |
11 |
9 |
1 |
||
|
||||||
|
|
|
|
|
|
|
|
2 |
4 |
2 |
10 |
5 |
|
|
|
|
|
|
|
|
Используя средство Поиск решения, составить экономикоматематическую модель и найти оптимальное решение задачи о назначениях.
10
