
- •«Точка в 3d пространстве»
- •Оглавление
- •Содержательная и формальная постановка задачи
- •Содержательная постановка задачи.
- •Формальная постановка задачи.
- •Краткие теоретические сведения
- •Отрисовка (вывод чертежей на экран).
- •Укрупнённый алгоритм
- •Ввод данных.
- •Вычисления.
- •А) Вычисления координат для пространственного чертежа.
- •Детализированный алгоритм
- •Ввод данных.
- •Вычисления. А) Вычисления координат для пространственного чертежа.
- •Б) Вычисление координат для комплексного чертежа.
- •Отрисовка (вывод чертежей на экран). А) Отрисовка пространственного чертежа.
- •Б) Отрисовка комплексного чертежа.
- •Руководство программиста
- •Руководство пользователя
- •Заключение
Федеральное Государственное бюджетное образовательное учреждение
Высшего профессионального образования
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра ВМиК
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
по лабораторной работе № 1
«Точка в 3d пространстве»
по дисциплине «Компьютерная графика»
Выполнил:
Студент группы МО-305
Горбатов В.А.
Проверил:
Профессор кафедры ВМиК
Верхотуров М.А.
Уфа 2016
Оглавление
Оглавление 1
1.Содержательная и формальная постановка задачи 3
1.1.Содержательная постановка задачи. 3
1.2.Формальная постановка задачи. 3
2.Краткие теоретические сведения 4
4.3Отрисовка (вывод чертежей на экран). 12
5.1Укрупнённый алгоритм 15
5.1.1Ввод данных. 15
5.1.2Вычисления. 15
а) Вычисления координат для пространственного чертежа. 15
б) Вычисление координат для комплексного чертежа. 16
5.1.3Отрисовка (вывод чертежей на экран). 16
а) Отрисовка пространственного чертежа. 16
б) Отрисовка комплексного чертежа. 16
5.2 Детализированный алгоритм 17
5.2.1Ввод данных. 17
5.2.2Вычисления. 17
а) Вычисления координат для пространственного чертежа. 17
б) Вычисление координат для комплексного чертежа. 18
5.2.3Отрисовка (вывод чертежей на экран). 18
а) Отрисовка пространственного чертежа. 18
б) Отрисовка комплексного чертежа. 19
6.Руководство программиста 21
При запуске программы создаются экземпляры класса Point3D, Point, массивы точек points3D, points3D_disp, pointsComplex_disp в конструкторе Form1. В методе input() заполняется массив points3D. После инициализации вызываются методы перерасчета координат чертежей. Для пространственного чертежа перевод в систему экрана происходит в методе Area(): значения записываются в массив points3D_disp, который использует функцию перерасчета Projection3D(points3D[i]), где в качестве параметров в функцию передаются элементы массива points3D. Для комплексного чертежа перевод в систему экрана происходит в методе Complex(): значения записываются в массив pointsComplex_disp, который использует функцию перерасчета ProjectionComplex(x,y), где в качестве параметров в функцию передаются элементы массива points3D. Далее происходит прорисовка для показа первоначального чертежа в pb3D и pbComplex с помощью функций Draw3D(), DrawComplex() соответственно. 24
7.Руководство пользователя 25
Заключение 26
Содержательная и формальная постановка задачи
Содержательная постановка задачи.
Содержание экрана:
пространственный чертеж с изображением точки T, ее проекций на координатные плоскости T1, T2, T3 и ее проекций на координатные оси TX, TY, TZ, а также линий связи;
комплексный чертеж с изображением проекций точки T – T1, T2, T3, а также линий связи;
ползунковые переключатели для интерактивного изменения координат точки T и угла между осями Ox и Oy на пространственном чертеже.
Динамика:
при изменении координат точки T должны изменяться ее изображение, изображения ее проекций и линий связи как на пространственном, так и на комплексном чертежах;
при изменении угла между осями Ox и Oy пространственный чертеж должен перерисовываться.
Формальная постановка задачи.
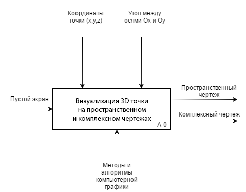
Краткие теоретические сведения
В основу построения любого изображения положена операция проецирования.
Сущность метода ортогонального проецирования заключается в том, что предмет проецируется на две взаимно перпендикулярные плоскости лучами, ортогональными (перпендикулярными) к этим осям.
Одну из плоскостей проекций П1 располагают горизонтально, а вторую П2 - вертикально. Плоскость П1 называют горизонтальной плоскостью проекций, П2 - фронтальной. Плоскости П1 и П2 бесконечны и непрозрачны.
При построении проекций необходимо помнить, что проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. Проекцию точки T на горизонтальную плоскость называют горизонтальной проекцией и обозначают T1, проекцию точки T на фронтальную плоскость - фронтальной проекцией и обозначают T2. Каждая из них является основанием перпендикуляра, опущенного из данной точки T соответственно на плоскости П1 и П2. Две проекции точки определяют ее положение в пространстве. Так как каждая фигура или тело представляет собой совокупность точек, то можно утверждать, что две ортогональные проекции вполне определяют его форму.
Однако в практике изображения строительных конструкций, машин и различных инженерных сооружений возникает необходимость в создании дополнительных проекций. Чтобы сделать проекционный чертеж более ясным и удобочитаемым, используют третью плоскость, перпендикулярную П1 и П2. Эта плоскость обозначается буквой П3 и называется профильной. Проекцию точки T на плоскость П3 называются профильной и обозначают T3.
Плоскости проекций, попарно пересекаясь, определяют три оси: Ox, Oy и Oz, которые можно рассматривать как систему прямоугольных декартовых координат в пространстве с началом в точке O. Три плоскости проекций делят пространство на восемь трехгранных углов - это так называемые октанты. Нумерация октантов дана на Рис. 1.
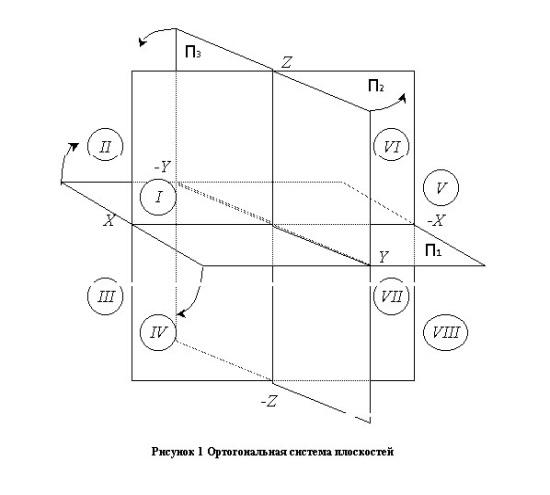 Рис.
1 – Нумерация октантов.
Рис.
1 – Нумерация октантов.
Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первом октанте. Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещены определенным образом одна с другой, называется эпюром Монжа (просто эпюром или комплексным чертежом). Для получения эпюра плоскости П1 и П3 вращают как показано на Рис. 1, до совмещения с плоскостью П2. В результате вращения передняя полуплоскость П1 оказывается совмещенной с нижней полуплоскостью П2, а задняя полуплоскость П1 – с верхней полуплоскостью П2. Окончательный вид всех совмещенных плоскостей проекций дан на Рис. 2.
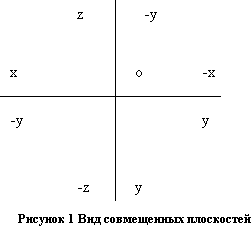 Рис.
2 – Эпюр Монжа.
Рис.
2 – Эпюр Монжа.
Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности.
В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x, y, z. Абсцисса x определяет расстояние от данной точки до плоскости П3, ордината y – до плоскости П2 и аппликата z – до плоскости П1.
Построение изображения самой точки и ее проекций на пространственной модели рекомендуется осуществлять с помощью координатного прямоугольного параллелепипеда. Прежде всего на осях координат от точки O откладывают отрезки, соответственно равные единицам длины. На этих отрезках (OTX, OTY, OTZ), как на ребрах, строят прямоугольный параллелепипед. Вершина его, противоположная началу координат, и будет определять заданную точку T.
Построение параллелепипеда позволяет определить не только точку T, но и все три ее ортогональные проекции.
Лучами, проецирующими точку на плоскости П1, П2 и П3, являются те три ребра параллелепипеда, которые пересекаются в точке T.
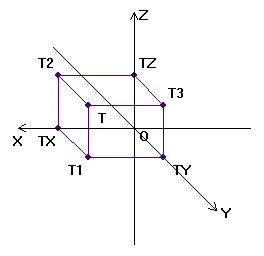 Рис.
3 – Пространственный макет точки T.
Рис.
3 – Пространственный макет точки T.
На эпюре, где все плоскости проекций совмещены, проекции T1 и T2 окажутся на одном перпендикуляре к оси OX, а проекции T2 и T3 - на одном перпендикуляре к оси OZ. Что касается проекций T1 и T3, то и они связаны прямыми T1TY и T3TX, перпендикулярными оси OY. Но так как эта ось на эпюре занимает два положения, то отрезок T1TY не может быть продолжением отрезка T3TY.
Построение проекций точки T на эпюре по заданным координатам выполняют в такой последовательности: прежде всего на оси абсцисс от начала координат откладывают отрезок OTX = x, а затем через точку TX проводят перпендикуляр к оси Ox, на котором с учетом знаков откладывают отрезки TXT1 = y (получаем T1) и TXT2 = z (получаем T2). Остается построить профильную проекцию точки T3. Так как профильная и фронтальная проекции точки должны быть расположены на одном перпендикуляре к оси Oz, то через T2 проводят прямую T2TZ перпендикулярно Oz. Наконец, возникает последний вопрос: на каком расстоянии от оси Oz должна находиться T3? Рассматривая координатный параллелепипед, ребра которого TZT3 = OTY = TXT1 = y, заключаем, что искомое расстояние TZT3 равно y. Отрезок TZT3 откладывают вправо от оси Oz, если y > 0, и влево, если y < 0.
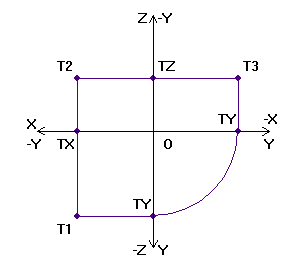 Рис.
4. – Комплексный чертеж точки T.
Рис.
4. – Комплексный чертеж точки T.
Структура решения (этапы решения и их взаимосвязь)
Ввод данных (координаты точки Т и угол наклона оси ОY);
Вычисления;
Вычисление координат точек и линий проекций для пространственного чертежа;
Вычисление координат точек и линий проекций для комплексного чертежа.
Отрисовка.
Отрисовка пространственного чертежа;
Отрисовка комплексного чертежа.
Обзор и анализ методов решения
Ввод данных(координаты точки Т и угол наклона оси ОY)
Прежде всего необходимо ввести в программу информацию о координатах точки и угле наклона оси ОY.
Для ввода угла и координат точки пользователю будет удобнее использовать непрерывный компонент, который представляет собой элемент управления в виде ползунка, который можно перемещать курсором мыши во время выполнения. В платформе .NET этот элемент называется TrackBar.
Обобщенный алгоритм:
Считать входные данные (координаты точки Т, угол между осями Ox и Oy) с ползунковых переключателей.
Записать эти данные в соответствующие переменные.
Вычисления. Для построения чертежей на экране нам необходимо уметь переводить координаты из реальной трехмерной системы координат в двумерную систему координат экрана (для пространственного чертежа), а также определять по трехмерным координатам координаты на комплексном чертеже и переводить их в двумерную систему координат экрана.
Вычисление координат для пространственного чертежа.
Входные данные:
координаты T точки в трехмерной декартовой системе координат пространства – x, y, z
угол angle между положительным направлением оси Oy и отрицательным направлением оси Ox на пространственном макете
ширина и высота чертежа – width и height.
Выходные данные:
экранные координаты точек системы координат
экранные координаты точки T (X,Y,Z);
экранные координаты ее проекций на плоскости П1, П2, П3 – T1, T2, T3;
экранные координаты ее проекций на координатные оси – TX, TY, TZ;
(width,0) (0,0)
(width,height) (0,height)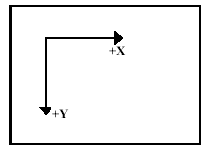 Рис.
5. – Экранная система координат.
Рис.
5. – Экранная система координат.
(1)
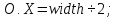
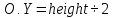
Таким образом, нужно вывести формулы для перевода заданных трехмерных координат произвольной точки T x, y, z в экранные двумерные координаты xэ, yэ, учитывая заданный угол angle и координаты начала отсчета – x0, y0.
Рассмотрим следующий рисунок.
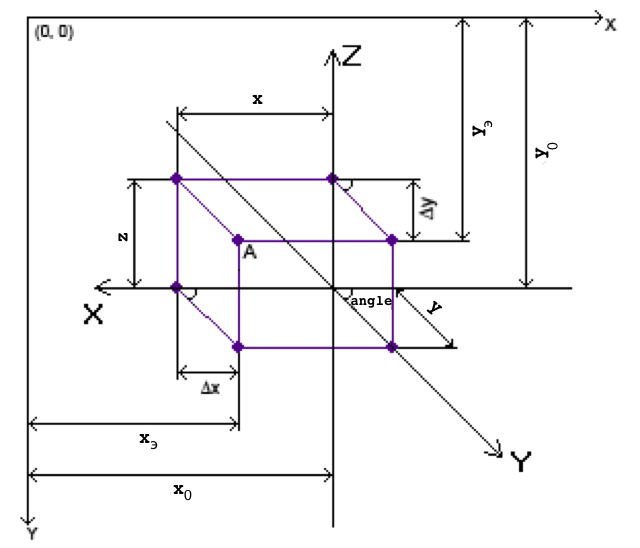 Рис.
6. – Нахождение экранных координат
произвольной точки A.
Рис.
6. – Нахождение экранных координат
произвольной точки A.
Из этого
рисунка видно, что
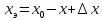 и
и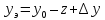 ,
где ∆x
и ∆y
находятся из соответствующих прямоугольных
треугольников по формулам:
,
где ∆x
и ∆y
находятся из соответствующих прямоугольных
треугольников по формулам:
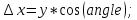
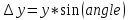
(2)
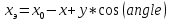
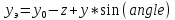
Итак, мы получили формулы для вычисления экранных координат произвольной точки по заданным трехмерным координатам, углу angle и координатам начала отсчета. По этим формулам можно вычислить координаты точек, необходимых для построения пространственного чертежа - T, T1, T2, T3, TX, TY, TZ.
Обобщенный алгоритм:
Вычислить экранные координаты точки начала отсчета пространственного чертежа по формулам (1);
Вычислить координаты самой точки, её проекций на координатные оси и плоскости П1, П2, П3 по формулам (2).
Вычисление координат для комплексного чертежа.
Входные данные:
координаты точки T в трехмерной декартовой системе координат – x, y, z
ширина и высота чертежа – w и h.
Выходные данные:
экранные координаты начала отсчета комплексного чертежа;
координаты точек комплексного чертежа: T1, T2, T3 (проекции точки T на П1, П2, П3), Tx, Ty1, Ty2, Tz (проекции точки T на оси, для оси Y – две такие точки, т.к. на комплексном чертеже она представлена дважды).
Координаты начала отсчета x0, y0 находятся по формуле (1).
Рассмотрим следующий рисунок, расстояния x, y, z на котором обозначены в соответствии с построением комплексного чертежа.
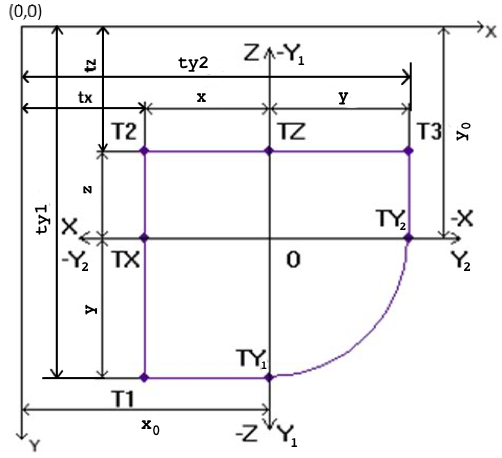 Рис.
7. – Нахождение экранных координат точек
для построения комплексного чертежа.
Рис.
7. – Нахождение экранных координат точек
для построения комплексного чертежа.
(3)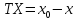
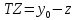
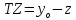
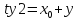
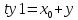
Заметим, что координаты всех интересующих нас точек можно найти из значений x0, y0, tx, tz, ty1, ty2:
(4)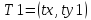
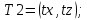
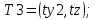
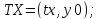
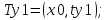
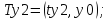
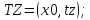
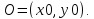
Обобщённый алгоритм:
вычислить координаты начала отсчёта по формулам (1).
вычислить временные переменные по формулам (3).
вычислить координаты проекций точки по формулам (4).
