Верхотуров / билеты 2015

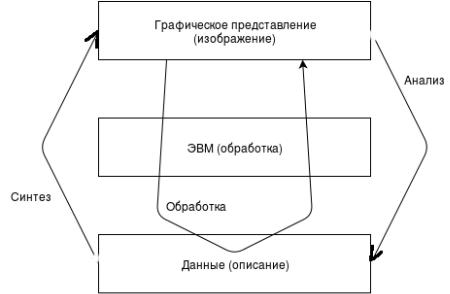
1Определение понятия маш.граф. Области ее применения

Компьютерная графика - это совокупность методов и средств, используемых для преобразования данных в графическую форму представления и из графической формы представления с помощью ЭВМ.

Основные компоненты: данные, ЭВМ и графическая форма представления. Причины применения: компьютерная графика является наиболее гибким и мощным

средством взаимодействия между человеком и ЭВМ.

Достоинства маш. графики: сложные информационные структуры и взаимосвязи осознаются человеком за более короткий промежуток времени в большем объеме и с меньшими искажениями.

В зависимости от направления, в котором преобразуются и передаются данные (по отношению к ЭВМ), способы их визуального представления и типы объектов, которыми манипулирует графическая система, различают три области применения компьютерной графики: синтез, анализ и обработка изображений.

Классифицируюшие параметры для задач синтеза, анализа и обработки изображений можно изобразить в виде следующей таблицы:

1

При синтезе данные могут поступать от источников первичного ввода, быть результатами произведенных вычислений, быть командами или действиями оператора графической станции.

2

2Пользователи, интерфейсы, стандарты и маш.граф.

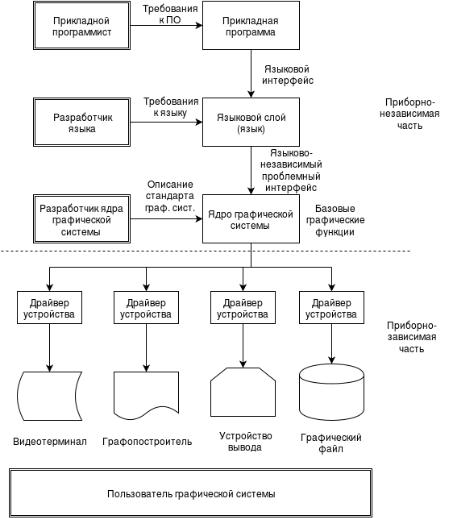
Для стандартизации взаимодействия различных слоёв разработаны соответствующие интерфейсы: языковой интерфейс, языково-независимый проблемный интерфейс, интерфейс графической системы. В качестве стандартов графических системы известны функциональные стандарты GKS, GKS-3D и PHIGS. Так, в частности, GKS был принят в 1985 году. Он предоставляет в распоряжение программиста ряд базовых графических функций, обеспечивающих доступ к графическим устройствам через специальный логический объект - графическую рабочую станцию. Соотвественно, в стандарте GKS-3D содержится набор обобщенных операций над трехмерными элементами, полностью совместимый с двумерной версией стандарта. Интерфейс компьютерной графики (CGI) регламентирует интерфейс между системой, реализующей функциональный стандарт, и графическими устройствами, с которыми она взаимодействует.

Уровень языковой оболочки - функциональные стандарты независимые от языков программирования, используемых при разработке прикладных программ. Для того, чтобы разрабатываемое ПО было переносимым, способ отображения предусмотренных стандартом функций должен быть также стандартным. Стандартные языковые оболочки определяют конкретное представление используемых функциональных стандартов, типов данных и имён функций.

Уровень прикладной программы - прикладные программы разрабатываются с использованием одного из стандартных языков программирования. В текстах программы содержится обращение к граф. процедурам соответвенно синтаксису и семантике, реглам.

3

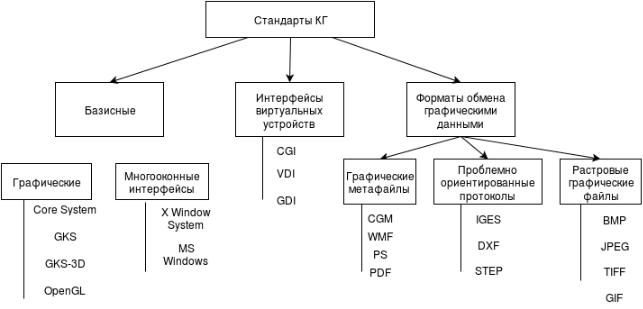
стандартами языковой оболочки. С графическими устройствами прикладная программа взаимодействует только через стендартные функции. Это обеспечивает их независимость как от программного, так и от аппаратного обеспечения конкретной системы КГ.

Рис. 1: Стандарты компьютерной графики

3Основные понятия графической системы

Графические системы служат для создания, поиска, хранения, модификации и вывода графических данных. Графические системы могут быть пассивными и интерактивными. Пассивные системы обеспечивают вывод графических изображений, при этом человек не может прямо воздействовать на графические преобразования. Интерактивные системы дают возможность человеку динамически управлять изображением в режиме диалога. Графические системы применяются при синтезе изображения, анализе изображения и обработке изображения. При синтезе изображения из описания объекта, который составил пользователь, получается геометрическая модель объекта с последующим отображением на экране. Анализ изображения выполняет обратную задачу, т.е. из имеющегося графического изображения получают формальное описание объекта.

Основное назначение графической системы состоит в преобразовании двух или трехмерной модели объекта, который формируется прикладной программой, в графические команды и данные, которые либо передаются на устройства, либо запоминаются в той или иной графической структуре данных.

Графическая система ПК состоит из аппаратной и программной частей. Аппаратная часть включает видеоадаптер, монитор и интерфейсы, которые обслуживают графическую систему. Графическая система используется всеми прикладными программами. Приложение использует функции видеоадаптера при посредничестве драйвера. Драйвер реализует взаимодействие с системой и выполнение элементарных операций на устройстве (перемещение пишущего инструмента графопостроителя, электронного луча графического дисплея, подсветка точки и т.д.).

Графической подсистемой часто считается часть операционной системы, которая обеспечивает решение задач компьютерной графики. В нее входят программные средства ввода, обработки и отображения графической информации, а также преобразование данных

4

в графическую форму. Например, пакет OpenGL для Windows. Графическая подсистема состоит из ядра и обширной библиотеки графических функций.

Графическое ядро является частью графической системы. Графическое ядро имеет собственную систему команд и набор элементарных функций работы с графикой. Графическое ядро реализует определенный набор графических примитивов. Основной функцией графического ядра является поддержка вывода графических примитивов.

Графическое ядро имеет независимую от интерпретатора структуру и реализует следующие функции: рендеринг ландшафтов, полигональных объектов, сфер окружения, освещения, движение тел под действием физических сил, проверка на столкновения, работы с векторами, изменение параметров графического контекста, синхронизация по времени для различных по мощностям компьютеров, реализация внутреннего таймера.

Графический примитив – это простейший геометрический объект, создаваемый и обрабатываемый как единое целое и отображаемый на устройстве вывода. Существуют графические примитивы двухмерной и трехмерной графики, каждый примитив имеет определенный набор атрибутов. Основное значение графических примитивов - обеспечить наличие программных средств для рисования всевозможных геометрических объектов.

Концепция виртуального устройства начала разрабатываться с момента появления аппаратно-независимых графических систем. Интерфейс виртуального устройства разделяет аппаратно-зависимую и аппаратно-независимую части графической системы. Он обеспечивает заменяемость графических устройств (терминальную независимость), а также возможность работы с несколькими устройствами одновременно. Интерфейс виртуального устройства может существовать в форме программного интерфейса и/или протокола взаимодействия двух частей графической системы. Наиболее четко концепция виртуального устройства представлена в проекте стандарта CGI.

4Проецирование. Отображение геометрических объектов на плоскости

КГ появилось на основе достижений кибернетики и начертательной геометрии. Начертательная геометрия - раздел геометрии, в котоором пространственные фигуры изучаются с помощью изображений на плоскости.

Отображение же геометрической фигуры на плоскость (или какую-либо другую поверхность) можно осуществить путем проецирования её точек на эту плоскость (поверхность). Таким образом, в основу построения любого изображения положена операция проецирования, которая заключается в следующем: имеет плоскость проекции i (картинная плоскость), для которой хотим получить изображение оригинала, точки А. Операция проецирования заключается в проведенеии через точку A прямой, которая называется проецирующей. Точкак же Ai (пересечение проецирующей прямой с плоскостю i) как раз и называется проекцией точки А на плоскость i. Для определения в пространстве проецирующей прямой зададим точку S (S не совпадает с A), через которую проходят все проецирующие прямые. Точка S при этом называется центром проецирования, операция, в этом случае, называется центральным проецированием, а её результат - центральной проекцией.

Другой способ определение проецирующей прямой - задание вектора ~s непараллельного плоскости i, называемого направлением проецирования. Проецирующие прямые в этом случае строят параллельными вектору ~s, а операция называется параллельным проецированием. Соответственно проекция называется параллельной.

В случае параллельного проецирования проецирующие прямые наклоненые по отношению к плоскости проекции i под углом . Если угол 6= 90 , то проецирование называется

5

косоугольным, когда же угол = 90 , то проецирование называется прямоугольным (ортогональным), а проекция также называется прямоугольной (ортогональной).

5Дополнение Евклидова пространства. Ортогональное проецирование и его свойства

Внекоторых случаях возникат нарушение соответствия, устанавливаемого проецированием между точками точками оригинала и проекции. Для устранения такого несоответствия существуют определенные меры. Операцию центрального проецирования мы рассматриваем в евклидовом пространстве, в котором параллельные прямые не перескаются. Условимся считать параллельные прямые пересекающимися в бесконечно удаленной (несобственной) точке. Таким образом каждая прямая дополняется несобственной точкой, а каждая плоскость дополняется несобственной прямой. Их совокупность порождает несобственную плоскость. Таким образом пространство, дополненное несобственными элементами (точками, прямыми и плоскостью) называется дополнением евклидова пространства. И соответственно это дополнение евклидова пространства приводит к тому, что устанавливается соответствие между точками оригинала и их проекциями.

Всвязи с тем, что каждая точка пространства при заданном аппарате проецирования будет иметь одну и только одну проекцию, а обратно утверждение не имеет места, то для определения положения точки в пространстве (обратимости задачи) необходимо иметь две ее центральные или параллельные проекции, полученные при двух различных центрах проекций (или направления проецирования)

Ортогональное проецирование - это частный случай параллельного проецирования, при котором направление проецирования перпендикулярно плоскости проекции. Ортогональное проецирование обладает рядом преимуществ перед центральным и параллельным (косоугольным) видами проецирования. К ним, в первую очередь, следует отнести:

1.Простоту геометрических построений для определения ортогональных проекций точки.

2.Возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. Отсюда вытекают два важных свойства:

(a)Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.

(b)Для того, чтобы прямой угол проецировался ортогонально без искажения необходимо и достаточно, чтобы, по крайней мере одна его сторона была параллельна плоскости проекций, а вторая сторона не перпендикулярна к этой плоскости.

6Пространственная и плоскостная модели координатных плоскостей проекций

Для того, чтобы получить ортогональный чертеж, обладающий свойством обратимости, необходимо иметь по крайней мере две связанные между собой ортогональные проекции оригинала. Наиболее удобной для фиксирования положения геометрической фигуры в пространстве и выявления её формы по ортогональным проекциям является декартова

6

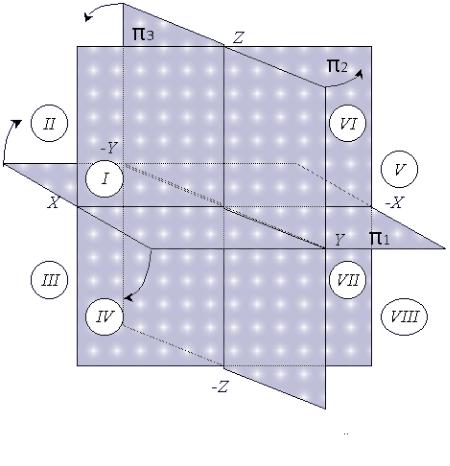
система координат, состоящая из трех взаимно перпендикулярных плоскостей. В основу построения любого изображения положена операция проецирования. Сущность метода ортогонального проецирования заключается в том, что предмет проецируется на две взаимно перпендикулярные плоскости лучами, ортогональными (перпендикулярными) к этим осям.

1 - горизонтальная плоскость.2 - фронтальная плоскость.3 - профильная плоскость.

Рис. 2: Ортогональная система плоскостей

Три плоскости проекций делят пространство на восемь трехгранных углов - это так называемые октанты.

Пользоваться пространственным макетом для отображения ортогональных проекций геометрических фигур неудобно ввиду его громоздкости, а также из-за того, что на плоскостях 1 и 3 происходит искажение формы и размеров проецируемой фигуры. Поэтому вместо изображения на чертеже пространственного макета пользуеются т.н. эпюром Монжа или комплексным чертежом, т.е. чертежом, составленным из двух или более связанных между собой ортогональных проекций геометрической фигуры. Преобразование пространственного макета в комплексный чертеж осуществляется путем совмещения плоскостей 1 и 3 с фронтальной плоскостью проекции 2.

Для совмещения плоскости 1 с 2 поворачиваем её на 90 градусов вокруг оси X в направлении движения часовой стрелки. Профильная плоскость прокций 3 поворачивается вокруг оси Z также на 90 градусов в направлении противоположном движению часовой стрелки.

7

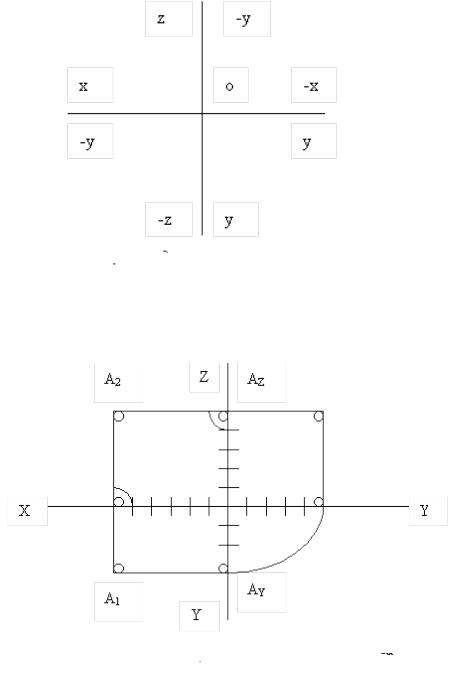
Рис. 3: Вид совмещенных плоскостей

Рис. 4: Проекции точки первого октанта на комплексный чертеж

7Проекции точки

Проекция точки на плоскостьэто либо сама точка, если она лежит в заданной плоскости, либо основание перпендикуляра, опущенного из этой точки на заданную плоскость.

8

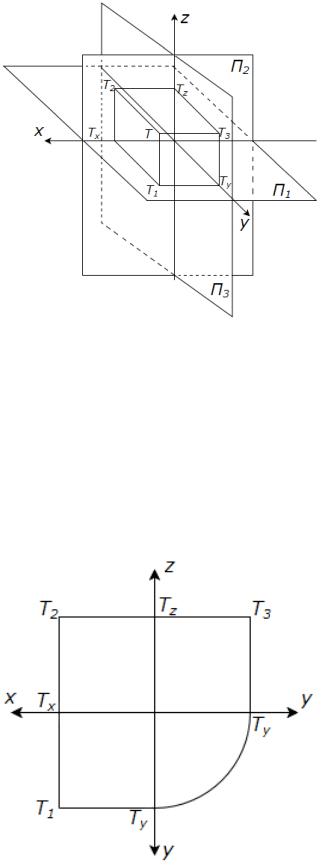
Рис. 5: Пространственный макет точки

Нарисуем пространственный макет точки Т в первом октанте. (Рис. 5)

T1(x,y)- горизонтальная проекция точки T.

T2(x,z)- фронтальная проекция точки T.

T3(y,z)- профильная проекция точки T.

Ниже представлен комплексный чертеж точки.

Рис. 6: Комплексный чертеж точки

9

8Задание прямой линии

Способы задания прямой:

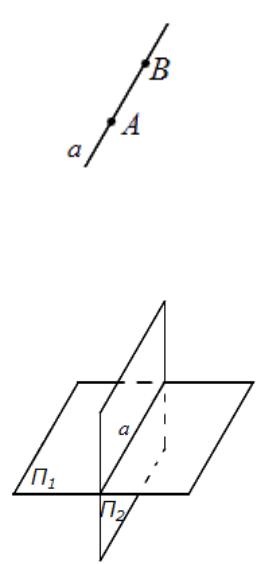
Двумя точками.

Рассмотрим две точки в пространстве, A и B. Через эти точки можно провести прямую линию a.

Двумя плоскостями.

Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии.

Двумя проекциями.

Пусть в плоскостях 1 и 2 даны проекции прямых заданных отрезками [A1; B1] и [A2; B2]. Проведем через эти прямые плоскости и перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные, линией их пересечения будет прямая заданная отрезком [A; B], проекциями которой являются отрезки

[A1; B1] и [A2; B2].

10