
Кристаллография
.pdf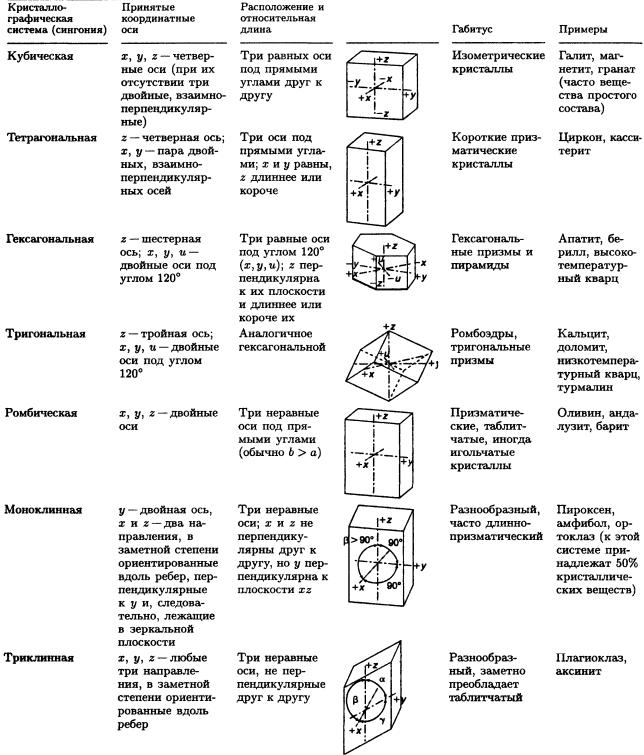
Таблица 3.3 Кристаллографические (координатные) оси для семи сингоний

Рис. 3.25 Плоскости. 111 (жирная линия, частично заштрихована), 231 (очерчена пунктиром; полностьюзаштрихована)и324 (очерченаточками)
ря тому, что все отрезки, отсекаемые гранями кристалла на осях, являются относительными и, если потребуется, могут быть легко выражены в размерах ребер элементарной ячейки, когда они определены рентгеновским методом. Расчет осевых отношений по значениям углов между гранями показан на рис. 3.30.
3.5.2 Миллеровские символы граней кристаллов
Миллеровская1 система индексов обеспечивает простой принцип обозначения для описания наклонов граней кристалла на основе измерения единиц длины. Сначала записывают длину отсекаемых гранью отрезков в значениях единиц измерения a, b и c. На рис. 3.25 для параметрической
плоскости, очерченной жирной линией, они будут равны
1a 1b 1c,
а для других показанных плоскостей
1/2a 1/3b 1c 4/Зa 2b 1c
Поскольку отрезки всегда записываются в порядке а, 6, с, то сами эти буквы можно опускать. Затем берем обратные величины длины отсекаемых отрезков и преобразуем их до целых чисел. Получаем
|
|
|
Отрезки |
Обратные |
Миллеровские |
величины |
индексы |
|
|
|
|
111 |
1/1 1/1 1/1 |
111 |
1/2 1/3 1 |
2/1 3/1 1/1 |
231 |
4/32 1 |
3/4 1/2 1/1 |
324 |
|
|
|
Три индекса Миллера, взятые вместе, составляют миллеровский символ грани и определяют ее относительный наклон.
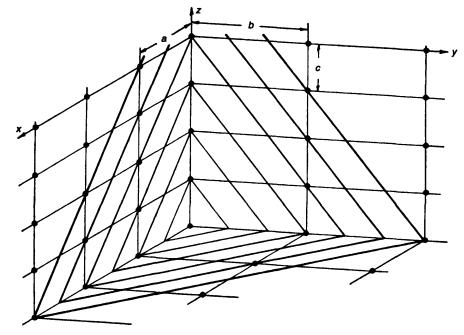
Рис. 3.26 Семейство плоскостей 231
Если какой-либо отрезок находится на отрицательном конце оси, то он обозначается черточкой над цифрой индекса, например 321, и произносится: три, два с чертой, один. Если в индексах появляется двузначное число, то числа разделяются точками, например: 11.1.6.
Грани, параллельные оси, пересекаются с ней в бесконечности. Поэтому, к примеру, для куба (рис. 3.32) имеем
|
|
|
|
Обратные |
Миллеровские |
Отрезки |
величины |
индексы |
|
|
|
1,οο,οο |
1/1,1/оо,1/оо |
100 |
|
|
|
На рис. 3.26 показана часть семейства плоскостей с отрезками 1/2a, 1/Зb, 1c и миллеровским символом 231. Плоскости с таким наклоном были построены с использованием в качестве исходных точек последовательного ряда узлов решетки. (На рисунке показаны узлы, которые в кристаллографически параллельных плоскостях являются эквивалентными и имеют один и тот же символ.) Заметим, что последовательные плоскости разделяют длины a, b и c на ряд частей, равных цифре индекса для этой оси. Другой способ определения
индексов состоит в следующем. Если отрезки всегда выражаются как дробные части единицы измерения с числителем, равным 1, то знаменатели непосредственно представляют собой индексы Сказанное позволяет сформулировать общее правило:
Если семейство плоскостей рассекает стороны ячейки a, b и c на части h, k и l соответственно, то образующиеся отрезки будут a/h, b/k и c/l, а индексы hkl.
В кристаллографии символ hkI широко используется для обозначения «любой плоскости» в общем смысле.
Говоря о числах миллеровских индексов, следует отметить четыре момента.
1. Поскольку параллельные плоскости эквивалентны друг другу, цифры в символе всегда сокращаются до их наименьших значений. Например, в описании внешней морфологии кристаллов символ 022 не встречается, будучи эквивалентным 011. Однако при изучении структуры кристаллов дифракционными методами символ 022 и подобные ему имеют смысл. Как видно из рис. 3.27, может существовать семейство плоскостей, которые следует обозначать именно так. Они, хотя и па-
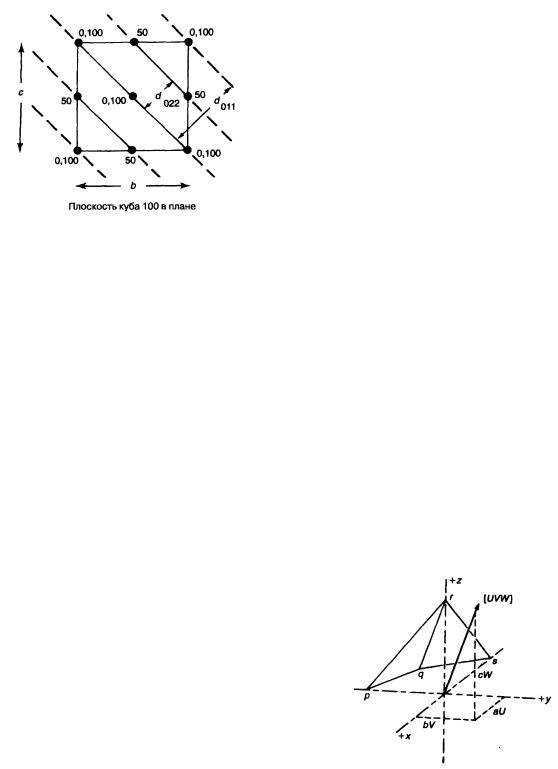
Рис. 3.27 Различие в пространственном расположении плоскостей, обозначенных 011 и 022.
раллельны 011, имеют меньшее межплоскостное расстояние d, чем семейство 011. Поэтому характеристика конкретного семейства плоскостей, которая теряется в случае изучения только углов между гранями, становится значимой, когда рентгеновскимиметодамиизмеряютсямежплоскостные расстояния.
2. Благодаря введению обратных величин при определении миллеровских индексов, относительно большая цифра индекса обозначает сравнительно небольшой отрезок на оси, к которой он относится. Отсюда следует правило — чем больше число, тем меньше отрезок.
3. Система обозначений. Символ 110 обозначает ряд плоскостей данного наклона (и пространственного расположения). Символ (110) строго соответствует обозначению единичной грани, правда скобки часто опускают. Символом {110} обозначают все грани какой-либо одной формы (разд.
3.6.1).
4. В гексагональной и тригональной сингониях имеется четыре (а не три) кристаллографические оси, а потому миллеровский индекс в этих системах состоит не из трех, а из четырех цифр. Добавочные индексы обозначают символом г (в целом hkil). Однако из-за особенностей взаимоотношений между осями ж, у и и в плоскости, перпендикулярной тройной или шестерной оси, индексы hki всегда подчиняются уравнению h + k = -i. Поэтому индекс г часто опускают и заменяют точкой (hk.l).
3.5.3 Символ зоны
Определенные соотношения существуют между миллеровскими символами граней и символами для осей зоны. Зоной называется совокупность граней с параллельными ребрами, а общее направление ребер именуют осью зоны (рис. 3.28). Ось зоны можно обозначить координатами U, V, W, которые представляют собой множители при отрезках ячейки, отсекаемых на кристаллографических осях координат. На рис. 3.28 жирной линией показана ось зоны, параллельная направлению ребра qr, по которому пересекаются грани pqr и qrs. Символ зоны [UVW] заключен в квадратные скобки, чтобы показать, что он относится к линии, а не к плоскости. Рассмотрение подобных взаимоотношений не входит в задачи данной книги, но их описание можно найти в работах по кристаллографии (см. рекомендации для дальнейшего чтения в конце главы). Здесь же мы удовлетворимся упоминанием только двух из них.
1. Правило сложения (частный случай закона зоны Вейса) утверждает, что если сложить индексы двух граней одной зоны, то они всегда сведутся к индексам грани, лежащей между ними и являющейся наклонной к находящемуся между ними ребру. Данное правило зачастую позволяет при внимательном просмотре индексировать грани на стереограмме, когда основным граням индексы уже присвоены. Это оказывается особенно полезным, если грань, которую нужно индексировать, лежит на пересечении двух зон. Подобные примеры можно видеть на рис. 3.29.
Рис. 3.28 Символ зоны.
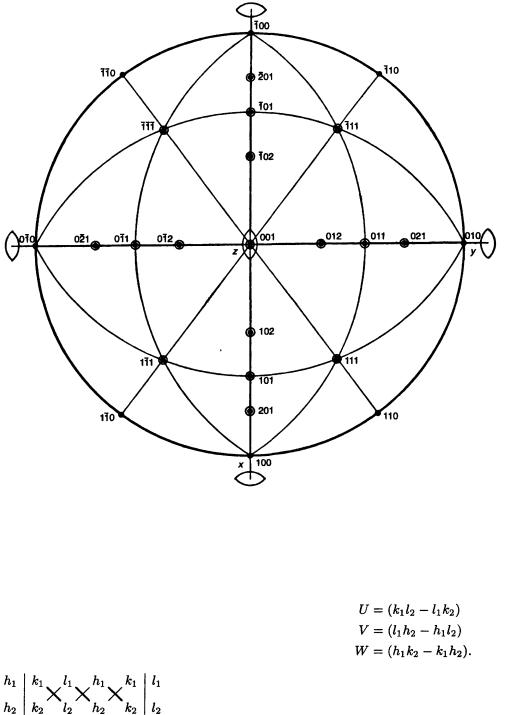
Рис. 3.29 Стереограмма, иллюстрирующая правило сложения для индексов одной и той же зоны.
2. Чтобы проверить, лежит ли третья грань в одной зоне с двумя другими, мы находим символ зоны двух граней, определяя зону таким способом: пишем индексы каждой грани два раза, располагая индексы второй грани под индексами первой; затем отсекаем конечные члены каждого ряда следующим образом:
В каждой группе, связанной крестом, перемножаем числа, соединенные жирной линией, и вычитаем из полученного результата произведения
пар, соединенных тонкими линиями, производя эту операцию слева направо. В итоге получаем символ зоны
Сделайте то же самое с индексами одной из этих двух граней и индексами третьей грани. Если третья грань находится в одной зоне с этими двумя, то символ зоны должен быть тем же, что прежде.
Например, из рис. 3.46 следует, что грань 5161 находится в одной зоне с 0111 и 1121. При этом в
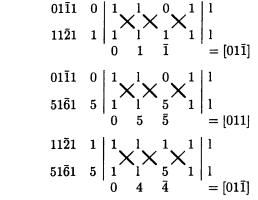
гексагональнойитригональнойсистемах мыопускаем третью цифру в описании индекса, так как онаненужнадляописанияплоскостей. Тогдаимеем
или
В каждом случае символ зоны одинаков, и, следовательно, эти три грани лежат в одной зоне.
3.5.4 Расчетосевыхотношений
Обратимся к рис. 3.15, на котором в демонстрационных целях была приведена кристаллическая решетка с заданными нами размерами ячейки, и нанесем полюса ее основных граней на стереограмму для установления симметрии решетки. Результат такой операции показан на рис. 3.29.
В ромбической системе в качестве кристаллографических осей берутся двойные оси симметрии. Они определяют только одну плоскость, которая пересекает оси x, у и z и поэтому принимается за единичную грань1 с обозначением 111. Грани, перпендикулярные к трем двойным осям, получают обозначения 100, 010 и 001.
Все грани в зоне между 001 и 100 будут перпендикулярны к плоскости xz и параллельны у, поэтому их второй индекс 0. Аналогичным образом все полюса на плоскости уz имеют в индексе О на первом месте, тогда как грани основного круга, будучи параллельны z, содержат 0 на последнем месте. Плоскости, представленные полюсами, расположенными в зоне 001-111, будут иметь такие же отношения отрезков, отсекаемых на осях
x и у, как и единичная грань, и, следовательно, обладать индексами, у которых первые два числа одинаковы, например 110, 221 и т.д.
В зоне 100, 111, 111, 100 грань, пересекающая ребро между 111 и 111, будет иметь индексы, которые представляют собой сумму индексов этих двух граней, т.е. 022 = 011.
Когда индексирование достигло этой стадии, мы можем рассчитать отношения осей кристалла с помощью методов прямолинейной тригонометрии, используя углы между плоскостями, перпендикулярными кристаллографическим осям (плоскости с индексами 100, 010 или 001), и между теми плоскостями, которые пересекают две оси и параллельны третьей (101, 011, 110). Если искомая плоскость не выражена гранью кристалла, то ее положение может быть определено по стереограмме путем построения больших кругов, отображающих две зоны, в которых она может находиться. Точка пересечения этих кругов устанавливает место нахождения искомого полюса. Теперь по стереограмме можно измерить (приблизительно) угол между плоскостями.
На рис. 3.30 показаны тригонометрические соотношения, использованные при расчете осевых отношений для нескольких кристаллографических систем (исключая триклинную). Осевые отношения в триклинной системе лучше всего рассчитывать векторными методами, так как использование тригонометрического подхода для нее оказывается сложным. Подобные расчеты на стереограмме рис. 3.29 для кристаллов ромбической симметрии приведут нас снова к осевому отношению
a: b: c = 0,75: 1 : 1,5,
исходя из которого были первоначально получены углы между гранями на рис. 3.15 и в сопровождающей его табл. 3.2.
Осевые отношения можно также вычислить путем решения сферических треугольников в стереографической проекции. Мы не будем здесь касаться этого метода, так как с помощью современных компьютеров такие расчеты легче выполняются векторными методами. Для освоения сферической тригонометрии мы отошлем читателя к старым кристаллографическим руководствам, например к книге F. С. Phillips, An introduction to crystallography, 4th ed., London, Longman, 1977.
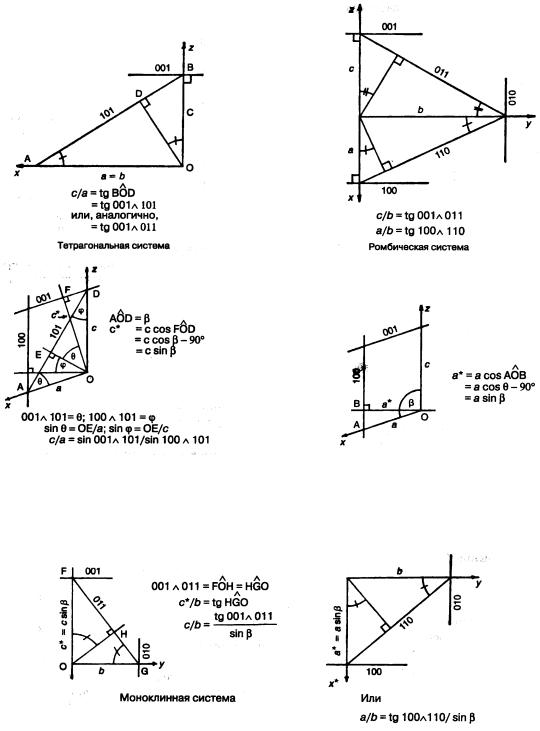
Рис. 3.30 Расчет осевых отношений.
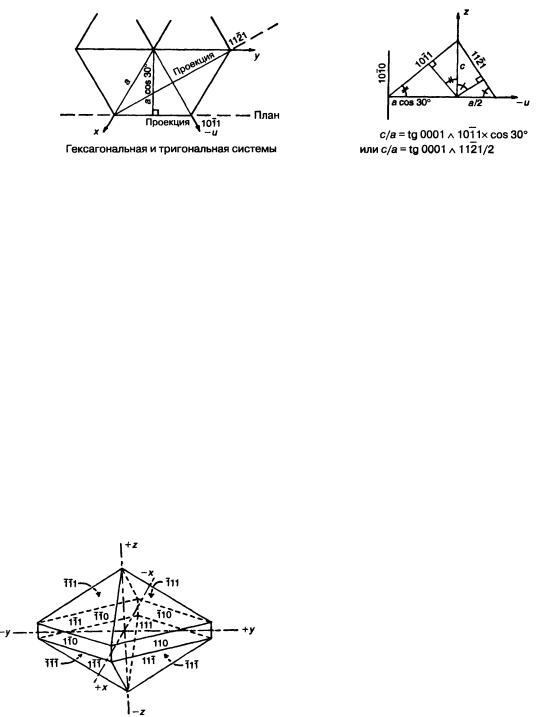
Рис. 3.30 Продолжение
3.6 Простые формы кристаллов
На рис. 3 31 обозначены все грани простой формы {111} циркона. Эти плоскости 111, 111, 111, 111, 111, 111, 111, 111 образуются за счет операции элементов тетрагональной симметрии на единичном полюсе стереограммы. Все они имеют одинаковый наклон относительно кристаллографических осей, хотя и направленный в разные стороны. Вместе они образуют простую форму {111}, обозначенную взятым в фигурные скобки миллеровским символом для грани, которая пересекает всеоси в их положительных направлениях. На рисунке также обозначены все грани простой формы {110}
Рис 3.31 Грани простых форм {111} и {110} в кристалле циркона
3.6.1Наименования простых форм кристаллов
Впроцессе своего развития кристаллография обросла изобилием терминов. Так, некоторые главные сингонии называются по-разному, а клас-
сы имеют по три-четыре наименования, используемых разными авторами. В свою очередь, наблюдается дублирование и в названиях простых форм в каждом классе. Некоторые наименования широко используются, но большинство их употребляется редко, так как не несет большей информации, чем миллеровские символы простых форм. Однако имеется ряд важных исключений, которые рассматриваются ниже.
Уникальные, частные и общие простые формы
Этими терминами описываются соотношения граней и элементов симметрии. Уникальная форма образуется из плоскости, перпендикулярной оси симметрии Такая плоскость, будучи перпендикулярной к линии, обладающей определенным направлением по отношению к кристаллографическим координатным осям, может сама иметь только один наклон относительно этих осей. Следовательно, по отношению к этим осям она получает уникальный миллеровский символ (всегда с одними и теми же цифрами, но, конечно, с разным порядком их написания) Примером такой простой формы является куб (рис. 3.32), плоскость которого с символом 100 (или 100, 010 и т.д.) перпендикулярна четверной оси в кубической системе.
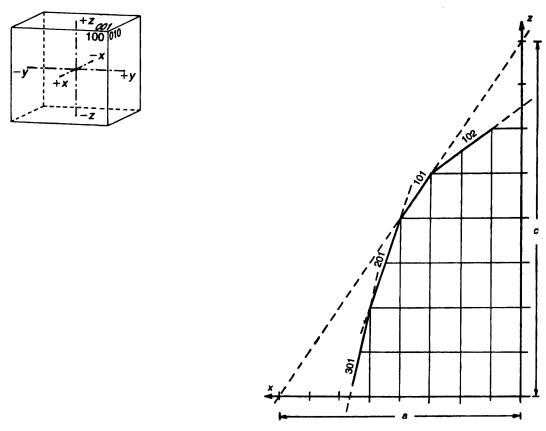
Рис. 3.32 Куб как пример уникальной простой формы.
Наклоны грани, перпендикулярной к плоскости симметрии, могут изменяться по отношению к кристаллографическим осям. Однако существует ограничение, согласно которому эта грань всегда должна быть перпендикулярна плоскости, которая, в свою очередь, зафиксирована по отношению к осям. Таким образом, набор цифр в миллеровском символе всегда будет одинаковым. Такая форма называется частной формой из-за ее особого взаимоотношения с элементами симметрии. В качестве примера на рис. 3.33 показаны проекции плоскостей для семейства простых форм в ромбической системе, которые все перпендикулярны плоскости симметрии, содержащей кристаллографические оси x иz. Отметим, что возможный для них набор символов в обобщенном виде может быть представлен как h0l, где h и l — любые целые числа, а 0 встречается во всех случаях, что свидетельствует о параллельности всех элементов оси у. На рис. 3.24 показана в стереографическом изображении форма 211, перпендикулярная диагональным плоскостям симметрии кубической сингонии. Образующееся геометрическое тело представляет собой тетрагонтриоктаэдр (рис. 3.34). При этом наблюдается семейство плоскостей, обозначаемых 311, 322 и т.д., символ которых в общем виде имеет вид hll, где h > l.
Грань, которая не находится в особом положении по отношению к какому-либо элементу симметрии, может иметь в качестве миллеровского символа любую комбинацию цифр, хотя, как мы видели, простые формы с большими числами для индексов в символе встречаются редко, так как их плоскости обладают низкой плотностью атомов. Такая форма, имея символ типа hkl, назы-
Рис. 3.33 Семейство форм h0l, связанных с плоскостью xz.
вается общей простой формой. Когда полюс грани, находящейся в такой общей позиции по отношению к элементам симметрии, наносится на стереограмму, он будет повторяться за счет проявления симметрии и давать максимально возможное число граней любой простой формы в этом классе кристаллов. Изучение общей простой формы неизвестного кристалла позволяет выявлять имеющуюся полную симметрию, тогда как в голоэдрических классах кристаллографических систем (табл. 3.1) и в классах с более низкой симметрией могут присутствовать частные или уникальные формы с точно такими же внешними проявлениями. Так, пирит представлен обычными кубами, хотя мы видели раньше, что он обладает меньшей симметрией, чем полная кубическая.
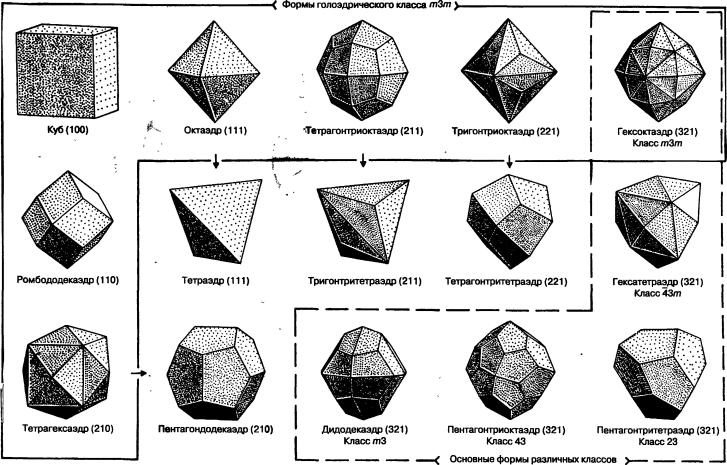
Рис. 3.34 Простые формы кубической сингонии.
