1 Магнитное поле. Магнитная индукция. Линии магнитной индукции. Графическое изображение магнитных полей. Поток вектора магнитной индукции. Теорема Остроцкого – Гаусса.

Магнитное поле — составляющая электромагнитного поля, появляющаяся при наличии изменяющегося во времени электрического поля. Кроме того, магнитное поле может создаваться током заряженных частиц, либо магнитными моментами электронов в атомах (постоянные магниты).

Магни́тная инду́кция —векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Показывает, с какой силой магнитное поле действует назаряд , движущийся со скоростью.

Линиями магнитной индукции (силовыми линиями магнитного поля) называются линии, проведенные в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с направлением вектора В в этой точке поля.

Линии магнитной индукции проще всего наблюдать с помощью мелких

Игольчатых железных опилок, которые намагничиваются в исследуемом поле и ведут себя подобно маленьким магнитным стрелкам (свободная магнитная стрелка разворачивается в магнитном поле так, чтобы ось стрелки, соединяющая ее южный полюс с северным, совпадала с направлением В).

Вид линий магнитной индукции простейших магнитных полей показан

на рис. Из рис. б — г видно, что эти линии охватывают проводник с током, создающий поле. Вблизи проводника они лежат в плоскостях, перпендикулярных проводнику.

Н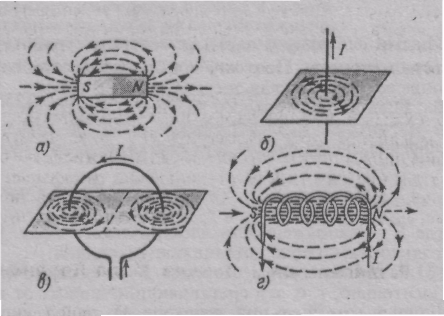аправление линий индукции определяется поправилу буравчика: если ввинчивать буравчик по направлению вектора плотности тока в проводнике, то направление движения рукоятки буравчика укажет направление линий магнитной индукции.

Линии индукции магнитного по­ля

тока ни в каких точках не могут обрываться, т. е. ни начинаться, ни кончаться: они либо замкнуты (рис. б, в, г), либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя ее, но никогда не возвращаясь вторично в любую точку поверхности.

Теорема Гаусса для магнитной индукции

Поток вектора магнитной индукциичерез любую замкнутую поверхность равен нулю:

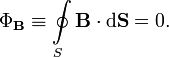Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле являетсявихревым.

2 Закон Био- Савара – Лапласа

Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме,— точка, в которой ищется поле, тогдаиндукциямагнитного поля в этой точке выражается интегралом (в системеСИ)

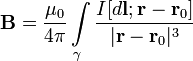
Направление перпендикулярнои, то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линиимагнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление, если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектораопределяется выражением (в системеСИ)

Векторный потенциалдаётся интегралом (в системеСИ)

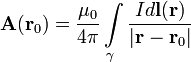
Закон Био — Савара — Лапласа может быть получен из уравнений Максвелладля стационарного поля. При этом производные по времени равны 0, так что уравнения для поля в вакууме примут вид (в системеСГС)

где —плотность токав пространстве. При этом электрическое и магнитное поля оказываются независимыми. Воспользуемся векторным потенциалом для магнитного поля (в системеСГС):

Калибровочная инвариантностьуравнений позволяет наложить на векторный потенциал одно дополнительное условие:

Раскрывая двойной роторпоформуле векторного анализа, получим для векторного потенциала уравнение типауравнения Пуассона:

Его частное решение даётся интегралом, аналогичным ньютонову потенциалу:

Тогда магнитное поле определяется интегралом (в системе СГС)

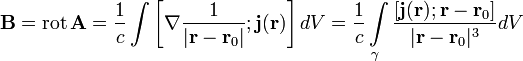
аналогичным по форме закону Био — Савара — Лапласа. Это соответствие можно сделать точным, если воспользоваться обобщёнными функциямии записать пространственную плотность тока, соответствующую витку с током в пустом пространстве.Переходяот интегрирования по всему пространству к повторному интегралу вдоль витка и по ортогональным ему плоскостям и учитывая, что

получим закон Био — Савара — Лапласа для поля витка с током.