3.3. Задача о росте дерева [1, с. 66]

Свободную энергию (активные вещества) дерево получает путем фотосинтеза. Она расходуется на собственно сам процесс фотосинтеза, на рост дерева (то есть на построение живой ткани) и на подъем раствора питательных веществ из почвы. За большие промежутки времени растение получает постоянное количество света на единицу поверхности и может поглощать питательные вещества из неограниченного запаса. Найти закон роста дерева любой породы, учитывая, что зрелое растение в процессе роста сохраняет свои пропорции.

Пусть функция  x = x( t) описывает линейные размеры дерева в момент времени  t, используемые для высоты и вычисления площади поверхности зеленой части (кроны) дерева, а также объема растения.

Составим уравнение баланса энергии.

Свободная энергия  E_ф образуется путем фотосинтеза в зеленой части растения и ее величина растет пропорционально поверхности ее кроны, то есть

E_ф = k₁x­­²,

где  k₁ — коэффициент пропорциональности, зависящий от размеров и формы листвы, а также от интенсивности фотосинтеза.

Энергия от фотосинтеза  E_ф будет расходоваться полностью на следующие процессы:

1. Собственно процесс фотосинтеза, энергию на который аналогично вычисляем по формуле

E₁ = k₂x­­², ( k₂ < k₁).

2. Доставку питательных веществ во все части растения, энергия на которую пропорциональна объему растения и его высоте, так как подъем питательного раствора связан с преодолением силы тяжести. Таким образом

E₂ = k₃x­­³x­­ = k₃x­­⁴.

3. Рост растения и увеличение его массы пропорционально скорости изменения массы

m =  x­­³,

где   — средняя плотность растения, то есть

E₃ = k₄(x­­³) = 3 k₄x­­²x .

Согласно закону сохранения энергии

E_ф = E₁ + E₂ + E₃

или

k₁x­­² = k₂x­­² + k₃x­­⁴ + 3 k₄x­­²x .

Разделим данное уравнение на  3 k₄x­­² :

.

Обозначив

и ,

получим дифференциальное уравнение роста дерева:

x  = a² – b²x²,

и  x² < (a/b)² так как дерево растет, то есть производная от функции роста должна быть положительной.

Это уравнение с разделяющимися переменными. Представляя производную в виде , имеем

.

Интегрируя левую часть по  x, а правую — по переменной  t, получаем

.

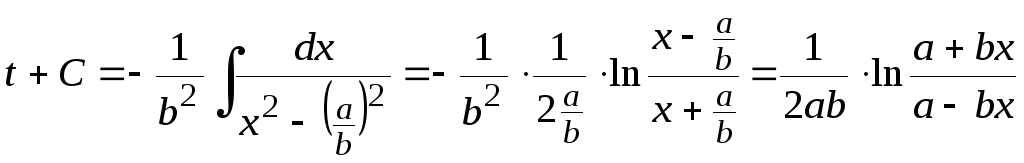В начальный момент времени  t = t₀ функция роста дерева  x = x( t₀) = 0, то есть в момент посадки полагаем массу и "рост" семечка равным нулю. Из этого условия несложно найти, что произвольная константа  C = – t₀, так как натуральный логарифм от единицы равен нулю.

Окончательно получаем формулу

,

из которой выводится закон роста дерева:

.

Так как для деревьев каждой породы константы  a и  b известны, то можно с помощью данной формулы вычислить средний рост дерева данной породы в зависимости от его возраста, то есть от времени  t. Исследуем этот закон при изменении времени.

Дифференцируя уравнение роста дерева по t еще раз, получим

x  = – 2 b²xx .

Но  x > 0 как рост дерева, а производная первого порядка положительна ввиду того, что дерево растет. То есть правая часть данного равенства отрицательна. Это значит, что закон роста является возрастающей выпуклой вверх функцией.

Переписав закон роста в виде

легко заметить, что рост ограничен числом и

.

П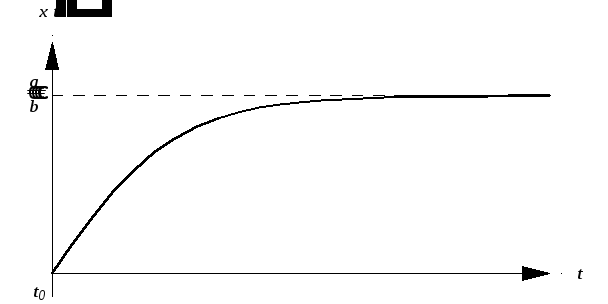оэтому график функции роста будет иметь следующий вид:

Рис. 3.2

Предельное положение соответствует случаю нулевой скорости роста, то есть вся энергия, поступающая от фотосинтеза, расходуется лишь на поддержание жизнедеятельности растения.

Решение данной задачи вполне достоверно объясняет причины остановки роста у деревьев различных пород по достижении определенного возраста, то есть роста, веса, объема кроны и т.п.

Пример. Известно, что средняя максимальная высота дерева исследуемой породы равна 12 метров, а в возрасте 20 лет его средняя высота равна 10 метрам.

Тогда , как предельное значение закона роста, а произведениеab найдем из второго условия, подставив числовые данные в уравнение:

.

Отсюда находим, что . Таким образом, закон примет вид:

,

где t₀ — год посадки дерева, а t — текущий год.