Задача 6-2

Варіант №7

На підставі даних про продуктивність праці робітника Y=(42; 51; 57; 47; 37) за певну годину Х=(1; 2; 4; 5; 6) знайти залежність між змінними Y та X за методом найменших квадратів. Визначити обсяг продукції, яка буде вироблена за 8 годин роботи безпосереднім інтегруванням функції у(х) та за допомогою наближеного обчислення цього визначеного інтеграла за формулами прямокутників, трапецій і Сімпсона.

Вихідні дані:

Хі	1	2	4	5	6
Уі	42	51	57	47	37

Розв’язання:

Запишемо таку систему рівнянь:

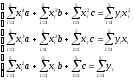
Побудуємо розрахункову таблицю для вирішення задачі:

№	Xi	Yi	X2	X3	X4	X·Y	X2·Y
1	1	42	1	1	1	42	42
2	2	51	4	8	16	102	204
3	4	57	16	64	256	228	912
4	5	47	25	125	625	235	1175
5	6	37	36	216	1296	222	1332
Σ	18	234	82	414	2194	829	3665

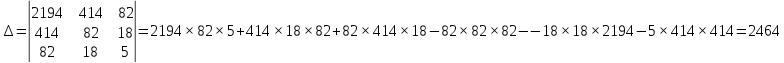
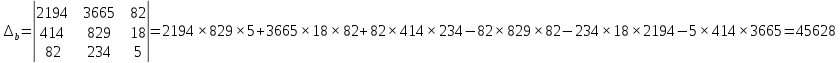
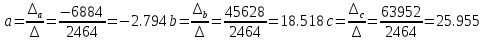
Отже рівняння матиме вигляд:

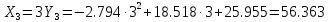
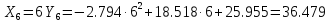
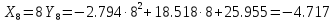
n=8, a=0, b=8

Формула лівих прямокутників:

Формула правих прямокутників:

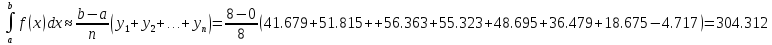
Формула трапецій:

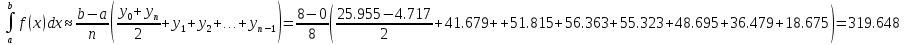
Формула Сімпсона:

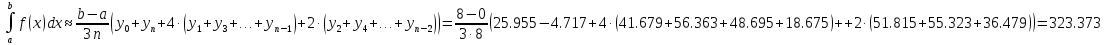
Отже, можна зробити висновки, що формула Сімпсона виявилась найточнішою.

3