Задача № 7

Показатель наглядности представляет собой процентное отношение какого-либо показателя в динамическом ряду к исходному уровню, принятому за 100 %.

Таким образом, принимаем показатель заболеваемости с ВУТ в 1996 году за 100% (исходный уровень.

Для расчета показателя наглядности за 1997 год строим пропорцию:

180 случаев заболеваний с ВУТ в 1996 году – 100%

160 случаев заболеваний с ВУТ в 1997 году – Х.

Решаем пропорцию:

Для расчета показателя наглядности за 1998 год строим пропорцию:

180 случаев заболеваний с ВУТ в 1996 году – 100%

150 случаев заболеваний с ВУТ в 1998 году – Х.

Решаем пропорцию:

Для расчета показателя наглядности за 1999 год строим пропорцию:

180 случаев заболеваний с ВУТ в 1996 году – 100%

140 случаев заболеваний с ВУТ в 1999 году – Х.

Решаем пропорцию:

Для расчета показателя наглядности за 2000 год строим пропорцию:

180 случаев заболеваний с ВУТ в 1996 году – 100%

130 случаев заболеваний с ВУТ в 2000 году – Х.

Решаем пропорцию:

Для расчета показателя наглядности за 2001 год строим пропорцию:

180 случаев заболеваний с ВУТ в 1996 году – 100%

120 случаев заболеваний с ВУТ в 2001 году – Х.

Решаем пропорцию:

Для расчета показателя наглядности за 2002 год строим пропорцию:

180 случаев заболеваний с ВУТ в 1996 году – 100%

110 случаев заболеваний с ВУТ в 2002 году – Х.

Решаем пропорцию:

Таким образом, преобразованная таблица условия задачи будет выглядеть следующим образом.

Годы	1996	1997	1998	1999	2000	2001	2002
Наглядные показатели заболеваемости с ВУТ, %	100	88,89	83,33	77,78	72,22	66,67	61,11

Далее, строим столбиковую и линейную диаграммы, отражающие рассчитанный показатель наглядности. На столбиковой диаграмме находим тренд, демонстрирующий устойчивость тенденции, и оцениваем его.

Рисунок Х – Динамика заболеваемости с временной утратой трудоспособности на промышленном предприятии, число случаев на 100 работающих (вариант 1)

Рисунок Х – Динамика заболеваемости с временной утратой трудоспособности на промышленном предприятии, число случаев на 100 работающих (вариант 2)

Значение R²(тренда) свидетельствует о выраженной устойчивой тенденции в динамике заболеваемости с ВУТ.

Задача № 8

Строим заданные диаграммы и анализируем их.

Рисунок Х – Динамики показателей естественного прироста населения в г. Nк 1913 году в процентах (вариант 1)

Рисунок Х – Динамики показателей естественного прироста населения в г. Nк 1913 году в процентах (вариант 2)

Значение R²(тренда) свидетельствует о выраженной устойчивой тенденции в динамике естественного прироста.

Задача № 9

Вычисление групповых средних.

Данную задачу можно решить, выделив из представленного динамического ряда 3 группы: 1 группа – 1989, 1990, 1991, 1992 годы; 2 группа – 1993, 1994, 1995, 1996 годы; 3 группа – 1997, 1998, 1999, 2000 годы.

Для вычисления групповых средних суммируем показатели числа родившихся по группам и делим результат на число лет в каждой указанной выше группе.

По 1 группе:

По 2 группе:

По 3 группе:

Преобразованный динамический ряд, представленный в виде таблицы, будет, таким образом, выглядеть следующим образом,

Годы	В 1989-1992 годах	В 1993-1996 годах	В 1997-2000 годах
Среднее число родившихся за каждый год	1148	1166	1158

Вычисление скользящей средней.

Данную задачу можно решить, выделив из представленного динамического ряда 6 групп: 1 группа – 1989, 1990; 2 группа – 1991, 1992 годы; 3 группа - 1993, 1994; 4 группа - 1995, 1996; 5 группа – 1997, 1998; 6 группа - 1999, 2000 годы.

Для вычисления скользящих средних суммируем показатели числа родившихся по группам и делим результат на число лет в каждой указанной выше группе (2).

По 1 группе:

По 2 группе:

По 3 группе:

По 4 группе:

По 5 группе:

По 6 группе:

Преобразованный динамический ряд, представленный в виде таблицы, будет, таким образом, выглядеть следующим образом,

Годы	1989-1990	1991-1992	1993-1994	1995-1996	1997-1998	1999-2000
Среднее число родившихся за каждый год	1130	1167	1167	1165	1164	1151

Вычисляем показатели абсолютного прироста - разности последующего и предыдущего уровней в абсолютных величинах.

Для 1990 года: 1150 – 1110 = 40

Для 1991 года: 1165 – 1150 = 15

Для 1992 года: 1169 – 1165 = 4

Для 1993 года: 1170 – 1169 = 1

Для 1994 года: 1165 – 1170 = -5

Для 1995 года: 1150 – 1165 = -15

Для 1996 года: 1180 – 1150 = 30

Для 1997 года: 1175 – 1180 = -5

Для 1998 года: 1154 – 1175 = -21

Для 1999 года: 1153 – 1154 = -1

Для 2000 года: 1150 – 1153 = -3

Представляем показатели абсолютного прироста в виде таблицы.

Годы	1990	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000
Показатель абсолютного прироста	40	15	4	1	-5	-15	30	-5	-21	-1	-3

Строи диаграммы.

Рисунок Х – Динамика абсолютного прироста числа родившихся на 1000 человек в г. N(вариант 1)

Рисунок Х – Динамика абсолютного прироста числа родившихся на 1000 человек в г. N(вариант 2)

Значение R²(тренда) свидетельствует о неустойчивой тенденции в динамике рождаемости населенном пунктеN.

Вычисляем темп прироста - процентное отношение абсолютного прироста к предыдущему уровню.

Составляем пропорции и решаем их; при этом используем результаты расчетов абсолютного прироста.

Для 1990 года:

1110 – 100%

40 – Х

Для 1991 года:

1150 – 100%

15 – Х

Для 1992 года:

1165 – 100%

4 – Х

Для 1993 года:

1169 – 100%

1 – Х

Для 1994 года:

1170 – 100%

-5 – Х

Для 1995 года:

1165 – 100%

-15 – Х

Для 1996года:

1150 - 100%

30 – Х

Для 1997года:

1180 - 100%

-5 – Х

Для 1998 года:

1175 - 100%

-21 – Х

Для 1999 года:

1154 - 100%

-1 – Х

Для 2000 года:

1153 - 100%

-3 – Х

Представляем показатели темпа прироста в виде таблицы.

Годы	1990	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000
Показатель темпа прироста, %	3,60	1,30	0,34	0,08	-0,43	-1,29	2,61	-0,42	-1,79	-0,09	-0,26

Рисунок Х – Темп прироста числа родившихся на 1000 человек в г. Nв процентах (вариант 1)

Рисунок Х – Темп прироста числа родившихся на 1000 человек в г. Nв процентах (вариант 2)

Значение R²(тренда) свидетельствует о неустойчивой тенденции в динамике рождаемости населенном пунктеN.

Вычисляем темп роста - процентное отношение последующего уровня к предыдущему.

Составляем пропорции и решаем их.

Для 1990 года:

1110 – 100%

1150 – Х

Для 1991 года:

1150 – 100%

1165 – Х

Для 1992 года:

1165 – 100%

1169 – Х

Для 1993 года:

1169 – 100%

1170 – Х

Для 1994 года:

1170 – 100%

1165 – Х

Для 1995 года:

1165 – 100%

1150 – Х

Для 1996 года:

1150 – 100%

1180 – Х

Для 1997 года:

1180 – 100%

1175 – Х

Для 1998 года:

1175 – 100%

1154 – Х

Для 1999 года:

1154 – 100%

1153 – Х

Для 2000 года:

1153 – 100%

1150 – Х

Представляем показатели темпа роста в виде таблицы.

Годы	1990	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000
Показатель темпа роста, %	103,60	101,30	100,34	100,09	99,57	98,71	102,61	99,58	98,21	99,91	99,74

Строим диаграммы.

Рисунок Х – Темп роста числа родившихся на 1000 человек в г. Nв процентах (вариант 1)

Рисунок Х – Темп роста числа родившихся на 1000 человек в г. Nв процентах (вариант 2)

Значение R²(тренда) свидетельствует о неустойчивой тенденции в динамике рождаемости населенном пунктеN.

Задача № 10

В условии задачи динамика заболеваемости с ВУТ представлена в виде показателя наглядности.

Строим диаграммы.

Рисунок Х – Динамика заболеваемости с временной утратой трудоспособности (ВУТ) на N-ом промышленном предприятии, % (вариант 1)

Рисунок Х – Динамика заболеваемости с временной утратой трудоспособности (ВУТ) на N-ом промышленном предприятии, % (вариант 2)

Рисунок Х – Динамика заболеваемости с временной утратой трудоспособности (ВУТ) на N-ом промышленном предприятии, % (вариант 3)

Рисунок Х – Динамика заболеваемости с временной утратой трудоспособности (ВУТ) на N-ом промышленном предприятии, % (вариант 4)

Значение R²(тренда) свидетельствует о выраженной устойчивой тенденции в динамике заболеваемости с ВУТ.

Задача № 11

При анализе показателей инструментального контроля уровней ЭМП использован интенсивный показатель.

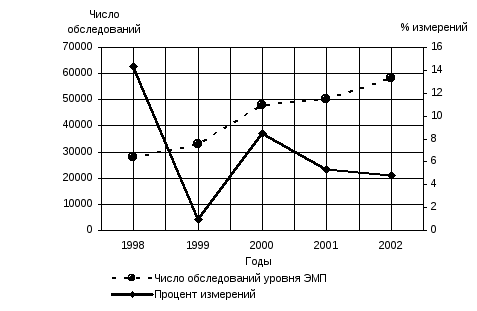
Рисунок Х – Показатели инструментального контроля за электромагнитными полями (ЭМП) в Российской Федерации в 1998-2002 годах (вариант 1)

Рисунок Х – Показатели инструментального контроля за электромагнитными полями (ЭМП) в Российской Федерации в 1998-2002 годах (вариант 2)

Значение R²(тренда) свидетельствует о выраженной устойчивой тенденции в динамике заболеваемости числа обследований и отсутствии тенденции или ее неясности при анализе тренда % измерений.

Задача № 12

Для анализа динамики смертности населения Российской Федерации за 1990-2000 годы в сравнении с 1990 годом использован показатель темпа прироста.

Строим диаграммы

1- все причины; 2 - болезни системы кровообращения; 3 - болезни органов дыхания; 4 - болезни органов пищеварения; 5 - травмы (все); 6 - злокачественные опухоли (в целом); 7 - злокачественные опухоли органов дыхания; 8 - травмы на транспорте

Рисунок Х – Показатели смертности населения Российской Федерации за 1990-2000 годы в процентах к 1990 году (вариант 1)

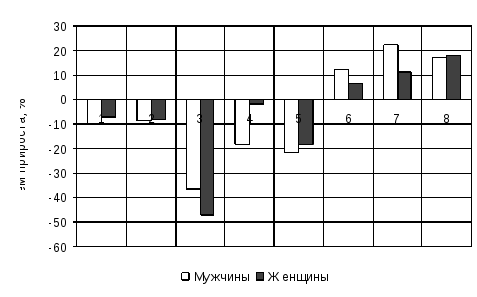
1- все причины; 2 - болезни системы кровообращения; 3 - болезни органов дыхания; 4 - болезни органов пищеварения; 5 - травмы (все); 6 - злокачественные опухоли (в целом); 7 - злокачественные опухоли органов дыхания; 8 - травмы на транспорте

Рисунок Х – Показатели смертности населения Российской Федерации за 1990-2000 годы в процентах к 1990 году (вариант 2)

Задача № 13

Группа А из 6000 людей участвовала в программе профилактики. Другая группа Б из 5000 человек не участвовала в программе и служила контрольной группой. Во время курса профилактики в течение года наблюдалось 36 случаев заболеваний в группе А и 35 случаев — в группе Б. Результаты даны в таблице, приведенной ниже, для двух возрастных категорий.

Подсчитайте частоты случаев в обеих популяция. Сделайте стандартизацию данных с эквивалентными весами для двух групп, а также проведите относительное сравнение стандартизованных частот (см. табл. «Группа А», «Группа Б»).

Решение. Возрастные частоты случаев:

	Группа А			Группа Б
молодые:	4	= 0,002		20	= 0,005
	2000			4000
старые:	32	= 0,008		15	= 0,015.
	4000			1000

Группа А

	Число человеко-дней	Число случаев
Молодых	2000	4
Старых	4000	32
Всего	6000	36

Группа Б

	Число человеко-дней	Число случаев
Молодых	4000	20
Старых	1000	15
Всего	5000	35

Стандартизованные по возрасту частоты (учитывая, что количество старых и пожилых людей одинаково, то есть их веса равны) вычисляются следующим образом:

Группа А:

где SIR — стандартизованный коэффициент заболеваемости, характеризующий величину относительного риска при сравнении двух популяций.

Задача № 14

В исследовании мужчины-рабочие, участвующие в процессе вулканизации, сравнивались со всеми работающими мужчинами в отношении случаев рака пищевода. Результаты приведены в таблице ниже.

Необходимо провести «косвенную» стандартизацию по возрасту и рассчитать SMR (см. табл. «Рабочие-вулканизаторы» и «Контрольная группа»).

Решение. Наблюдаемое число = 8.

Ожидаемое —

Как видно из расчетов, наблюдаемое число случаев в 10 раз превосходит ожидаемое. Стандартизованный коэффициент заболеваемости получится путем деления этих величин друг на друга. Часто он выражается в процентах:

SIR = 8/0,8  100% = 1000 %.

Рабочие-вулканизаторы

Возраст	Число с болезнью	Число мужчин
15-24	?	651
25-34	?	518
35-44	?	500
45-54	7	465
55-64	7	211
Всего	8	2345

Контрольная группа

Возраст	Число с болезнью	Число мужчин
15-24	0	337
25-34	6	431
35-44	90	522
45-54	381	507
55-64	626	367
Всего	1103	2164

Задача № 15

Из микрорайонов 2-х местных клиник были взяты случайные выборки из мужского населения в возрасте 30-69 лет. Исследовалась частота возникновения хронического бронхита на основе проведенного опроса о наличии симптомов данного заболевания. Результаты показаны в нижеследующих таблицах.

Требуется провести стандартизованное сравнение двух популяций, считая, что количество людей в возрастных группах одинаково, т. е. их веса равны.

Популяция 1

Возраст	Число людей в выборке	Число хронических бронхитов
30-39	1000	5
40-49	2000	20
50-59	4000	50
60-69	3000	50
Всего	10000	125

Популяция 2

Возраст	Число людей в выборке	Число хронических бронхитов
30-39	5000	25
40-49	3000	40
50-59	1000	20
60-69	1000	20
Всего	10000	105

Решение. Стандартизованная по возрасту распространенность (с равными весами):

где SIR — стандартизованный коэффициент заболеваемости, характеризующий величину относительного риска при сравнении двух популяций.

Задача № 16

Строим столбиковые диаграммы отдельно для мужчин и женщин, так как если отобразить материал таблицы на одной диаграмме, то она будет перегружена.

Рисунок Х – Средняя продолжительность жизни мужчин ряда стран в 1970–1995 годах по данным ВОЗ

Рисунок Х – Средняя продолжительность жизни женщин ряда стран в 1970–1995 годах по данным ВОЗ

Преобразуем таблицу с целью как можно более наглядного представления динамики показателя у мужчин и женщин по годам

Страна	Мужчины						Женщины
	Годы						Годы
	1970	1975	1980	1985	1990	1995	1970	1975	1980	1985	1990	1995
Швеция	72,2	72,4	73,5	74,0	75,0	75,8	77,4	78,0	79,5	80,0	80,6	82,1
Франция	68,3	69,0	70,0	71,8	72,1	73,4	75,8	76,9	78,6	79,5	80,6	83,9
Германия	67,3	68,0	70,0	71,8	72,1	73,2	73,7	74,7	76,8	78,0	79,1	81,8
Россия	63,5	63,0	62,1	63,5	62,0	57,2	73,7	73,5	73,1	73,5	74,2	71,0

Задача № 17

Строим круговые диаграммы.

В целом плавсостав ДВМП	Капитаны
Механики	Мотористы
Матросы	Обслуживающий персонал

Рисунок Х – Распределение профессиональных групп плавсостава ДВМП по уровню массы тела (МТ) в процентах (вариант 1)

Рисунок Х – Распределение профессиональных групп плавсостава ДВМП по уровню массы тела (МТ) в процентах (вариант 2)

На показатели массы тела в значительной степени оказывает влияние фактор подвижности, так как процент представителей профессиональных групп с меньшей подвижностью (капитаны, механики) значительно превышает показатель в группах с более высокими энергетическими затратами (мотористы, матросы).

Задача № 18

Для решения задачи строим рабочую таблицу, преобразуя вариационные ряды с тем, чтобы показатели располагались для удобства расчетов по возрастающей.

Процент работников предприятий общественного питания, в смывах кистей рук которых обнаружена E. Coli, до и после проведения профилактических мероприятий (V)		Отклонения от средней (d = V - M)		Квадраты отклонений от средней (d2)
V1	V2	d1	d2
2,6	1,3	-3,27	-3,38	10,6929	11,4244
2,8	2,6	-3,07	-2,08	9,4249	4,3264
3,7	3,6	-2,17	-1,08	4,7089	1,1664
4,2	3,9	-1,67	-0,78	2,7879	0,6084
4,4	4,0	-1,47	-0,68	2,1609	0,4624
4,7	4,1	-1,17	-0,58	1,3689	0,3364
5,0	4,2	-0,87	-0,48	0,7569	0,2304
5,1	4,4	-0,77	-0,28	0,5929	0,0784
5,1	4,6	-0,77	-0,08	0,5929	0,0784
5,3	4,8	-0,57	+0,12	0,3249	0,0144
6,2	4,8	+0,33	+0,12	0,1089	0,0144
6,4	4,9	+0,53	+0,22	0,2809	0,0484
8,3	5,1	+2,43	+0,42	5,9049	0,1764
8,4	5,6	+2,53	+0,92	6,4009	0,8464
8,5	6,5	+2,63	+1,82	6,9169	3,3124
9,3	7,4	+3,43	+2,72	11,7649	7,3984
9,8	7,7	+3,93	+3,02	15,4449	9,1204
ΣV1 = 99,8	ΣV2 = 79,5			= 80,2343 ≈ 80,23	= 39,6428 ≈ 39,64

1 этап.Вычисляем суммы показателей в обоих вариационных рядах и заносим результаты в соответствующие колонки таблицы.

2 этап. Из средних величин выбираем среднюю арифметическую (М). Рассчитываем М для каждого из двух вариационных рядов (М₁и М₂).

3 этап.По каждой варианте каждого вариационного ряда рассчитываем разность между значением варианты и средней арифметической.

Для первого вариационного ряда:

dдля 1-ой варианты = 2,6 – 5,87 = -3,27;

dдля 2-ой варианты = 2,8 – 5,87 = -3,07;

dдля 2-ей варианты = 3,7 – 5,87 = -2,17;

dдля 4-ой варианты = 4,2 – 5,87 = -1,67;

dдля 5-ой варианты = 4,4 – 5,87 = -1,47;

dдля 6-ой варианты = 4,7 – 5,87 = -1,17;

dдля 7-ой варианты = 5,0 – 5,87 = -0,87;

dдля 8-ой варианты = 5,1 – 5,87 = -0,77;

dдля 9-ой варианты = 5,1 – 5,87 = -0,77;

dдля 10-ой варианты = 5,3 – 5,87 = -0,57;

dдля 11-ой варианты = 6,2 – 5,87 = +0,33;

dдля 12-ой варианты = 6,4 – 5,87 = +0,53;

dдля 13-ой варианты = 8,3 – 5,87 = +2,43;

dдля 14-ой варианты = 8,4 – 5,87 = +2,53;

dдля 15-ой варианты = 8,5 – 5,87 = +2,63;

dдля 16-ой варианты = 9,3 – 5,87 = +3,43;

dдля 17-ой варианты = 9,8 – 5,87 = +3,93.

Для второго вариационного ряда:

dдля 1-ой варианты = 1,3 – 4,68 = -3,38;

dдля 2-ой варианты = 2,6 – 4,68 = -2,08;

dдля 2-ей варианты = 3,6 – 4,68 = -1,08;

dдля 4-ой варианты = 3,9 – 4,68 = -0,78;

dдля 5-ой варианты = 4,0 – 4,68 = -0,68;

dдля 6-ой варианты = 4,1 – 4,68 = -0,58;

dдля 7-ой варианты = 4,2 – 4,68 = -0,48;

dдля 8-ой варианты = 4,4 – 4,68 = -0,28;

dдля 9-ой варианты = 4,6 – 4,68 = -0,08;

dдля 10-ой варианты = 4,8 – 4,68 = +0,12;

dдля 11-ой варианты = 4,8 – 4,68 = +0,12;

dдля 12-ой варианты = 4,9 – 4,68 = +0,22;

dдля 13-ой варианты = 5,1 – 4,68 = +0,42;

dдля 14-ой варианты = 5,6 – 4,68 = +0,92;

dдля 15-ой варианты = 6,5 – 4,68 = +1,82;

dдля 16-ой варианты = 7,4 – 4,68 = +2,72;

dдля 17-ой варианты = 7,7 – 4,68 = +3,02.

Результаты заносим в соответствующие колонки таблицы.

4 этап.Полученные отклонения от М (d) возводим в квадрат (d₂).

Для первого вариационного ряда:

d²для 1-ой варианты = = (-3,27)²= 10,6929;

d²для 2-ой варианты = (-3,07)²= 9,4249;

d²для 2-ей варианты = (-2,17)²= 4,7089;

d²для 4-ой варианты = (-1,67)²= 2,7879;

d²для 5-ой варианты = (-1,47)²= 2,1609;

d²для 6-ой варианты = (-1,17)²= 1,3689;

d²для 7-ой варианты = (-0,87)²= 0,7569;

d²для 8-ой варианты = (-0,77)²= 0,5929;

d²для 9-ой варианты = (-0,77)²= 0,5929;

d²для 10-ой варианты = (-0,57)²= 0,3249;

d²для 11-ой варианты = (+0,33)²= 0,1089;

d²для 12-ой варианты = (+0,53)²= 0,2809;

d²для 13-ой варианты = (+2,43)²= 5,9049;

d²для 14-ой варианты = (+2,53)²= 6,4009;

d²для 15-ой варианты = (+2,63)²= 6,9169;

d²для 16-ой варианты = (+3,43)² =11,7649;

d²для 17-ой варианты = (+3,93)²= 15,4449.

Для второго вариационного ряда:

d²для 1-ой варианты = (-3,38)²= 11,4244;

d²для 2-ой варианты = (-2,08)²= 4,3264;

d²для 2-ей варианты = (-1,08)²= 1,1664;

d²для 4-ой варианты = (-0,78)²= 0,6084;

d²для 5-ой варианты = (-0,68)2 = 0,4624;

d²для 6-ой варианты = (-0,58)²= 0,3364;

d²для 7-ой варианты = (-0,48)²= 0,2304;

d²для 8-ой варианты = (-0,28)²= 0,0784;

d²для 9-ой варианты = (-0,08)²= 0,0064;

d²для 10-ой варианты = (+0,12)²= 0,0144;

d²для 11-ой варианты = (+0,12)²= 0,0144;

d²для 12-ой варианты = (+0,22)²= 0,0484;

d²для 13-ой варианты = (+0,42)²= 0,1764;

d²для 14-ой варианты = (+0,92)²= 0,8464;

d²для 15-ой варианты = (+1,82)²= 3,3124;

d²для 16-ой варианты = (+2,72)²= 7,3984;

d²для 17-ой варианты = (+3,02)²= 9,1204

Результаты заносим в соответствующие колонки таблицы.

5 этап.Рассчитываем среднеквадратические отклонения () от средней(М) для каждого из двух вариационных рядов (₁и₂).

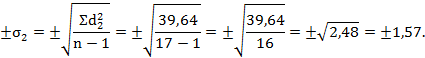
6 этап.Рассчитываем средние ошибки М (m) для каждого из двух вариационных рядов (m₁иm₂).

7 этап.Рассчитываемt-критерий, критерий Стьюдента.

8 этап.По вспомогательной таблице по значениюtнаходим доверительную вероятность (р); перед этим рассчитываем рабочуюn.n= 17 + 17 -2 = 32. Приt,равном 1,74 р>0,05.

9 этап. Заключение:различие средних величин вариационных рядов не достоверно, что означает не доказанную эффективность проведенных профилактических мероприятий.

Расчеты с помощью метода размаха

М₁= 5,87; М₂= 4,68.

Рассчитываем ₁и₂. По вспомогательной таблице находим значение коэффициента К. К при числе наблюдений 17 равен 3,59.

Рассчитываем m₁иm₂.

Рассчитываем t.

Заключение:различие средних величин вариационных рядов не достоверно, что означает не доказанную эффективность проведенных профилактических мероприятий.

Задача № 19

Для решения задачи строим рабочую таблицу. Используем метод ранговой корреляции (Спирмена).

Номер наблюдения	Жилая площадь, приходящаяся на одного проживающего в благоустроенных квартирах, м2 (Х)	Процент часто болеющих детей (Y)	Ранги Х, Rk(x)	Ранги Y, Rk(у)	Разность рангов – Rk(х) – Rk(у) (d)	Квадрат разности рангов (d2)
1	4	21,2	1	13	-12	144
2	5	23,7	2	14	-12	144
3	6	19,6	3	11	-8	64
4	7	20,4	4	12	-8	64
5	8	18,3	5	10	-5	25
6	9	16,5	6	8	-2	4
7	10	17,8	7	9	-2	4
8	11	15,2	8	7	+1	1
9	12	13,9	9	5	+4	16
10	13	14,1	10	6	+4	16
11	14	12,8	11	4	+7	49
12	15	9,6	12	3	+9	81
13	16	7,8	13	2	+11	121
14	17	6,6	14	1	+13	169
n = 14						Σd2 = 902

1 этап.Рассчитываем коэффициент корреляцииR_xyпо формуле Спирмена с использованием полученного значения Σd²= 902.

2 этап.Рассчитываем среднюю ошибкуR_xy.

3 этап.Рассчитываемt.

4 этап.По вспомогательной таблице находим р, которое < 0,001. Степень достоверностиR_xy– высокая.

5 этап.Заключение: связь процента часто болеющих детей с жилой площадью, приходящейся на одного проживающего в благоустроенных квартирах сильная, обратная.

Задача № 20

Модальной для данной выборки является группа крови О.