Semestrovaya

Задание.

Определить количественные показатели надежности , , , по ССН, представленной в таблице 1.

Вариант 1.

Исходные данные.

Рисунок 1 – ССН для определения

Рисунок 2 – ССН для определения

Таблица 1

Элемент ССН	Время работы элемента за 1 цикл эксплуатации, влияющей на		Среднее время восстановления отказа	Количество отказов, влияющих на		Объем испытаний, влияющий на показатели		Примечание
	, мин	, час	, час
1	–	3,0	2,0	–	5	–	5000 км	Расчет по характеристикам 7 элемента
2	2	3,5	5,0	3,0	10	3000 ц	5*105 ч
3	2	1,5	6,0	0	4	600 ц	400 ц
4	1	–	–	0	–	200 ц	–
5	1	1,0	3,0	2,0	5	100 ц	1000 ц
6	–	0,5	10,0	0	2	–	2000 ц
7	20	160	1,5	–	–	–	–

Рисунок 3 – Схема «2 из 3-х» ССН для элемента 7

Таблица 2

,1/час	,1/час	,1/час	,1/час	,1/час	,1/час	,1/час
1210-5	1010-5	2010-5	1510-5	3010-5	2510-5	4010-5

Расчет.

Для расчета надежности элементов 1-6 используем статистические данные, полученные при испытаниях и представленные в задании.

Выполним расчет для элемента 1.

Данные для расчета.

.

Формула для определения коэффициента ремонта i-го элемента имеет следующий вид

(1)

Найдем объем испытаний

Подставим исходные данные в формулу (1)

Среднее квадратическое отклонение

Выполним расчет для элемента 2.

Данные для расчета.

Вероятность безотказной работы i-го элемента при количестве отказов

определяется следующей формулой

(2)

Подставим значения в формулу (2)

Среднее квадратическое отклонение вероятности безотказной работы при

определяется выражением

(3)

Выполним расчет для элемента 3.

Данные для расчета.

Вероятность безотказной работы i-го элемента при количестве отказов

определяется выражением

(4)

А среднее квадратическое отклонение в этом случае определяется следующим выражением

(5)

Подставив численные значение в формулы (4) и (5), получим соответственно

;

.

Коэффициент ремонта:

.

Выполним расчет для элемента 4.

Данные для расчета.

Вероятность безотказной работы i-го элемента при количестве отказов

определяется выражением

Среднее квадратическое отклонение вероятности безотказной работы:

Выполним расчет для элемента 5.

Данные для расчета.

Вероятность безотказной работы i-го элемента при количестве отказов

определяется следующей формулой

(2)

Подставим значения в формулу (2)

Среднее квадратическое отклонение вероятности безотказной работы при

определяется выражением

(3)

Выполним расчет для элемента 6.

Данные для расчета.

Расчет аналогичен расчету надежности для первого элемента. Таким образом, подставим исходные данные в формулу (1) и получим

Выполним расчет для элемента 7.

Структурная схема элемента 7 представляет собой смешанное соединение элементов. Для расчета его надежности представим структурную схему в виде 6 ветвей – А, В, С, D, Е, F – и определим надежность каждой ветви (рис. 4).

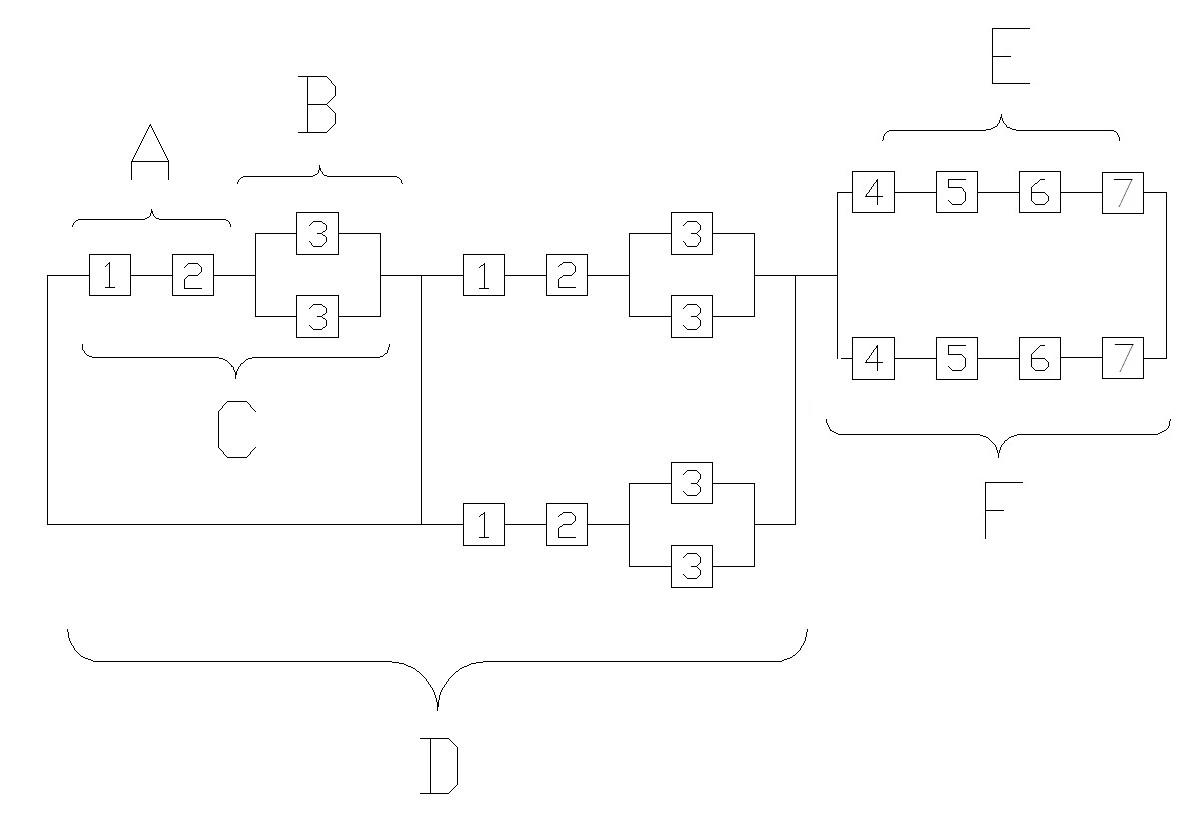
Рисунок 4 – Схема «2 из 3-х» ССН для элемента 7

Данные для расчета.

; ; ; ;

₁ = 1210^-5 1/ч; ₂ = 1010^-5 1/ч; ₃ = 2010^-5 1/ч; ₄ = 1510^-5 1/ч; ₅ = 3010^-5 1/ч; ₆ = 2510^-5 1/ч; ₇ = 4010^-5 1/ч

Значения , определяются из формул, соответственно:

;

.

Ветвь А. Последовательное соединение элементов.

Ветвь В. Схема дублирования.

Функция надежности определяется следующей формулой

, (6)

где

.

Подставим это значение в формулу (6)

.

Ветвь С.

Надежность определяется следующим выражением

.

Ветвь D. Схема «2 из 3».

При такой структурной схеме надежность определяется следующим выражением

.

Среднее квадратическое отклонение

.

Ветвь Е.

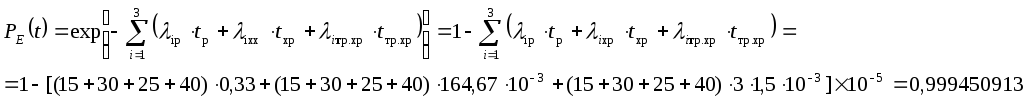
Ветвь F. Схема дублирования.

Функция надежности определяется выражением следующего вида

.

Среднее квадратическое отклонение найдем из выражения

.

Надежность элемента 7.

;

.

Рассчитаем теперь значение коэффициента ремонта системы К_рем для элемента 7 (аналогично расчёту надёжности элемента 7, но с другими значениями параметров t_р и t_хр).

Данные для расчета.

; ; .

Ветвь А. Последовательное соединение элементов.

Ветвь В. Схема дублирования.

;

;

.

Ветвь С.

.

Ветвь D. Схема «2 из 3».

Ветвь Е.

Ветвь F. Схема дублирования.

.

Надежность элемента 7.

.

Вычислим коэффициент ремонта системы 7-го элемента из выражения

. (7)

Для отыскания воспользуемся следующим соотношением

.

Откуда

.

Подставим полученное значение в формулу (7)

;

.

Определим теперь вероятность безотказной работы и среднее квадратическое отклонение вероятности безотказной работы изделия в целом

;

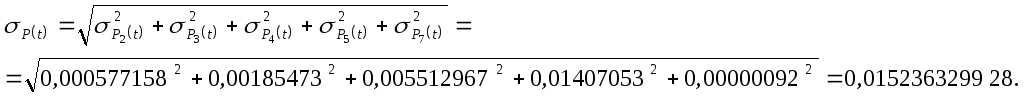
Общий коэффициент ремонта изделия определяется как сумма коэффициентов ремонта элементов, входящих в состав изделия

. (8)

Подставим значения коэффициента ремонта элементов формулу (8)

.

Среднее квадратическое отклонение коэффициента ремонта изделия определяется следующим выражением

Коэффициент регламента определяется выражением вида

. (9)

Подставим значения в формулу (9)

.

Коэффициент готовности найдем из соотношения

. (10)

Подставив численные значения в формулу (10) получим

.

Принимаем

Ответ.

; ; ;

Список использованной литературы

1. Труханов В.М. Надежность в технике. М.: Машиностроение, 1999г. – 598 с.

2. Труханов В.М. Надежность изделий машиностроения. Теория и практика. Учебник для студентов машиностроительных специальностей высших учебных заведений. – М.: Машиностроение, 1996г.– 336с.

3. Труханов В.М. Краткий курс теории и практики надежности сложных систем: Учеб. пособ. / ВолгГТУ. – Волгоград, 1996г. – 118с.

10