3. Лекция 4

1. Многочлены Чебышёва.

Рекуррентная форма записи Многочлены Чебышёва T_n(x), где n � 0, определяются соотношениями

Например,

T₀(x) = 1, T₁(x) = x,

T_n+1(x) = 2xT_n(x) − T_n−1(x) при n > 0.

T₂(x) = 2x² − 1, T₃(x) = 4x³ − 3x,

T₄(x) = 8x⁴ − 8x² + 1, T₅(x) = 16x⁵ − 20x³ + 5x.

(1.11)

Тригонометрическая форма записи. Для любого θ справедливо cos((n+ 1)θ) = 2 cos θ cos nθ − cos((n − 1)θ). При θ = arccos x получим

cos((n + 1) arccos x) = 2x cos(n arccos x) − cos((n − 1) arccos x). (1.12) Рассмотрим выражение cos(n arccos x) при n = 0 и n = 1:

cos(0 · arccos x) = 1 = T₀(x), cos(1 · arccos x) = x = T₁(x). (1.13) Видно, что (1.13) и (1.12) равносильно (1.11), поэтому при всех n T_n(x) = cos(n arccos x).

Явная форма записи. Рекуррентное соотношение (1.11)является раз- ностным. Для его решения заменяют T_n(x) на µⁿ. После подстановки и сокращения получаем:

с корнями

µ² − 2µx + 1 = 0

µ_1,2 = x ± ^/x² − 1.

При x /= ±1 корни простые, поэтому

T_n(x) = c₁(x)µⁿ + c₂(x)µⁿ.

1 2

Из системы

⁽ T₀(x) = 1 = c₁(x) + c₂(x),

T₁(x) = x = c₁(x)(x + ^√x² − 1) + c₂(x)(x − ^√x² − 1).

следует, что c₁ = c₂ = 1/2. Таким образом,

(x + ^/(x² − 1))ⁿ + (x − ^/(x² − 1))ⁿ

T_n(x) = ₂ .

Свойства:

1. T_2n(x) — чётные функции, T_2n+1(x) — нечётные функции.

2. T_n(x) выражается через косинус, следовательно |T_n(x)| � 1 при x ∈

[−1, 1].

3. Из уравнения T_n(x) = cos(n arccos x) = 0 получаем, что

(2k − 1)π

— нули T_n(x).

x_k = cos _2n

, k = 1, . . . , n

4. Из уравнения T ¹ (x) = − sin(n arccos x)^√−n

= 0 получаем, что

n

ξ_k = sin

_kπ

n

1−x²

, k = 0, . . . , n

— точки экстремума T_n(x). Заметим, что T_n(ξ_k) = (−1)^k.

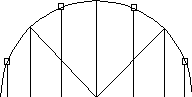
Геометрическая интерпретация. Если верхнюю полуокружность еди- ничного радиуса разделить на n частей, то середины дуг — координаты нулей, экстремумы — точки деления (рис. 1.7).

Наименьшее отклонение от нуля Так как T₀(x) = 1 и T_n+1(x) = 2xT_n(x) −. . ., то коэффициент при главном члене равен 2ⁿ⁻¹. В погрешно- сти многочлена Лагранжа участвует многочлен ω_n+1 = (x−x₀)·. . .·(x−x_n)

с старшим коэффициентом 1. Поэтому рассматривают также изменённый многочлен Чебышёва T_x(n) = 2¹⁻ⁿT_n(x) со старшим коэффициентом 1.

Справедлива следующая

ξ₄ ^x₄ ^ξ₃

x₃ ξ₂

^x₂ ξ₁

x₁ ξ₀

Рис. 1.7: Геометрическая интерпретация корней и точек экстремума поли- нома Чебышёва при n = 4.

Теорема 4.5. Для всякого многочлена P_n(x) степени n с единичным старшим коэффициентом имеет место неравенство

max

x∈[−1,1]

|P_n(x)| � max

x∈[−1,1]

|T _n(x)| = 2¹⁻ⁿ,

причём знак равенства возможен только в случае P_n(x) = T_n(x).

Доказательство «�». Будем действовать от противного. Пусть найдётся такой многочлен, что

max

x∈[−1,1]

|P_n(x)| < max

x∈[−1,1]

|T _n(x)| = 2¹⁻ⁿ. (1.14)

Рассмотрим многочлен Q_n−1(x) = T_n(x) − P_n(x) степени не выше n − 1

(оба слагаемых имеют старший единичный коэффициент). Подставим в

него точки ξ^k = sin ^kπ , k = 0, . . . , n (точки экстремума многочлена T_n(x)):

n _n

i k 1−n

_k из-за (1.14)

sign(Q_n−1(ξ_n)) = sign((−1) 2

− P_n(ξ_n))

=

= sign((−1)^k2¹⁻ⁿ) = (−1)^k.

Заметим, что знак многочлена Q_n−1(x) меняется n + 1 раз на отрезке [−1, 1] (т.к. k = 0, . . . , n). Значит, многочлен Q_n−1(x) степени не выше n − 1 имеет n различных корней. Получили противоречие.

Доказательство единственности.

Из-за последней теоремы многочлен T_n(x) получил название наименее уклоняющегося от нуля.

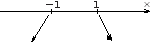
a

_x′ ₌ ^b+a

b x^′

b−a

a

2x^′−(b+a)

_{b x}′

₂ ⁺ ₂ ^x x =

b−a

Рис. 1.8: Линейные преобразования отрезка [−1, 1] в [a, b] и обратно

Заметим, что теорема работает только на отрезке [−1, 1]. Хочется снять это ограничение. Для этого рассматривают линейные преобразования от-

резка [−1, 1] в [a, b] x¹ = ^b+a

+ ^b−ax и обратно x = ^2xt^−(b+a) . Получаем

2 2

многочлен

b−a

[a,b]

b − a ⁿ

2x − (b + a)

n 1−2n

2x − (b + a)

T_n (x) = ₂ T_n

b − a

= (b − a) 2 T_n

b − a

со старшим коэффициентом 1, наименее уклоняющийся от нуля на отрез- ке [a, b]. Будем называть T ^[a,b](x) также чебышёвским. Нетрудно прове- рить, что нулями многочлена T ^[a,b](x) являются точки

n

n

x_k =

b + a

+

2

b − a _cos 2

(2k − 1)π

2n

, k = 1, . . . , n. (1.15)

Теперь можно дать ответ на вопрос, как уменьшить погрешность ин- терполяции R_n(x) за счёт выбора узлов интерполяции. Если в качестве узлов интерполяции выбрать корни (1.15) многочлена T ^[a,b](x), тогда

n

max |ω_n+1(x)| = max |T _n (x)| = (b − a)ⁿ⁺¹2^1−2(n+1).

[a,b]

a�x�b

a�x�b

При этом улучшить (т.е. уменьшить) последнюю величину уже нельзя.

Получаем |R_n(x)| � ^Mn+1 (b − a)ⁿ⁺¹2^1−2(n+1), где M_n+1 = max |f ⁽ⁿ⁺¹⁾(x)|.

(n+1)!

a�x�b

2. Среднеквадратическое приближение (метод наименьших квадратов)

Рассмотрим принципиально иной способ приближения функций, задан-

ных таблицей своих значений

. Будем искать приближе-

ние в виде полинома степени m: P_m(x) = a₀ + a₁x + . . . + a_mx^m, такого,

который минимизирует сумму квадратов отклонений полинома от задан- ных значений функции:

n

Φ(a₀, a₁, . . . , a_m) = ^,(P_m(x_i) − y_i)².

i=0

Ясно, что при m = n решением задачи является полином Лагранжа, поскольку на нём достигается абсолютный минимум: Φ = 0. Известно, что при m < n задача имеет единственное решение. При m > n задача имеет бесконечное множество решений.

Рассмотрим случай m < n. Условия минимума функции Ф следуют из математического анализа:

n

= 2 ^,(P_m(x_i) − y_i)x^k = 0, k = 0, 1, ..., m.

i

∂Φ

∂a_k

i=0

После подстановки выражения для P_n(x) и перегруппировки слагаемых, получим:

n

_a0 ^, _xk+0

_i + a₁

i=0

n

,

i=0

x^k+1 + . . . + a_m

n

,

i=0

_xk+m _{= a0}

n

,

i=0

y_ix^k, k = 0, . . . , m.

Эта система линейных уравнений с симметричной матрицей:

i

i

i

 n + 1 ^), x_i · · · ^), x^m

i

  _a0

 _{), y}i

^ ), ), ₂

^ _i · · ·

x_i x



_{), m+1}   

_i   

x

a₁

  

 _{), y}i_xi

 





_ ), i), i

^), m+2 ^{ }

  ^), i

 x²

x³ · · ·

x_i   a₂

 ⁼ 

y_ix²  ^.

. .

.

.



^ . .

. _{. .}

_.   _.   _. 

    

.

.

.

.

.

.

 _), xm

^), _xm+1

m+m ^{ }

  _), m

_{i i} · · · ^), x_i a_m

y_ix_i

Полином степени m < n с коэффициентами, найденными таким обра- зом, называется среднеквадратичным приближением функции, заданной таблицей. (Или наилучшим среди полиномов степени m приближением к функции по табличным данным.)

Соответствующую погрешность приближения можно характеризовать

n

среднеквадратичным отклонением ∆ = ^{1 ),}[P_m(x_i) − y_i]².

n+1

i=0

Основная сфера применения — обработка экспериментальных данных.

Экспериментальные данные характеризуются значительным разбросом (ошибки измерения, экспериментальный «шум» и т.д.) Интерполяцион- ный полином, построенный по этим точкам, плохо отражает поведение функции f (x). Среднеквадратичный полином «сглаживает шум».

Пример. Пусть известно, что величина y является некоторой функцией от аргумента x, причём в результате измерений получена таблица значе- ний y_k = y(x_k), k = 1, 2, 3, 4.

Полученные измерения позволяют приближённо считать, что зависи- мость y = y(x) является линейной, т.е.

y = ax + b, (1.16)

где a, b - некоторые числа. Числа a, b в эмпирической формуле (1.16) необходимо подобрать таким образом, чтобы при значениях x = x_k (k = 1, 2, 3, 4) выполнялись условия:

ax₁ + b = y₁, ax₂ + b = y₂, ax₃ + b = y₃, ax₄ + b = y₄. (1.17)

Получилась система четырёх линейных уравнений относительно двух неизвестных a, b. Классического решения данной системы нет.

4

Введем функцию Φ(a, b) =

^), (ax_k + b − y_k)², равную сумме квадратов

k=1

невязок, и примем за обобщённое решение системы (1.17) ту пару чи-

сел (a, b), для которой функция Φ(a, b) принимает наименьшее значение. Получим систему двух уравнений:

∂Φ

∂a

= 0,

.. _∂Φ

∂b

= 0.

Данная система имеет обычное классическое решение.

3. Многочлены Эрмита

Предположим, что функция задана конечным набором своих значений, а также некоторых производных (возможно, не во всех точках). В таблице, K_i определяет количество данных в i-ом узле. Например, если в узле x_i

заданы значение функции y_i и производной y¹, то K_i = 2. Для всякого

i

i = 0, . . . , n K_i � 1, т.е. в каждой колонке обязательно присутствует y_i — значение функции в точке x_i. Обозначим p = K₁ + K₂ + . . . + K_n − 1.

Многочлен H_p(x) степени p называется многочленом Эрмита, если

_H(k)

(k)

_p (x) = y_i , i = 0, . . . , n, k = 0, 1, . . . , K_i − 1.

Погрешность для многочлена Эр- мита выражается аналогично по- грешности для многочлена Лагран- жа. Если интерполяция происхо- дит на отрезке [a, b], содержащем x_i, i = 0, . . . , n и функция f (x) (p+1) раз непрерывно дифференци- руема, то погрешность выражается формулой:

x	x0	x1	· · ·	xn
y	y0 y1 0 ... y(K0−1) 0	y1 y1 1 ... y(K1−1) 0	· · ·	yn y1 n ... y(Kn−1) 0
y1			· · ·
y11			· · ·
y111
...			· · ·
	K0	K1	· · ·	Kn

R_p(x) = f (x) − H_p(x) =

_f (p+1)_(ξ)

(x x )^K0

− ₀

(p + 1)!

(x − x₁)^K1

. . . (x − x_n)^Kn,

где ξ неизвестная точка принадлежащая интервалу [a, b]. Принято обозна- чать ω_p+1(x) = (x − x₀)^K0 (x − x₁)^K1 . . . (x − x_n)^Kn .

4. Интерполяция кубическими сплайнами

Сплайном, соответствующим данной функции f (x) и данным узлам x₀, . . . x_n, называется функция s(x), удовлетворяющая следующим условиям:

1. на каждом сегменте [x_i−1, x_i], i = 1, 2, . . . , n,функция s(x) является многочленом третьей степени;

2. функция s(x), а также её первая и вторая производные непрерывны на [a, b];

3. s(x_i) = f (x_i), i = 0, 1, . . . , n.



 ^s_i^(x_i^{) = f (x}_i^),

^ _s1 1

_i(x_i) = s_i−1(x_i),

^ s_i (x_i) = s_i

₁(x_i).

11 11



−