На сортировку / 2102172 / LABA_5

MINISTRY OF EDUCATION AND SCIENCE OF THE REPUBLIC OF KAZAKHSTAN

ALMATY UNIVERSITY OF POWER ENGINEERING AND TELECOMMUNICATION

Department of Higher mathematics

Discipline “SDEUOC”

Laboratory work №4

Theme: Tasks of integral calculus, operational calculus and differential equations

Option № 3

Performed by: Abdesh B.O. Ea-15-11

Checked by: ass. prof. Kim R.E.

Almaty, 2016

Task 7.

No answer

Task 9.

1. Solve the system differential equation using the procedure Given/Odesolve. Initial conditions same for all options: y₁(0)=2, y₂(0)=1.

2. Create a table of values and function arguments.

3. Find the value of the function obtained at t = 3.4, or select a point on their own.

4. Build charts derived functions.

5. Build system phase portrait.

The job processing

Given

- system equation

-initial conditions

- solution of system

- step argument is equal 0.1

- value functions at the point

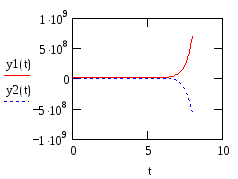- graphs of function

- phase portrait of system

Answer:

Table and graphs cm. higher.

Task 10.

1. Solve the differential equation using the function rkfixed program Mathcad. Initial conditions same to all options:

x1(0)=3, x2(0)=1.

2. Create a table of values and function arguments.

3. Find the value of the function obtained at t = 4.2.

4. Build charts derived functions.

5. Build system phase portrait.

The job processing

- specifies the numbering of rows and columns with №1 in the table (matrix) solutions

- matrix-columns in initial conditions

- matrix-columns range 2x1 the right side of the system

• - amount of points in the interval {0;10}

- location of function x1 and x2

Function rkfixed creates matrix numbers, where columns is the value of the argument and the values of the desired functions. In Mathcad this columns denoted given above function u in the form of . For the similarity with the original features denote them in the form:

- column arguments

- column value function x1

- column value function x2

_{X1(4.2) = 2.285}

_{X2(4.2)= 0.815}

-graph function x1 and x2

-phase portrait system

Answer: _{X1(4.2) = 2.285}

_{X2(4.2)= 0.815}