
На сортировку / 2102172 / to3BDK_1
.docxНекоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра теоретических основ электротехники
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №3
по дисциплине: Анализ электрических цепей и электрического поля
на тему: Теория электромагнитного поля
Специальность: 5В071800 - Электроэнергетика
Выполнил: ст. гр. Э-14-7 Бектенов Д.К.
№ зачетной книжки: 144179
Руководитель: ст. пр. Болдырева Л. П.
«____» ___________________ 20___г.
Алматы, 2016
Содержание
1. Исходные данные………………………………………………………………3
2. Расчет электростатических полей……………………………………………..3
3. Расчет магнитного поля уединенного бесконечно длинного прямого провода…………………………………………………………………………….8
4. Заключение…………………………………………………………………….11
5. Список литературы………………………………………………………….12

Исходные данные
Таблица 1 – Исходные данные для варианта К-05
|
Б |
7 |
9 |
|
Задачи: 4.1б; 4.5б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RD=0,96 м |
|
|
γ2.=6∙10-2. Cм∙,м-1. |
|
|
|
μ=150 |
|
|
|
|
|
|
|
Задача 4.1б – Расчет электростатических полей
4.1 Поле электрических зарядов вблизи границы раздела двух диэлектриков.
Параллельно
плоской границе раздела двух сред с
диэлектрическими проницаемостями
 1=9
и
1=9
и
 2=7
протянуты два параллельных длинных
провода одинакового сечения с радиусом
R=710-3
м на расстоянии d=0,8
м и на расстоянии h1=0,
6 м и h2=0,98
м от граничной плоскости. Проводам
сообщены заряды
2=7
протянуты два параллельных длинных
провода одинакового сечения с радиусом
R=710-3
м на расстоянии d=0,8
м и на расстоянии h1=0,
6 м и h2=0,98
м от граничной плоскости. Проводам
сообщены заряды
 1=-510-9
Кл/м и
1=-510-9
Кл/м и
 2=
710-9
Кл/м. Взаимное расположение проводов и
плоскости раздела двух сред показано
на рисунке 1.
2=
710-9
Кл/м. Взаимное расположение проводов и
плоскости раздела двух сред показано
на рисунке 1.

Рисунок 1
При расчете электростатических полей в неоднородных средах, когда электрические заряды расположены вблизи границы раздела двух сред с различными электрическими свойствами применяется метод изображений.
Идея метода изображений заключается в том, что вместо неоднородной среды рассматривается среда однородная, влияние неоднородности учитывается введением фиктивных зарядов.
Определение плотности связанных зарядов связ в точке К на граничной плоскости.
Плотность связанных зарядов равна:

где
P1n,
P2n
- нормальные составляющие векторов
поляризации в среде с диэлектрической
проницаемостью
 1
и в среде с диэлектрической проницаемостью
1
и в среде с диэлектрической проницаемостью
 2.
2.

Отсюда

где
 ,
так как плотность свободного заряда на
граничной плоскости равна 0;
,
так как плотность свободного заряда на
граничной плоскости равна 0;
 нормальные
составляющие векторов напряженности
электрического поля на граничной
плоскости в средах с диэлектрическими
проницаемости
нормальные
составляющие векторов напряженности
электрического поля на граничной
плоскости в средах с диэлектрическими
проницаемости
 .
.
Напряженность
 рассчитывается от заданных зарядов
рассчитывается от заданных зарядов
 и фиктивных зарядов
и фиктивных зарядов
 (рисунок 2).
(рисунок 2).



Рисунок 2
Напряженности
 рассчитываются по формулам:
рассчитываются по формулам:


Координаты точки К: ХК=0,5 , УК=0.
Нормальные
составляющие
 равны:
равны:

Знак
зарядов
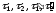 учтен при изображении векторов
учтен при изображении векторов
 на
рисунке 2.
на
рисунке 2.
Отсюда Е1n равна:

Напряженность Е2n рассчитывается от фиктивных зарядов

При
этом рассматривается однородная среда
с диэлектрической проницаемостью
 (рисунок 3)
(рисунок 3)

Рисунок 3
Напряженности
 равны:
равны:

Нормальные
составляющие напряженностей
 и Е2n
вычисляются по формулам:
и Е2n
вычисляются по формулам:

Отсюда определим плотность связанных зарядов в точке К на граничной плоскости
 .
.
4.5 б – Расчет магнитного поля уединенного бесконечно длинного прямого провода
Построим
качественно картину магнитного поля
уединенного бесконечно длинного прямого
провода круглого сечения, по которому
протекает постоянный ток I. Окружающая
среда - воздух. По условиям симметрии
линии напряженности магнитного поля
 представляют
собой концентрические окружности,
центры которых расположены на оси
провода. Линии напряженности магнитного
поля
представляют
собой концентрические окружности,
центры которых расположены на оси
провода. Линии напряженности магнитного
поля
 лежат в плоскостях перпендикулярных
оси провода. Направление вектора
лежат в плоскостях перпендикулярных
оси провода. Направление вектора
 определяется по правилу буравчика
(рисунок1). Аналогично можно построить
линии магнитной индукции
определяется по правилу буравчика
(рисунок1). Аналогично можно построить
линии магнитной индукции
 - магнитная постоянная;
- магнитная постоянная;
 -
относительная магнитная проницаемость).
-
относительная магнитная проницаемость).

Рисунок 1
Расчет
внутренней индуктивности провода.
Рассчитаем внутреннюю индуктивность
участка провода длиной
 .
.
Магнитный
поток внутри провода на участке длиной
 (рисунок 2) равен:
(рисунок 2) равен:

где
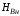 - вектор напряженности магнитного поля;
- вектор напряженности магнитного поля;
 направлен
перпендикулярно сечению провода “от
нас”.
направлен
перпендикулярно сечению провода “от
нас”.
Вектор
 направлен также перпендикулярно сечению
провода.
направлен также перпендикулярно сечению
провода.

Рисунок 2
Рассчитаем
поток
 :
:

Расчет потокосцепления Вн внутри провода.
Потокосцепление Вн внутри провода определим по формуле:

где
 - ток, протекающий через поперечное
сечение провода, с радиусом r;
- ток, протекающий через поперечное
сечение провода, с радиусом r;
 -
элементарный магнитный поток, пронизывающий
поверхность площадью ds=
-
элементарный магнитный поток, пронизывающий
поверхность площадью ds= dr.
dr.
Отсюда

Внутренняя индуктивность Lвн участка провода связана с потокосцеплением Вн уравнением:
Вн= LвнI . (5)
Отсюда

Заключение
В данной расчетно-графической работе я получил навыки для расчета электрических и магнитных полей и рассчитал магнитное поле постоянного тока. По координатным данным рассчитал плотность связанных зарядов, а так же определил внутреннюю индуктивность участка провода длинной l=1м.
Список литературы
-
К. С. Демирчян, Л. Р. Нейман, Н. В. Коровкин, В. Л. Чечурин. Теоретические основы электротехники. – том 2. – СПб.: Питер, 2003.-576с
-
К. С. Демирчян, Л. Р. Нейман, Н. В. Коровкин, В. Л. Чечурин. Теоретические основы электротехники. – том 3. – СПб.: Питер, 2003.-377с
-
В. И. Денисенко, Е. Х. Зуслина, Л. П. Болдырева ТОЭ3. Рассчет электрических цепей и электромагнитных полей. Методическое указание и задания к РГР №1-5. – Алматы: АУЭС, 2012.-24



 =9
=9

 =7
=7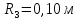

 =
=












