§ 3.1. Скорость химических реакций

Скорость химической реакции характеризует изменение концентрации веществ (реагентов и продуктов реакции) во времени. Различают реакции в газовых смесях или растворах (гомогенные реакции) и гетерогенные реакции, когда хотя бы один реагент находится в иной фазе, чем другие (газ-жидкость, твердое тело-жидкость).

Скорость гомогенной реакции измеряется изменением концентрации реагентов (или продуктов) в единицу времени. В гетерогенных реакциях контролируется изменение концентрации газовых или находящихся в растворе компонентов:

.

Скорость реакций зависит от природы и концентрации реагирующих веществ, температуры, давления (для газовых реакций), величины поверхности раздела фаз (для гетерогенных реакций), а также от присутствия и количества катализаторов или ингибиторов.

Зависимость скорости реакции от концентрации реагентов выражается законом действия масс - для реакции aA + bB  cC :

,

т.е. скорость реакции пропорциональна концентрации реагирующих веществ.

k - фактор пропорциональности, представляет собой удельную скорость реакции (константу скорости), т.е. скорость реакции при единичных концентрациях компонентов A и B. В отличие от скорости реакции константа k не зависит от концентрации растворов и является количественной характеристикой процесса. В гетерогенных реакциях концентрации конденсированных компонентов (твердых тел или несмешивающихся жидкостей) в уравнении закона действия масс не учитываются. Так, скорость реакции

CaO ^(тв) + H₂O ^(ж)  Ca(OH)₂

зависит только от площади поверхности твердой CaO и интенсивности перемешивания смеси.

Зависимость константы скорости реакции от температуры описывается уравнением Аррениуса:

,

где Z₀ - количество соударений молекул (ионов, атомов) реагентов в секунду в единице объема, p - стерический фактор, показывающий, какая доля всех соударений благоприятна для данной реакции, e - основание натуральных логарифмов, R - газовая постоянная, T - температура (в K), E_акт - энергия активации реакции.

Энергия активации - избыточный запас энергии по отношению к средней энергии молекул реагентов, достаточный для протекания реакции. Любая реакция протекает через образование переходного состояния реакции (активационная стадия) - т.е. состояние, в котором старые связи окончательно не разорвались, а новые еще не образовались:

A + B [A Ч Ч Ч B] ^№ ® C.

Энергия активации определяется при измерении нескольких констант скорости при разных температурах либо графически из зависимости ln(k)-1/T, либо аналитически из уравнения Аррениуса для каждой пары температур.

Зависимость скорости от температуры для многих реакций подчиняется эмпирическому правилу Вант-Гоффа: при изменении температуры на 10 градусов скорость реакции изменяется в 2 . . . 4 раза, т.е.

,

где температурный коэффициент g = 2 . . . 4.

Большинство химических процессов в определенных условиях может протекать обратимо:

A + B C + D.

В этом случае в системе имеют место как прямая, так и обратная реакции, причем по мере превращения скорость прямой реакции убывает, а обратной - возрастает. При уравнивании обеих скоростей возникает состояние динамического равновесия - количество образовавшихся продуктов реакции (C и D) в единицу времени равно количеству распавшихся на исходные вещества (A и B).

Химическое равновесие реакции aA + bB cC + dD характеризуется константой равновесия:

.

В зависимости от необходимости различают K_c (константа равновесия, учитывающая концентрации реагирующих партнеров), K_p (константа, учитывающая парциальные давления газов) и K_f (константа, учитывающая мольные доли компонентов):

, .

При этом между K_c, K_p и K_f существует простая связь:

,

,

где Dn - разность между суммой коэффициентов компонентов реакции (Sn_прод - Sn_исх), p₀ - общее давление газовой смеси. При Dn =0 (реакция идет без изменения числа молей) K_c=K_p=K_f . В этом случае

.

В общем же случае при постоянной температуре

.

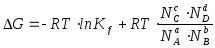Примеры решения задач

Задача 3.1.

Как изменится скорость реакции 2A_{(раствор)} + 3B_{(раствор)} ® 4C_{(раствор)} (исходные концентрации [A]=5 моль/л, [B]=6 моль/л) после израсходования 60% компонента A?

Решение: по уравнению реакции на 2 моль A расходуется 3 моля B. Прореагировало 5 Ч 0.6 = 3 моля A. Из пропорции:

2 моля A - 3 моля B,

3 моля A - x молей B

находим x = 4.5 молей B.

Таким образом, в реакционной смеси осталось (5-3)=2 моля A и (6-4.5)=1.5 моля B. В соответствии с законом действия масс начальная скорость реакции

.

После того, как прореагировало 60% А:

,

.

Таким образом, скорость реакции уменьшится в 400 раз.

Задача 3.2.

Написать выражения закона действия масс для реакций:

1. 2 CO_(газ) + O_2(газ) ® 2 CO_2(газ),

2. CO_2(газ) + C_(тв) ® 2 CO_(газ) ,

3. CaO_(тв) + H₂O_(ж) ® Ca(OH)_2(тв) ,

4. NaOH_{(раствор)} + HCl_{(раствор)} ® NaCl_{(раствор)} + H₂O_(ж) .

Решение: в первой реакции участвуют реагенты в газовом состоянии (система гомогенная), следовательно:

.

Вторая реакция проходит в гетерогенных условиях (газ - твердое тело). Так как в химических процессах меняются только концентрации компонентов, находящихся в газовых смесях или в растворах (концентрация несмешивающихся жидкостей, а также твердых компонентов постоянна), выражение закона действия масс для этой реакции

.

Реакция CaO + H₂O ® Ca(OH)₂ гетерогенна: участвуют жидкость (H₂O) и твердое тело (CaO), концентрации которых в процессе не изменяются. Следовательно:

.

В последнем случае реакция гомогенна (раствор):

.

Задача 3.3.

Как изменится скорость реакции 2A_(газ)+3B_(газ)®C_(газ) при повышении давления в 2 раза?

Решение: увеличение давления в газовой реакции связано с уменьшением реакционного объема; при сохранении количества веществ это означает увеличение их концентрации. При увеличении давления в 2 раза концентрация А и В увеличится вдвое. Следовательно:

,

.

Скорость реакции увеличится в 32 раза.

Задача 3.4.

Как изменится скорость реакции A_(тв)+2B_(газ)®3С_(тв) при уменьшении давления в 3 раза?

Решение: при уменьшении давления уменьшится концентрация только газового компонента В, т.е. [B] уменьшится втрое.

,

.

Скорость реакции уменьшится в 9 раз.

Задача 3.5.

Как изменится скорость реакции 2 A + 3 B ® С при повышении температуры с 40 до 80°С (температурный коэффициент Вант-Гоффа равен 2)?

Решение: в соответствии с правилом Вант-Гоффа

; .

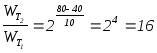Скорость реакции повысится в 16 раз.

Задача 3.6.

Как следует изменить температуру, чтобы понизить скорость химической реакции в 1024 раза (g=2)?

Решение: ;

; ,

;

; .

Температуру реакции следует понизить на 100 градусов.

Задача 3.7.

Как изменится скорость реакции 4A_(газ)+3B_(газ)®3С_(газ) при повышении температуры на 35°С и понижении давления в 2 раза? (Температурный коэффициент скорости равен 3).

Решение: при повышении температуры скорость реакции увеличится:

.

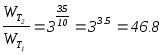При понижении давления скорость реакции уменьшится:

,

; .

Следовательно .

При одновременном изменении давления и температуры скорость реакции составит 0.3656 от исходной.

Задача 3.8.

Найти энергию активации реакции, если при 20°С константа скорости реакции составляет 2,5 Ч 10^-2, а при 30°С - 5,0 Ч 10^-2 л/м Ч с?

Решение: в соответствии с законом Аррениуса

; ;

;

.

Вычтем из второго уравнения первое:

,

,

51 134 Дж/моль = 51.134 кДж/моль.

Задача 3.9.

В реакции 2A_(газ)+B_(газ) 3С_(газ) равновесные концентрации составляют:

[A]=5 моль/л,

[B]= 3 моль/л,

[C]= 4 моль/л.

Найти константу равновесия (K_c).

Решение: .

Задача 3.10.

Найти константу равновесия (K_p) реакции 2A_(газ)+3B_(газ)С_(газ), если после установления равновесия в смеси содержится 30% А, 20% В и 50% С по объему при общем давлении 2 атм.

Решение: .

Парциальные давления компонентов, учитывая закон Авогадро, составляют:

P_i = P_общ Ч C_мол = P_обш Ч C_об.%,

P_A = 2 Ч 0.3 = 0.6 атм,

P_B = 2 Ч 0.2 = 0.4 атм,

P_C = 2 Ч 0.5 = 1.0 атм.

Отсюда:

.

Задача 3.11.

Найти константу равновесия в газовой реакции 2A+5B3C+D, если исходные концентрации [A]=5моль/л, [B]=7моль/л, и к моменту установления равновесия прореагировало 30% А.

Решение: к моменту установления равновесия прореагировало 5 Ч 0.3 = 1.5 моль/л компонента А. Найдем количество прореагировавшего компонента В и образовавшихся С и D. По уравнению реакции

на 2 моля А расходуется	- 5 молей В;
1.5 моля A	- x молей В;	=> ;
из 2 молей А образуется	- 3 моля С;
1.5 моля A	- y;	=>;
из 2 молей А образуется	- 1 моль D;
1.5 моля A	- z;	=> z=0.75.

Следовательно, равновесные концентрации реагентов составляют:

[A]_равн = 5 - 1.5 = 3.5 моль/л;

[B]_равн = 7 - 3.75 = 3.25 моль/л;

[C]_равн = 2.25 моль/л;

[D]_равн = 0.75 моль/л.

Тогда .

Задача 3.12.

Используя стандартные значения DH⁰ и DS⁰, рассчитать константу равновесия реакции N₂+3H₂2NH₃ при 1000°С. (Зависимостью DH и DS от температуры пренебречь).

Решение: N_2(газ) + 3 H_2(газ) 2 NH_3(газ).

ѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕ

DH^обр

(кДж/моль) 0 0 -46

ѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕ

S^обр 192 131 192

(Дж/моль Ч К)

ѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕѕ

DH_р = -92 кДж/моль,

DS = 2 Ч S^обр_NH3 - S^обр_N2 - 3 Ч S^обр_H2 = 2 Ч 192 - 192 - 3 Ч 131 =

= -201 Дж/моль Ч К = -0.201 кДж/моль Ч К,

DG = DH - TDS = -92 + 0.201 Ч 1273 =

= 163.87 кДж/моль,

DG = - RT Ч ln k,

.

Константа равновесия реакции .

Задача 3.13.

При 100°С константа равновесия реакции A+B2C равна 4. Найти равновесные концентрации А, В и С, если исходные концентрации [A]₀=[B]₀ = 2 моль/л.

Решение: .

Примем [C]_равн = x моль/л, тогда количество прореагировавших А и В определяем как x/2 молей и равновесные концентрации [A] и [B] = (2- x/2) моль/л.

Подставив эти величины в выражение константы равновесия, получим

,

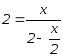, откуда x = 2.

Следовательно:

[C]_равн = 2 моль/л;

[A]_равн = [B]_равн =(2 - 2/2) = 1 моль/л.

Растворы - это гомогенные системы переменного состава. Для характеристики относительного содержания компонентов растворов используют различные методы выражения концентраций:

Массовые (объемные) проценты (%_масс, %_об) - процентное содержание растворенного вещества, отнесенного ко всему раствору;

Молярная концентрация (M, моль/л) - количество молей растворенного вещества в 1 л раствора;

Нормальная концентрация (н, моль/л) - количество эквивалентов вещества, содержащихся в 1 л раствора;

Моляльная концентрация (m, моль/кг) - количество молей растворенного вещества, приходящееся на 1 кг растворителя;

Мольная доля (N_i) - количество молей растворенного вещества или растворителя, отнесенное к общей сумме молей.

Связь между свойствами растворов и их концентрацией может быть выражена несколькими уравнениями:

Для растворов неэлектролитов:		Для растворов электролитов:
	1-й закон Рауля

Здесь P₀ - давление насыщенного пара над растворителем, P - давление пара над раствором, N₂ - мольная доля растворенного вещества, i - изотонический коэффициент.

Dtфп = K Ч m	2-й закон	Dtфп = i Ч K Ч m
Dtкип = E Ч m	Рауля	Dtкип = i Ч E Ч m
Dtкрист = K Ч m		Dtкрист = i Ч K Ч m

Здесь Dt_кип = t_{кип. раствора} - t_{кип. растворителя},

Dt_крист = t_{крист. растворителя} - t_{крист. раствора},

E - эбулиоскопическая постоянная растворителя,

K - криоскопическая постоянная растворителя.

Осмотический закон Вант-Гоффа

P_осм=C Ч R Ч T; P_осм= i Ч C Ч R Ч T.

где P_осм - осмотическое давление, С - молярная концентрация растворенного вещества, R - газовая постоянная.

Различие между растворами неэлектролитов и электролитов обусловлено присутствием в последних большего числа частиц вследствие электролитической диссоциации молекул растворенного вещества (при одинаковой концентрации обоих растворов).

.

При этом ,где i=1 для неэлектролитов, i>1 для электролитов.

Между константой диссоциации, степенью диссоциации и изотоническим коэффициентом существуют простые связи:

(для слабых электролитов ),

, где N = m + n.

Вода - лучший растворитель, обладающий высокой ионизирующей способностью, является чрезвычайно слабым электролитом:

H₂O H⁺ + HO^-,

а точнее 2H₂O H₃O⁺ + HO^-.

Степень диссоциации воды » 2 Ч 10^-9 при комнатной температуре. Поэтому произведение концентраций ионов воды является постоянной величиной (ионное произведение воды):

K_H2O = [H⁺] Ч [HO^-] = 10^-14 (при 22°C).

Концентрация ионов водорода H⁺, а чаще водородный показатель pH=-lg(C_H+) используется как мера кислотности среды:

в нейтральной среде [H⁺]=[HO^-]=10^-7; pH = 7,

в кислой среде [H⁺]>[HO^-] >10^-7; pH < 7,

в щелочной среде [H⁺]<[HO^-] <10^-7; pH > 7.

В этих средах [H⁺]= K_H2O / [HO ^-]=10 ^-14 / [HO ^-], pH = 14 - pOH.

Для труднорастворимых сильных электролитов произведение концентраций ионов в растворе (K_nA_m) при постоянной температуре - величина постоянная (произведение растворимости ПР), качественно указывающая на растворимость этого электролита при данной температуре:

K_nA_m nK^m+ + mA^n-,

ПР = [K^m+]ⁿ Ч [A^n-]^m.

Низкие значения ПР указывают на слабую растворимость электролита. Вещество полностью растворится, если произведение концентраций ионов в растворе меньше ПР, и выпадает в осадок, если это произведение больше ПР.

При растворении солей в воде наряду с диссоциацией молекул на ионы в ряде случаев имеет место обмен ионами между солью и водой (гидролиз солей):

KA + H₂O KOH + HA.

Учитывая, что в этом равновесном процессе самым слабым электролитом является вода, легко понять невысокие степени гидролиза солей. Степень гидролиза достигает значительных величин лишь в условиях больших разбавлений растворов, при повышенных температурах и малой растворимости продуктов гидролиза.

Рассмотрим несколько примеров гидролиза солей:

А. При гидролизе могут образовываться только сильные кислоты и основания:

K⁺ + A^- + H₂O K⁺ + HO^- + H⁺ + A^-.

Наличие в системе лишь одного слабого электролита (воды) смещает равновесие в сторону исходной соли - гидролиз не идет.

Б. При гидролизе образуется слабое основание и сильная кислота:

K⁺ + A^- + H₂O KOH + H⁺ + A^-

или K⁺ + H₂O KOH + H⁺,

pH<7.

Следовательно, регулятором гидролиза является образование некоторого количества слабо-диссоциирующего основания и понижение pH среды (среда кислая).

Соли, содержащие многовалентные катионы, образуют при гидролизе основные соли:

ZnCl₂ + H₂O Zn(OH)Cl + HCl,

Zn²⁺ + H₂O (ZnOH)⁺ + H⁺.

Гидролиз по 2-ой стадии

(ZnOH)⁺ + H₂O Zn(OH)₂ + H⁺

идет в значительно меньшей степени.

В. При гидролизе образуется сильное основание и слабая кислота:

K⁺ + A^- + H₂O K⁺ + HO^- + HA

или A^- + H₂O HA + HO^-,

pH>7.

Результатом гидролиза является образование слабодиссоциированной кислоты и повышение pH среды (среда щелочная).

При гидролизе солей, имеющих многовалентные анионы, образуются кислые соли:

Na₂CO₃ + H₂O NaHCO₃ + NaOH,

CO₃^2- + H₂O HCO₃^- + HO^-.

Г. При гидролизе образуются слабые основания и кислота:

K⁺ + A^- + H₂O KOH + HA,

CH₃COONH₄ + H₂O CH₃COOH + NH₄OH.

Уксусная кислота (CH₃COOH) и гидроксид аммония (NH₄OH) - слабые электролиты, поэтому глубина гидролиза в данном случае может быть выше, чем в ранее рассмотренных случаях (Б, В), но pH среды, определяющийся относительной силой образующихся кислоты и основания, близок к нейтральному.

Таким образом, увеличению степени гидролиза способствует разбавление раствора и повышение температуры. Снижение гидролиза может быть достигнуто повышением концентрации соли в растворе, снижением температуры и добавлением к раствору сильных кислот (Б) или оснований (В).

Примеры решения задач

Задача 4.1.

Найти количество воды и NaNO₃, необходимые для приготовления 2 л 22% раствора (d=1.14 г/мл).

Решение: масса 2 л раствора составляет 2 Ч 1.14 = 2.28 кг. Следовательно:

22 г NaNO3	-	100 г раствора,
х г	-	2280 г.

х = 501.6 г NaNO₃.

Отсюда масса воды m_H2O = 2280 - 501.6 = 1778.4 г.

Задача 4.2.

Рассчитать мольную долю, молярную, нормальную и моляльную концентрацию 78% раствора H₂SO₄ (d=1.70 кг/дм³).

Решение: прежде чем решать задачу, проанализируем ее исходные данные: по условиям 78 г H₂SO₄ (78/98=0.796 молей) содержится в 100 г (100/1.7=58.8мл) раствора, т.е. на 0.796 молей H₂SO₄ приходится (100-78)/18=1.222 моля H₂O.

Таким образом, мольная доля H₂SO₄:

= 0.796 / (0.796 + 1.222) = 0.3944.

Моляльная концентрация (количество молей вещества на 1000 г растворителя):

0.796 молей H2SO4	-	22 г H2O,
m	-	1000 г.

m = (0.796 Ч 1000)/22 = 36.18 моль/кг.

Молярная концентрация (количество молей вещества в 1 л раствора):

0.796 молей H2SO4	-	58.8 мл раствора,
М	-	1000 мл.

M = (0.796 Ч 1000)/58.8 = 13.5 моль/л.

Так как эквивалент H₂SO₄ составляет 1/2 моля, то

N = 2 Ч M = 2 Ч 13.5 = 27 моль/л.

Задача 4.3.

Какое количество 45.5% KOH (d=1.46 г/см³) потребуется для полной нейтрализации 0.5 л 2н серной кислоты?

Решение: в 0.5 л 2н H₂SO₄ содержится 1 эквивалент (0.5 моля) кислоты, следовательно, для ее нейтрализации потребуется 1 эквивалент (1 моль) щелочи.

В 100 г раствора KOH (100 : 1.46 = 68.5 мл) содержится 45.5 г (45.5/56 = 0.8125 моля) KOH. Составим пропорцию:

0.8125 моля KOH	-	685 мл раствора,
1 моль	-	х мл.

Таким образом, объем щелочи составляет

(68.5 Ч 1) : 0.8125 = 84.3 мл.

Задача 4.4.

Рассчитать давление пара раствора, содержащего 100 г сахарозы C₁₂H₂₂O₁₁ в 800 мл воды, если давление насыщенных паров воды при температуре 25°С составляет 3.167 кПа.

Решение: согласно закону Рауля давление пара над раствором составляет P₁ = N_H2OP_H2O, где P₁ - давление пара над раствором, P_H2O - давление пара над чистым растворителем, а N_H2O - мольная доля растворителя в растворе.

M_C12H22O11 = 342 г/моль

M_H2O = 18 г/моль

Следовательно: .

Поэтому давление паров воды над раствором

P₁ = N₁ Ч P₀ = 0.9935 Ч 3.167 = 3.146 кПа = 3146 Па.

Задача 4.5.

Найти температуру кипения и замерзания 20% раствора фенола (C₆H₅OH) в воде.

Решение: согласно закону Рауля Dt_кип = E Ч m,

Dt_зам = K Ч m,

где m - моляльная концентрация.

K_H2O=1.86°C,

E_H2O=0.52°C.

Найдем моляльную концентрацию раствора:

20 г фенола C6H5OH (m/M=20/94=0.2128 моля)		содержится в 80 мл воды,
x молей	-	в 1000 мл

Из этой пропорции: x = 0.2128 Ч 1000/80=2.66 моль/кг.

Следовательно: Dt_кип = 0.52 Ч 2.66 = 1.38°C,

Dt_зам = 1.86 Ч 2.66 = 4.95°C.

Таким образом, температура кипения раствора 101.38°C, а температура замерзания - 4.95°C.

Задача 4.6.

Найти осмотическое давление раствора, в 1.5 л которого содержится 300 г глюкозы (C₆H₁₂O₆), при 25°C.

Решение: согласно закону Вант-Гоффа P_осм = C Ч RT. Молярная концентрация раствора составляет (молекулярная масса глюкозы = 180):

C = 300 / 1.5 Ч 180 = 1.11 кмоль/м³.

Следовательно, P_осм = 1.11 Ч 8.314 Ч 298 = 2753 кПа.

Задача 4.7.

Найти процентную концентрацию раствора глюкозы, замерзающего при -5°C.

Решение: Dt_зам = K Ч m,

m = Dt_зам / K = 5/1.86 = 2.6882 моль/кг.

Таким образом, на 1000 г воды в растворе приходится 2.6882 Ч M_гл = 2.6882 Ч 180 = 483.9 г глюкозы.

Следовательно:

в (483.9 г глюкозы + 1000 г воды) т.е. в 1483.9 г раствора		содержится 483.9 г глюкозы,
100 г	-	x.

x = (483.9 Ч 100) / 1483.9 = 32.6%.

Задача 4.8.

Рассчитать объемы воды и этиленгликоля (C₂H₆O₂, M=62 г/моль, d=1.1088 г/см³), необходимые для получения 5 л антифриза (d=1.0713 кг/дм³), замерзающего при-40°С.

Решение: Dt = K Ч m,

m = Dt / K = 40/1.86 = 21.5 моль/кг.

Следовательно, на 1 кг воды в антифризе приходится 21.5 Ч 62 = 1333 г этиленгликоля.

Масса 5 л антифриза составляет 5 Ч 1.0713 = 5.356 кг. Следовательно:

в (1000 + 1333), т.е. в 2333 г антифриза		содержится 1333 г этиленгликоля,
5356 г	-	x.

x =(5356 Ч 1333) / 2333 = 3077 г = 3.077 кг,

масса воды 5356 - 3077 = 2279 г = 2.279 кг.

Таким образом, для получения 5 л антифриза потребуется 3.077 : 1.1088=2.775 л этилен-гликоля и 2.279 л воды.

Задача 4.9.

Раствор 1 г нитробензола в 65 г бензола застывает при 4.86°С. Температура кристаллизации бензола 5.5°С, К=5.12°С. Рассчитать молекулярную массу нитробензола.

Решение:

1 г нитробензола		растворен в 65 г бензола,
х	-	в 1000 г.

x = 1000/65 = 15.38 г.

Dt_кр = 5.5 - 4.86 = 0.64°С = K Ч m = 5.12 Ч m.

Отсюда m = 0.64 / 5.12 = 0.125 моль/кг.

Следовательно, 15.38 г нитробензола составляют 0.125 моля и M = 15.38/0.125 = 123 г/моль, что действительно соответствует формуле C₆H₅NO₂.

Задача 4.10.

Рассчитать кажущуюся степень диссоциации Na₂CO₃ в растворе, если при растворении 1.06 г его в 200 мл воды температура кипения повысилась на 0.062°С.

Решение:

Na₂CO₃ - электролит. По закону Рауля Dt_кип=iЧEЧm. Находим моляльную концентрацию раствора:

1.06г (1.06/106=0.01моля) Na2CO3		растворено в 200г H2O,
m	-	в 1000 г.

m = (0.01 Ч 1000) / 200 = 0.05 моль/кг.

Тогда изотонический коэффициент

.

.

Задача 4.11.

Рассчитать процентную концентрацию раствора KOH, если он замерзает при -0.519°С. Степень диссоциации щелочи в растворе 0.86.

Решение: ,

i = a + 1 = 0.86 + 1 = 1.86,

Dt=0-(-0.519)=0.519.

По закону Рауля Dt_зам = i Ч K Ч m, отсюда:

m = Dt_зам / i Ч K = 0.519 / (1.86 Ч 1.86) = 0.15 моль/кг.

Составим пропорцию:

0.15 моля, т.е. 0.15 Ч 56=8.4 г KOH		содержится в (1000+8.4) г раствора,
x	-	в 100 г.

x = (8.4 Ч 100) / 1008.4 = 0.833 г.

В 100 г раствора содержится 0.833 г KOH, т.е. процентная концентрация раствора равна 0.833%.

Задача 4.12.

Произведение растворимости AgBr составляет 5.3Ч10^-13 при 25°С. Вычислить растворимость соли (моль/л) при данной температуре.

Решение: обозначим растворимость AgBr за S моль/л. Тогда концентрации [Ag⁺]=[Br^-]=S моль/л. Следовательно, ПР = 5.3 Ч 10^-13 = S², и отсюда:

= 7.28 Ч 10^-7 моль/л.

Задача 4.13.

Возможно ли получение 0.001% раствора Ba₃(PO₄)₂ (м.м.=538) при комнатной температуре?

ПР_Ba3(PO4)2 = 6 Ч 10^-39.

Решение: если принять концентрацию соли за S моль/л, то [Ba²⁺]=3S, [PO₄^3-]=2S.

ПР = 6 Ч 10^-39 = [Ba²⁺]³ Ч [PO₄^3-]² = (3S)³ Ч (2S)² = 108 Ч S⁵,

моль/л

Таким образом, в 1 л раствора (плотность его можно принять за 1 г/см³) содержится

8.89 Ч 10^-9 Ч M = 8.89 Ч 10^-9 Ч 538 =4.783 Ч 10^-6 г.

Следовательно, концентрация насыщенного раствора не может быть больше чем

4.783 Ч 10-6	-	в 1000 г раствора,
x	-	в 100 г.

x = 4.783 Ч 10^-7%.

Задача 4.14.

Насыщенный раствор BaCrO₄ при некоторой температуре содержит 3.8 Ч 10^-4% соли. Рассчитать ПР_BaCrO4.

Решение: в 100 г раствора, плотность которого можно принять за 1 г/см³, содержится 3.8 Ч 10^-4 г соли. В 1 л раствора содержится 3.8 Ч 10^-3 г соли. То есть концентрация соли (м.м. BaCrO₄ =253) составит:

3.8 Ч 10^-3 / 253 = 1.5 Ч 10^-5 моль/л,

ПР = [Ba²⁺] Ч [CrO₄^2-]= (1.5 Ч 10^-5)² = 2.25 Ч 10^-10.

Задача 4.15.

Образуется ли осадок Ag₂SO₄, если к 0.01М раствору AgNO₃ добавить равный объем 0.25М раствора K₂SO₄? (ПР_Ag2SO4 = 2 Ч 10^-5)

Решение: при смешивании растворов концентрации растворов уменьшаются вдвое. Следовательно, [Ag⁺]=0.005 моль/л, [SO₄^2-]=0.125 моль/л. Тогда

[Ag⁺]² Ч [SO₄^2-]= (0.005)² Ч (0.125) = 3.125 Ч 10^-6.

3.125 Ч 10^-6 < ПР=2 Ч 10^-5, поэтому осадок не образуется.

Под химическими источниками тока (ХИТ) подразумевают устройства, в которых химическая энергия гетерогенных окислительно-восстановительных реакций, происходящих на поверхности электродов, может быть преобразована в электрическую энергию. Электрод, на поверхности которого происходит восстановление, называют катодом; электрод, на поверхности которого происходит окисление, называют анодом.

В основе работы таких устройств лежат явления, происходящие на границе раздела между металлом и раствором (расплавом) электролита, связанные с возникновением скачка потенциала (электродного потенциала). Электродный потенциал (j) зависит от природы металла, активности (концентрации) катионов металла в растворе (расплаве) и температуры. Электродный потенциал при стандартных условиях, т.е. при активности (концентрации) катионов металла 1 моль/л и температуре 298 К называют стандартным (j⁰). Стандартные электродные потенциалы, измеренные относительно эталонного водородного электрода, сведены в ряд напряжений. Потенциал водородного электрода (Pt, H₂/H₂SO₄) при стандартных условиях принят за нуль.

Электродные потенциалы любых окислительно-восстановительных систем (редокс-потенциалы) можно рассчитать по уравнению Нернста:

,

где j⁰ - стандартный потенциал (В), R - универсальная газовая постоянная (ДжЧмоль^-1ЧК^-1), n - число электронов, участвующих в окислительно-восстановительном процессе, Т - температура (К), F - постоянная Фарадея (Кл), [Ox] - концентрация окисленной формы, [Red] - концентрация восстановленной формы.

Подставив значения постоянных (R=8.314, T=298, F=96500) и приведя натуральные логарифмы к десятичным, получим

,

а для системы «металл-раствор соли металла»:

.

Движущей силой любой химической реакции является уменьшение свободной энергии Гиббса (DG), определяющей максимальную работу реакции. Максимальную работу ХИТ совершает в условиях равновесной реакции, которая возможна только при нулевой силе тока (I=0). В этих условиях

DG = -A_max = Q Ч U_max = Q Ч E,

где Q - количество электричества, U ‑ напряжение, E - электродвижущая сила ХИТ (ЭДС). То есть

DG = - n Ч F Ч E, или в стандартных условиях DG⁰ = - n Ч F Ч E ⁰.

Таким образом, ЭДС - разность потенциалов ХИТ, измеряемая компенсационным путем в условиях равновесных электродных процессов (I=0 А). Отсюда E > 0, поэтому расчет ЭДС гальванической системы ведут по схеме

E = j_катода - j_анода

(катод - электрод с бóльшим значением j, анод - с мéньшим). Например, для системы, состоящей из металлов А и В, опущенных в растворы их солей:

Me_A | соль Me_A || соль Me_B | Me_B

j_MeB > j_MeA; Me_A - анод, Me_B - катод.

Электродные процессы в ХИТ:

К: Me_Bⁿ⁺ + n e^- ѕ® Me_B,

А: Me_A - m e^- ѕ® Me_A^m+.

При этом количество электронов, участвующих в катодном и анодном процессах, должно быть одинаковым.

Электролизом называют совокупность процессов, происходящих при прохождении постоянного электрического тока через расплав или раствор электролита. Восстановительные (катодные) и окислительные (анодные) процессы происходят в соответствии с величиной электродного потенциала.

На катоде легче восстанавливаются частицы с бóльшим электродным потенциалом, на аноде легче окисляются частицы с мéньшим электродным потенциалом.

При определении процессов, протекающих на катоде при электролизе водных растворов, следует помнить:

1. Легко восстанавливаются ионы металлов с положительными значениями электродных потенциалов.

2. Ионы металлов с умеренно отрицательными значениями потенциалов (Zn²⁺, Fe²⁺, Cd²⁺, Ni²⁺ и другие) восстанавливаются одновременно с восстановлением ионов водорода (в кислой среде) или воды (в нейтральной или щелочной среде):

2H⁺ + 2e^- ѕ® H₂,

2H₂O + 2e^- ѕ® H₂ + 2OH^-.

3. Ионы металлов с высокоотрицательными значениями электродных потенциалов (j < -1.66 В, то есть от Li⁺ до Al³⁺ в ряду напряжений) ни при каких условиях не восстанавливаются при электролизе водных растворов.

При определении анодных процессов следует помнить:

1. При использовании металлических анодов (металлы с j⁰ < 0.8 В) окисляется материал анода:

Me⁰ - n e^- ѕ® Meⁿ⁺.

2. На инертных электродах при электролизе водных растворов легко окисляются одноатомные бескислородные анионы (кроме F^-).

3. Кислородсодержащие анионы при электролизе водных растворов практически не окисляются. В этих случаях идет окисление воды:

2H₂O - 4 e^- ѕ® O₂ + 4H⁺.

Количественно процессы электролиза описываются законом Фарадея: количество вещества, претерпевающего превращения при электролизе, пропорционально количеству прошедшего через электролит электричества.

m = k Ч Q или (для любых веществ),

(для газообразных веществ),

где m и V - масса и объем, I - сила тока, t - время, F - постоянная Фарадея (96500 Кл или 26.8 АЧчас), m_экв и V_экв - эквивалентная масса и объем данного вещества. При пропускании 96500 Кл или 26.8 АЧчаса электричества превращается 1 эквивалент вещества.

Отношение экв/F называют электрохимическим эквивалентом, т.е. оно характеризует количество вещества, превращающегося при пропускании 1 Кл (АЧс) или 1 АЧчаса электричества.

В условиях реального электролиза закон Фарадея в приведенной форме не выполняется, поэтому вводят поправку на выход по току:

,

где h -эмпирическая величина (в % или долях от 1), характеризующая неидеальность процесса:

%.

Для расчета расхода электроэнергии используют уравнение

W = Q Ч U,

где Q - количество электричества, U - напряжение в сети, В. При расчете нужно помнить, что 1 А Ч с Ч В=1Вт Ч с, поэтому

.

Примеры решения задач

Задача 5.1.

Рассчитать электродный потенциал системы Cu | CuSO₄ (0.01 М).

Решение: расчет проводим по уравнению

j = j⁰+(RT/nF) lg(C_Meⁿ⁺) = j⁰+(0.059/n) lg(C_Cu²⁺),

j⁰_Cu²⁺=0.338; n=2,

j = 0.338 + (0.059/2) lg(10^-2) = 0.279 В.

Задача 5.2.

Рассчитать электродный потенциал водородного электрода при pH=2, 7, 14.

Решение:

j = j⁰+(0.059/n) lg C_Meⁿ⁺ =

= j⁰_H⁺_/H + 0.059 lg C_H⁺=

= 0 + 0.059 lg C_H⁺ =

= -0.059 pH,

т.к. pH=-lg(C_H⁺).

Отсюда j_pH=2 = -2 Ч 0.059 = -0.118 В,

j_pH=7 = -7 Ч 0.059 = -0.413 В,

j_pH=14= -14 Ч 0.059 = -0.826 В.

Задача 5.3.

Рассчитать электродный потенциал системы Pt,H₂|H₂S (С=0.01 моль/л, К_Д(1)=6Ч10^-8).

Решение: для расчета потенциала этого водородного электрода необходимо найти концентрацию ионов водорода в растворе (или pH). H₂S - слабый электролит:

H₂S H⁺ + HS^-.

.

Следовательно, [H⁺] = aC = 2.45 Ч 10^-3 Ч 0.01 = 2.45 Ч 10^-5.

pH = - lg C_H⁺ = - lg 2.45 Ч 10^-5 = 4.61;

j = -0.059 pH = -0.059 Ч 4.61 = -0.272 В.

Задача 5.4.

Рассчитать потенциал водородного электрода Pt,H₂|NaOH (С=0.01 моль/л).

Решение: для расчета pH раствора используем ионное произведение воды:

NaOH Na⁺ + HO^-,

[HO^-] = [NaOH] = 0.1 М.

Следовательно, [H⁺]=K_H2O/[HO^-]=10^-14/0.1=10^-13.

pH=-lg(C_H⁺) = 13;

j = -0.059 pH = -0.059 Ч 13 = -0.767 В.

Задача 5.5.

Определить ЭДС гальванического элемента

Zn | ZnSO₄ || Fe(NO₃)₃ | Fe

0.01 моль/л 0.1 моль/л

и привести схему электродных процессов.

Решение:

j_Zn|Zn2+ = -0.763 + lg(0.01) Ч 0.059/2 = -0.822 В,

j_Fe|Fe3+ = -0.037 + lg(0.1) Ч 0.059/3 = -0.057 В.

j_Fe|Fe3+ > j_Zn|Zn2+ , следовательно, железный электрод является катодом, а цинковый - анодом.

К: 2Fe³⁺ + 6e ѕ® 2Fe.

А: 3Zn - 6e ѕ® 3Zn²⁺.

E = j_К - j_А = -0.057 - (-0.822) = 0.765 В.

Задача 5.6.

Определить ЭДС концентрационного элемента и привести схему электродных процессов:

Cr | Cr₂SO4 || CrCl₂ | Cr

 0.1 моль/л 0.001 моль/л 

Решение:

j₁ = -0.91 + lg(0.1) Ч 0.059/2 = -0.9395 В,

j₂ = -0.91 + lg(0.01) Ч 0.059/2 = -0.9985 В.

Следовательно, катодом является электрод , а анодом - электрод .

К (электрод ): Cr²⁺+ 2e ѕ® Cr.

А (электрод ): Cr - 2e ѕ® Cr²⁺.

E = j₁ - j₂ = 0.059 В.

Задача 5.7.

Определить ЭДС и написать электродные процессы в гальваническом элементе:

H₂(Pt) | HCl || NaOH | (Pt)H₂

0.1 моль/л 0.01 моль/л

Решение:

j_H|H+ = -0.059 pH.

В сильной кислоте [H⁺]=0.1, т.е. pH=1, следовательно, j_H|H+ = -0.059 В.

В щелочи [HO^-]=0.01 м/л, значит, [H⁺]= 10^-14/0.01 = 10^-12 и pH=12.

Следовательно, потенциал этого электрода:

j = -0.059 Ч 12 = -0.708 В.

Отсюда:

E = -0.059 - (-0.708) = 0.649 В.

К: 2H⁺+ 2e ѕ® H₂ (электрод с HCl).

А: H₂ - 2e ѕ® 2H⁺ (электрод с NaOH).

Задача 5.8.

Найти концентрацию (моль/л) FeCl₂ в гальваническом элементе:

Mn | MnSO₄ || FeCl₂ | Fe,

0.01 моль/л x моль/л

если ЭДС элемента составляет 0.7215 В.

Решение:

j_Mn|Mn2+ = -1.192 + lg(0.01) Ч 0.059/2 = -1.251 В.

0.7215 = j_Fe|Fe2+ - (-1.251), значит j_Fe|Fe2+=-0.5295 В.

j_Fe|Fe2+ = -0.441 + lg(x) Ч 0.059/2 = -0.5295 В.

Следовательно, lg x = (-0.5295+0.441)/0.0295 = -3.

Поэтому [FeCl₂] = 0.001 моль/л.

Задача 5.9.

Определить количество алюминия, которое можно получить при электролизе Al₂O₃ током 25А в течение 24 часов при выходе по току 88%.

Решение: учитывая, что при пропускании 26.8 АЧчаса (1F) электричества можно получить 1 экв. алюминия (9 г), составим пропорцию:

26.8 А Ч ч	-	9 г Al,
25 А Ч 24часа	-	х г Al,

откуда х = 25 Ч 24 Ч 9 / 26.8 = 201.5 г.

Однако из-за 88% выхода по току практически получаемое количество Al составит

m_Al = 201.5 Ч 0.88 = 177.3 г.

Задача 5.10.

Определить время, которое потребуется для получения 100 л водорода (н.у.) электролизом раствора NaOH током 3А при выходе по току 75%.

Решение: 1 F (26.8 А Ч ч) расходуется на получение 1 экв. водорода (11.2 л), следовательно:

26.8 А Ч ч	-	11.2 л,
3 А Ч t	-	100,

откуда t = (26.8 × 100)/(3 × 11.2) = 79.8 часа.

Практически же потребуется из-за 75% выхода по току

t_пр = t / 0.75 = 106.3 часа.

Задача 5.11.

Ток силой 10 А пропускали через 0.5 кг 5%-го раствора NaOH. Через сколько часов концентрация раствора увеличится вдвое? Выход по току считать 100%.

Решение: при электролизе водного раствора щелочи происходит разложение воды с выделением водорода на катоде и кислорода на аноде. Следовательно, концентрация щелочи по ходу электролиза возрастает. Количество NaOH в растворе постоянно и равно 0.05 × 500=25 г. Обозначим убыль воды за х грамм. Тогда масса раствора составит (500-х) г. Следовательно, в 10% растворе щелочи:

25 / (500-х) = 0.1

25 = 50 - 0.1 × х

0.1 × х = 25

х = 250 г.

То есть чтобы вдвое увеличить концентрацию щелочи в растворе, необходимо разложить 250 г воды.

Найдем время t, за которое пройдет разложение этого количества воды из пропорции

26.8 А Ч ч	-	9 г (1 экв.) воды,
10 А Ч t	-	250.

Отсюда t = (26.8 × 250)/(10 × 9) = 74.4 часа.

Задача 5.12.

Определить объем кислорода (н.у.), который можно получить, затратив 100 кВт × ч электроэнергии при напряжении в сети 10 В и выходе по току 79%.

Решение: известно, что количество электроэнергии (W) и количество электричества (Q) связаны уравнением:

W = Q × U

100 кВт × ч = 100 000 Вт × ч = Q × 10 В

Q = 100 000 / 10 = 10 000 А × час

Отсюда:

26.8 А Ч ч (1 F)	-	5.6 л (1 экв.) кислорода (н.у.)
10 000 А Ч ч	-	х л

Из этой пропорции находим х = (10000 × 5.6)/26.8 = 2089.6 л.

С учетом выхода по току количество кислорода, которое можно получить при этих условиях,

V_кисл = 2086.6 × 0.79 = 1650.7 л.

Задача 5.13.

Укажите наиболее коррозионно-опасный контакт металлов:

Cu/Fe, Cr/Co, Mg/Ni

Решение: в одинаковых условиях скорость коррозии пропорциональна разности потенциалов металлов в контакте (ЭДС элемента).

	Cu/Fe		Cr/Co		Mg/Ni
j0, В	0.338	- 0.441	- 0.91	- 0.234	- 2.37	- 0.25
E, В	0.779		0.676		2.12

Следовательно, наиболее коррозионно-опасным является контакт Mg/Ni.

Задача 5.14.

Укажите катодные (опасные) и анодные (неопасные) покрытия железа:

Sn/Fe, Cu/ Fe, Cr/ Fe

Решение: катодным для железа является покрытие металлом, имеющим больший электродный потенциал, т.е. в гальванической паре с железом металл покрытия должен выполнять катодные функции (анод - железо). Такие покрытия опасны - при повреждении покрытия развивается подповерхностная коррозия (разрушение железа под покрытием). Анодным является покрытие железа более активным металлом, имеющим более низкий электродный потенциал. Металл такого покрытия выполняет роль анода. В приведенных примерах:

Sn/Fe		Cu/Fe		Cr/Fe
- 0.14	- 0.441	+ 0.338	- 0.441	- 0.91	- 0.441

Покрытия оловом и медью являются катодными, хромом - анодным.

Задача 5.15.

Напишите электродные процессы при коррозии для контактов:

Fe/Zn в HCl_разб,

Fe/Sn во влажном воздухе,

Cu/Zn в серной кислоте.

Решение:

1. В паре Fe_-0.441/Zn_-0.763 анодом является цинк, следовательно:

А:	Zn - 2e	¾®	Zn2+,
К:	2H+ + 2e	¾®	H2.

2. В паре Fe_-0.441/Sn_-0.14 анодом является железо, следовательно:

А:	2Fe - 4e	¾®	2Fe2+,
К:	O2 + 2H2O + 4e	¾®	4HO-.

3. В паре Cu_+0.338/Zn_-0.763 анодом является цинк, следовательно:

А:	2Zn - 4e	¾®	2Zn2+,
К:	O2 + 4H+ + 4e	¾®	2H2O.

Задачи и упражнения

по общей химии

Сергей Петрович Коршунов

Валентина Михайловна Казанцева

Редактор Н.А. Фомичева

Подписано в печать 5.10.98. Печать оперативная. Усл. п.л. 2,5. Уч.-изд. л. 2,3. Тираж экз. Заказ № .

Тольяттинский политехнический институт

Тольятти, ул. Белорусская, 14

38