24. Основные положения мкт. Идеальный газ. Основное уравнение мкт идеального газа. Молекулярно-кинетическое истолкование температуры.

Молекулярно-кинетическая теория - теория, объясняющая тепловые явления в макроскопических телах и свойства этих тел на основе их молекулярного строения. Основные положения молекулярно-кинетической теории: 1)вещество состоит из частиц - молекул и атомов, разделенных промежутками. 2)эти частицы хаотически движутся. 3)частицы взаимодействуют друг с другом. Идеальный газ - это упрощенная модель газа, в которой: 1)молекулы газа считаются материальными точками. 2) молекулы не взаимодействуют между собой. 3)молекулы, соударяясь с преградами, испытывают упругие взаимодействия.

, откуда . Основное уравнение МКТ

Эту зависимость часто рассматривают как молекулярно-кинетическое толкование температуры — температура есть мера кинетической энергии молекул.

25. Закон равномерного распределения энергии по степеням свободы. Средняя кинетическая энергия теплового движения молекул идеального газа. Внутренняя энергия идеального газа.

Число степеней свободы – это число независимых величин с помощью которых может быть задано положение системы. (1 атом =3 ст., 2 атома =5ст. 3 атома=6ст.) Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная КТ/2 , а на каждую колебательную – КТ. Средняя энергия молекулы _. Внутренняя энергия для 1 моля _. Для массы m газа .Средняя кинетическая энергия молекул газа (в расчете на одну молекулу) определяется выражением:Где бv ²с – среднее значение квадрата скорости молекул, m – масса молекулы. Внутренняя энергия идеального газа зависит только от температуры U=BT где В- коэф. пропорциональности. Внутренняя энергия для 1 моля для массы m газаВнутренняя энергия одного моля газаВн. Энергия произвольной массы газа

26. Закон распределения молекул газа по скоростям. Наиболее вероятная, ср. арифметическая и среднеквадратичная скорости молекул. Распределение молекул газа по модулю скоростей называется распределением Максвелла (1860 г.). Дж. Максвелл вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. Распределение Максвелла может быть получено при помощи статистической механики(см. происхождениестатсуммы).. Наиболее вероятная скорость,— вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению. Чтобы найти её, необходимо вычислить, приравнять её нулю и решить относительно.

.

Среднеквадратичная скорость. Подставляя и интегрируя, мы получим

Средняя скорость. Подставляя и интегрируя, мы получим

27. Барометрическая формула. Закон Больцмана распределения молекул во внешнем потенциальном поле.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуруT и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного паденияg одинаково), барометрическая формула имеет следующий вид:

где p — давление газа в слое, расположенном на высоте h, p₀ — давление на нулевом уровне (h = h₀), M — молярная масса газа, R — газовая постоянная,T — абсолютная температура.

Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул)в условияхтермодинамического равновесия; открытоЛ. Больцманомв1868—1871..- число молекул в единице объема в том месте где потенциальная энергия молекулы равна нулю.n – число молекул в единице объема, соответствующая тем точкам пространства где потенциальная энергия молекулы равна

28. Термодинамические параметры. Равновесные состояния и процессы. Уравнене состояния идеального газа. Термодинамические диаграммы равновесных термодинамических процессов. Изопроцессы идеального газа.

Термодинамические параметры - температура, плотность, давление, объем, удельное электрическое сопротивление и другие физические величины: 1)однозначно определяющие термодинамическое состояние системы; 2)не учитывающие молекулярное строение тел; 3) описывающие их макроскопическое строение. Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близкихравновесных термодинамических состояний. Равновесный тепловой процесс называетсяобратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений. Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими.Равновесные и неравновесные состояния. Равновесным является такое состояние изолированной системы, в которое она переходит по истечении, строго говоря, бесконечно большого промежутка времени. Практически равновесие достигается за конечное время (время релаксации), которое зависит от природы тел, их взаимодействий, а также и от характера исходного неравновесного состояния. Если система находится в состоянии равновесия, то в равновесии находятся и отдельные её макроскопические части. При неизменных внешних условиях такое состояние не меняется со временем. Следует подчеркнуть, что неизменность во времени не является достаточным признаком равновесности состояния. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением,молярным объёмомиабсолютной температуройидеального газа. Уравнение имеет вид:.Изопроцессы — термодинамические процессы, во время которых масса и ещё одна из физических величин — параметров состояния:давление,объёмилитемпература— остаётся неизменной. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — адиабатический.. Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называютсяизобара,изохора,изотермаиадиабатасоответственно. Изопроцессы являются частными случаямиполитропного процесса.Изобарный процесс (от греч. "барос" — вес, тяжесть) — процесс изменения состояния термодинамической системы при постоянном давлении.P=const => V/t=const. Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме. Для идеальных газов изохорический процесс описывается законом Шарля. V=const => P/t=const. Изотермический процесс (от греч. "термос" — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре t=const => P*V=const. Адиабатический процесс — процесс изменения состояния термодинамической системы при постоянной энтропии S=const => pV^k = const.

29. Адиабатный процесс. Уравнение Пуассона. Показатель адиабаты.

Адиабатический процесс — термодинамический процессв макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. Формула адиабатического процесса-ΔU = A. Для идеальных газовадиабата имеет простейший вид и определяется уравнением:pV^k = const. k = C_p / C_v — показатель адиабаты. C_p и C_v — теплоёмкостигаза соответственно при постоянном давлении и постоянном объёме. С учётомуравнения состояния идеального газауравнение адиабаты может быть преобразовано к виду:Т^kp^1—k = const , где T — абсолютная температурагаза. Или к виду:TV^k—1 = const. Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессыобратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатический процесс необратим.Уравне́ние Пуассо́на — эллиптическоедифференциальное уравнение в частных производных, которое, описывает: 1)электростатическое поле2)стационарное поле температуры 3)поле давления 4)поле потенциала скорости в гидродинамике. Это уравнение имеет вид:. гдеΔ — оператор Лапласаилилапласиан, аf — действительнаяиликомплекснаяфункцияна некотороммногообразии.

30. Теплота и работа как функции процесса. Внутренняя энергия как функция состояния. Первое начало термодинамики и его применение к изопроцессам идеального газа.

Теплота - функцияпроцесса:количествосообщенной телу теплоты зависит не только от того, каковы начальное и конечное состояния тела, но также от вида процесса. Элементарноеколичествотеплоты dQ=CdT, где C -теплоемкостьтела в рассматриваемом процессе, dT - малое изменение температуры тела.Первое начало термодинамики — одно из основных положений термодинамики, являющееся, по существу,законом сохранения энергиив применении к термодинамическим процессам. Первое начало термодинамики было сформулировано в серединеXIX векав результате работЮ. Р. Майера,ДжоуляиГ. Гельмгольца. Первое начало термодинамики часто формулируют как невозможность существованиявечного двигателя1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника.

1) Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил.

2) Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе и не зависит от способа, которым осуществляется этот переход.

а) при изобарном процессеб) при изохорном процессе (A=0)в) при изотермическом процессе(ΔU = 0)

Вну́тренняя эне́ргия тела (обозначается как E или U) — полная энергия этого тела за вычетом кинетической энергиитела как целого ипотенциальной энергиитела во внешнем поле сил. Следовательно, внутренняя энергия складывается из кинетической энергиихаотическогодвижениямолекул, потенциальной энергии взаимодействия между ними и внутримолекулярной энергии. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

30. Теплота и работа как функции процесса. Внутренняя энергия как функция состояния. Первое начало термодинамики и его применение к изопроцессам идеального газа.

Внутр энерг U- энерг хаотич(теплов) движ макрочастиц сист (молекул, атомов, эл-нов, ядер и т.д.) и энергия взаимдейств этих частиц. При переход из одного сост в др, изменен внутр энерг опред тольк разностью знач внутр энерг этих сост и не завис от пути перехода. Сущ 2 формы передачи энерг от одних тел к др:работа и тепол.энерг мех движ может превр в энерг тепл движ и наоборот.

Теплота, сообщ сист расх на изменение ее внутр энерг и на соверш ею работы против внеш сил. Q=dU+A.если сист периодич возвр в первонач сост, то измее внут энерг ∆U=0, тогда A=Q. Работа газа при изменен его объема: A=интеграл отV1 до V2 pdV

Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и на совершение телом работы: Q=∆U+A – это и есть первое начало термодинамики, или закон сохранения энергии в термодинамике.

Первый закон (первое начало) термодинамики можно сформулировать так:

«Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщённого системе, в сумме с изменением энергии, связанной с количеством вещества N при химическом потенциале μ, и работы A', совершённой над системой внешними силами и полями, за вычетом работы A, совершённой самой системой против внешних сил» :

ΔU = Q − A + μΔN + A'.

Для элементарного количества теплоты δQ, элементарной работы δA и малого приращения (полного дифференциала) dU внутренней энергии первый закон термодинамики имеет вид:

dU = δQ − δA + μdN + δA'.

31. Вычисление работы, совершаемой идеальным газом в различных процессах.

Адиаботическим наз-ся процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Из первого начала термодинамики следует что δA=- δQ т.е. внешняя работа совершеться за счет внутреней

При изобарном процессе работа газа при увелечени объема от V1 до V2 равна A=интеграл(от V1 до V2) pdV=p(V1-V2).

При изохорном процессе гах не совершает работ над внешними телами т.е δA= pdV=0

Из первого начала термодинамики для изотермического процесса следует, что δA= δQ т.е все кол-во теплоты, сообщяемое газу расходуеться на совершение им работы против внешшних сил.

32. Теплоемкость. Классическая МКТ теплоемкости идеального газа и ее ограниченность.

Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT: C= δQ/ δТ

Единица измерения теплоёмкости в системе СИ — Дж/К.

Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).

Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).

Классическая молекулярно-кинетическая теория газов рассматривает идеальный газ как совокупность абсолютно жестких молекул, между которыми отсутствуют силы взаимодействия и каждая молекула обладает лишь энергией поступательного и вращательного движений, а сами молекулы рассматриваются как материальные точки.

Одноатомный газ имеет только три степени свободы поступательного движения (i=3). Молекула двухатомного газа кроме поступательного движения может совершать и вращательное движение вокруг общего центра тяжести, который находится на линии, соединяющей оба атома. Такая молекула двухатомного газа имеет пять степеней свободы (i=5), из них три степени свободы поступательного движения и две степени свободы вращательного движения.

33. Обратимые и необратимые термодинамические процессы. Второе начало термодинамики в формулировках Клаузиуса и Томсона.

ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ, пути изменения состояния термодинамич. системы. Процесс наз. обратимым, если он допускает возвращение рассматриваемой системы из конечного состояния в исходное через ту же последовательность промежут. состояний, что и в прямом процессе, но проходимую в обратном порядке. При этом в исходное состояние возвращается не только система, но и среда. Обратимый процесс возможен, если и в системе, и в окружающей среде он протекает равновесно. При этом предполагается, что равновесие существует между отдельными частями рассматриваемой системы и на границе с окружающей средой. Обратимый процесс - идеализир. случай, достижимый лишь при бесконечно медленном изменении термодинамич. параметров. Скорость установления равновесия должна быть больше, чем скорость рассматриваемого процесса. Если невозможно найти способ вернуть и систему, и тела в окружающей среде в исходное состояние, процесс изменения состояния системы наз. необратимым. Необратимые процессы могут протекать самопроизвольно только в одном направлении; таковы диффузия. теплопроводность. вязкое течение и др.

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса).

Постулат Томсона: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

34. Тепловые машины. Термический КПД теплового двигателя. Цикл Карно. Теорема Карно.

Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий рабо­ту за счет охлаждения одного источника теплоты, — невозможен.

Принцип действия теплового двигателя. От термостата с более высокой температурой Т₁, т.е. нагревателя, за цикл отнимается кол-во теплоты Q₁, а термостату с более низкой температурой Т₂, т.е. холодильнику, за цикл передается кол-во теплоты Q₂, при этом совершается работа А = Q₁ – Q₂.

Чтобы термический коэффициент полезного действия теплового двигателя был равен 1, необходимо выполнение условия Q₂ = 0, т. е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Французский физик и инженер Карно показал, что для работы теплового двигателя необ­ходимо не менее двух источников теплоты с различными температурами, иначе это противоречило бы второму началу термодинамики.

Процесс, обратный происходящему в тепловом двигателе, используется в холо­дильной машине. Системой за цикл от термостата с более низкой температурой Т₂ отнимается количество теплоты Q₂ и от­дается термостату с более высокой температурой Т₁ количество теплоты Q₁. Для кругового процесса Q=A, но, по условию, Q = Q₂ – Q₁ < 0, поэтому А<0 и Q₂ – Q₁ = –А, или Q₁ = Q₂ + A, т. е. количество теплоты Q₁, отданное системой источнику теплоты при более высокой температуре T₁ больше количества теплоты Q₂, полученного от источника теплоты при более низкой температуре T₂, на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это - Второе Начало Термодинамики в формулировке Клаузиуса.

Основываясь на втором начале термодинамики, Карно вывел теорему, носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих оди­наковые температуры нагревателей (T₁) и холодильников (T₂), наибольшим к. п. д. обладают обратимые машины; при этом к. п. д. обратимых машин, работающих при одинаковых температурах нагревателей (T₁) и холодильников (T₂), равны друг другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника.

Карно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат. Его называют циклом Карно. Прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.

Изотермические расширение и сжатие в Цикле Карно заданы соответственно кривыми 1—2 и 3—4, а адиабатические расширение и сжатие — кривы­ми 2—3 и 4—1. При изотермическом процессе U=const, кол-во теплоты Q₁, полученное газом от нагревателя, равно работе расширения А₁₂, совершаемой газом при переходе из состояния 1 в состояние 2:

(59.1)

При адиабатическом расширении 2—3 теплообмен с окружающей средой отсутствует и работа расширения А₂₃ совершается за счет изменения внутренней энергии:

Количество теплоты Q₂, отданное газом холодильнику при изотермическом сжатии, равно работе сжатия А₃₄:

(59.2)

Работа адиабатического сжатия

Работа, совершаемая в результате кругового процесса,

К.П.Д. цикла Карно

Для адиабат 2—3 и 4—1

откуда

(59.3)

(59.4)

т. е. для цикла Карно к. п. д. действительно определяется только температурами нагревателя и холодильника.

35. Энтропия и ее свойства. Статистическое истолкование второго начала термодинамики. Связь энтропии с вероятностью состояния.

Энтропи́я (от греч. ἐντροπία — поворот, превращение) — понятие, впервые введённое в термодинамике для определения меры необратимого рассеивания энергии. Термин широко применяется и в других областях знания: в статистической физике — как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации как мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).

Свойства энтропии:

1. Энтропия изолированной системы при протекании необратимого процесса возрастает. Действительно, изолированная (т. е. предоставленная самой себе) система переходит из менее вероятных в более вероятные состояния, что сопровождается ростом величины S.

2. Энтропия системы, находящейся в равновесном состоянии, максимальна.

Итак, при протекании в изолированной системе необратимого процесса энтропия возрастает, т. е. выполняется соотношение dS > 0.

Статистическое истолкование второго начала термодинамики

Понятие о термодинамической вероятности состояния системы. Статистическая формулировка второго начала термодинамики. Уравнение Больцмана-Планка, связывающее энтропию и термодинамическую вероятность. Распределение частиц идеального газа по энергиям в состоянии равновесия. Понятие суммы состояний.

36. Общая характеристика явлений переноса. Поток и плотность потока. Феноменологическое явление переноса.

Плотность потока — общий базовый физический термин, который используется в следующих областях: в случае явлений переноса (теплообмене, массообмене и гидроаэродинамике), плотность потока определяют как вектор, который проходит через единицу площади за единицу времени. Допустим, вдоль оси х распространяется продольная плоская волна. Выделим объём с основанием S0 и высотой Δх. Смещения S частиц с разными координатами х в каждый момент времени t различные: координата х — смещение S, координата х + Δх — смещение S + Δ S.

в электродинамике, поток обычно определяют, как интеграл векторного количества по конечной поверхности.

В термодинамически неравновесн сист возник особ необратим проц-сы, назыв явлениями переноса, в результ котор происх пространств перенос энерг, массы,импульса.К явлереноса относ теплопровод(перенос энерг),дифуз(перенос массы) и внутр трен(перенос импульса).перенос энерг в форме теплоты подч зак Фурье:

Je= - λdT/dx, явл дифуз-зак Фика Jm= -D*

*dp/dx, и внутр трен - зак Ньютона. F=η* *dv/dx по модулю*S, где

Je-плотность теплового потока

λ – теплопроводность

dT/dx- град темп

Jm-плотность потока массы.

D-диффузия

dp/dx- градиент плотности.

η- динамическая вязкость

dv/dx- градиент скорости

S- площадь, на которую действ сила F.

37. Диффузия. Закон Фика.

Диффузия. Явление диффузии заключается в том, что происходит самопроиз­вольное проникновение и перемешивание частиц двух соприкасающихся газов, жид­костей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте.

Явление диффузии для химически однородного газа подчиняется закону Фука:

(48.3)

где j_m — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), d/dx — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки j_m и d/dx противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинети­ческой теории газов,

38. Внутреннее трение (вязкость). Закон Ньютона для вязкого трения.

Механизм возникновения внутреннего трения меж­ду параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:

(48.5)

где  — динамическая вязкость (вязкость), dv/dx — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению дви­жения слоев, S — площадь, на которую действует сила F.

Взаимодействие двух слоев согласно второму закону Ньютона можно рассматри­вать как процесс, при котором от одного слоя к другому в ед времени передается импульс, по модулю равный действующей силе. Тогда выражение (48.5) можно пред­ставить в виде

(48.6)

где j_p — плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х, 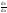— градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки j_р и 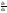противоположны).

Динамическая вязкость  численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле

(48.7)

Из сопоставления формул (48.1), (48.3) и (48.6), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были установлены задолго до того, как они были обоснованы и выведены из молекулярно-кинетической теории, позволившей установить, что внешнее сходство их математи­ческих выражений обусловлено общностью лежащего в основе явлений теплопровод­ности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.

Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетического смысла коэффициентов , D и . Выражения для коэффициентов переноса выводятся из кинетической теории.

39. Явление теплопроводности. Закон Фурье

Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных сто­лкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.

Перенос энергии в форме теплоты подчиняется закону Фурье:

(48.1)

где j_E — плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х,  — теплопроводность, 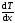— градиент температуры, равный скорости изменения температуры на единицу длиных в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки j_E и – противоположны). Теплопроводность численно равна плотности теплового потока при градиенте температуры, равном единице.

Можно показать, что

(48.2)

где с_V — удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме),  — плотность газа, <v> — средняя скорость теплового движения молекул, <l> — средняя длина сво­бодного пробега.

40. Среднее число столкновений и средняя длинна свободного пробега. Эффективный диаметр молекулы.

Молекулыгаза, находясь в состоянии хаотического движения, непрерывно сталкивают­ся друг с другом. Между двумя последовательными столкновениями молекулы прохо­дят некоторый путьl, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул <l>.

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 68). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры).

Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости <v>, и если <z> — среднее число столкновений, испытываемых одной молеку­лой газа за 1 с, то средняя длина свободного пробега

Для определения <z> представим себе молекулу в виде шарика диаметром d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра радиусом d (рис. 69).

Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра:

где п — концентрация молекул, V = d² <v> <v> — средняя скорость молекулы или путь, пройденным ею за 1 с). Таким образом, среднее число столкновений

Расчеты показывают, что при учете движения других молекул

Тогда средняя длина свободного пробега

т. е. <l> обратно пропорциональна концентрации n молекул. С другой стороны, из (42.6) следует, что при постоянной температуре n пропорциональна давлению р. Следовательно,

42. Электрический заряд и его свойства. Закон сохранения электрического заряда. Взаимодействие эл. Зарядов. Электрическое поле. Напряженность Эл. Поля.

Эл. заряд – это физ. величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.Эл. заряд обычно обозначается буквами q или Q.Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:1)Существует два рода эл. зарядов, условно названных положительными и отрицательными.2)Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.3)Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.4)Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной: q1 + q2 + q3 + ... +qn = const. Закон сохранения эл. заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду e. e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:

Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом и Однако, в свободном состоянии кварки до сих пор наблюдать не удалось. Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними: F=(kq₁q₂)/r². Силы взаимодействия подчиняются третьему закону Ньютона: F=-F. Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой. Коэффициент k в системе СИ обычно записывают в виде:k= 1/4πέ₀. Где έ₀ =8,85*10^-12. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство эл.поля – действие на эл. заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов.Для количественного определения эл.поля вводится силовая характеристика напр-ть электрического поля.Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда: E=F/q;

43. Электростатическое поле. Напряженность и потенциал поля точечного заряда. Принцип суперпозиции электростатических полей.

Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности: Это свойство эл. поля означает, что поле подчиняется принципу суперпозиции.В соответствии с законом Кулона, напр-сть электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:E=(k*Q)/r². Это поле называется кулоновским. В кулоновском поле направление вектора E зависит от знака заряда Q: если Q > 0, то вектор E направлен по радиусу от заряда, если Q < 0, то вектор E направлен к заряду. Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора E в каждой точке совпадало с направлением касательной к силовой линии.При изображении электрического поля с помощью силовых линий, их густота должна быть пропорциональна модулю вектора напряженности поля. Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рис. 1.2.2. Так как электростатическое поле, создаваемое любой системой зарядов, может быть представлено в виде суперпозиции кулоновских полей точечных зарядов, изображенные поля можно рассматривать как элементарные структурные единицы («кирпичики») любого электростатического поля. Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r от заряда Q к точке наблюдения. Тогда при Q > 0 вектор E параллелен, а при Q < 0 вектор E антипараллелен r. Следовательно, можно записать:

44. Поток вектора напряженности Е. Теорема Гаусса и ее применение для расчета напряженности электростатического поля.

Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Понятие потока вектора E аналогично понятию потока вектора скорости V при течении несжимаемой жидкости. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора E на площадь ΔS и на косинус угла α между вектором E и нормалью n к площадке называется элементарным потоком вектора напряженности через площадку ΔS: ΔΦ = EΔS cos α = EnΔS, где En – модуль нормальной составляющей поля E. Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки ΔΦi поля E через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора E, через замкнутую поверхность S. . Теорема Гаусса утверждает:Поток вектора напряженности электростатического поляE через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0. .Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиусаR. Эта задача имеет осевую симметрию. Из соображений симметрии, электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов. При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает: . гдеτ – заряд единицы длины цилиндра. Отсюда: -определение поля равномерно заряженной нити.

46. Электрический диполь и его поле. Электрический момент диполя. Диполь в однородном и неоднородном эл. Полях.

Диполь (от ди... и греч. pólos — полюс) электрический, совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Основной характеристикой электрического Д. является его дипольный момент — вектор, направленный от отрицательного заряда к положительному (рис. 1) и численно равный произведению заряда е на расстояние l между зарядами: р = el. Дипольный момент определяет электрическое поле Д. на большом расстоянии R от Д. (R»l), а также воздействие на Д. внешнего электрического поля. Вдали от Д. его электрическое поле Е убывает с расстоянием как 1/R3, т. е. быстрее, чем поле точечного заряда (~ 1/R2). Компоненты напряжённости поля Е вдоль оси Д. (Ep) и в направлении, перпендикулярном к р (E┴), пропорциональны дипольному моменту и в системе единиц СГС (Гаусса) равны: . где J — угол между р и радиусом-вектором R точки пространства, в которой измеряется поле Д.; полная напряжённость. Т. о., на оси Д. при J = 0 напряжённость поля вдвое больше, чем при J = 90°; при обоих этих углах оно имеет только компоненту Ep, причём при J = 0 её направление параллельно р, а при J = 90° — антипараллельно. Действие внешнего электрического поля на Д. также пропорционально величине его дипольного момента. Однородное поле создаёт вращающий момент М = pE sina (a — угол между вектором напряжённости внешнего электрического поля Е и дипольным моментом р), стремящийся повернуть Д. так, чтобы его дипольный момент был направлен по полю. В неоднородном электрическом поле на Д., кроме вращающего момента, действует также сила, стремящаяся втянуть Д. в область более сильного поля. Электрическое поле любой нейтральной в целом системы на расстояниях, значительно больших её размеров, приближённо совпадает с полем эквивалентного Д. — электрического Д. с таким же дипольным моментом, как и у системы зарядов (т. е. поле на больших расстояниях от системы нечувствительно к деталям распределения зарядов). Поэтому во многих случаях электрический Д. является хорошим приближением для описания такой системы на больших по сравнению с её размерами расстояниях. Например, молекулы многих веществ можно приближённо рассматривать как электрический Д. (в простейшем случае это молекулы из двух ионов с зарядами противоположных знаков); атомы и молекулы во внешнем электрическом поле, несколько раздвигающем их положительные и отрицательные заряды, приобретают индуцированный (наведённый полем) дипольный момент и становятся микроскопическими Д. Эл. Д. с изменяющимся во времени дипольным моментом (вследствие изменения его длины l или зарядов e) является источником электромагнитного излучения.

45. Работа по перемещению заряда в эл.поле. Потенциал и разность потенциалов. Связь напряженности и потенциала. Теорема о циркуляции вектора напряженности электростатического поля.

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.Следствием независимости работы от формы траектории является следующее утверждение:Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.Силовые поля, обладающие этим свойством, называют потенциальными или консервативными. Работа ΔA кулоновских сил на этом перемещении равна: . Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить:. Полученный результат не зависит от формы траектории. Если электростатическое поле создается совокупностью точечных зарядов Qi, то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ Ai кулоновских полей точечных зарядов:Так как каждый член суммы Ai не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка, и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.Потенциальная энергия заряда q, помещенного в любую точку пространства, относительно фиксированной точки равна работе A10, которую совершит электрическое поле при перемещении заряда q из точки в точку.Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки . Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.Работа, совершаемая электрическим полем при перемещении точечного зарядаq из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки .Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциаломφ электрического поля: . Потенциал φ является энергетической характеристикой электростатического поля.Работа A12 по перемещению электрического заряда q из начальной точки в конечную точку равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек: A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2). В Международной системе единиц (СИ) единицей потенциала является вольт (В).1 В = 1 Дж / 1 Кл.Во многих задачах электростатики при вычислении потенциалов за опорную точку удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно записать: ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ, где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует

49. Условия на границы двух диэлектриков для векторов E и D.

Обратимся теперь к нормальной составляющей вектора D. Воспользуемся для этого теоремой Гаусса для этого вектора. Выбирая поверхность интегрирования как показано на рис. 5.4 и следуя тем же рассуждениям, которые привели к выражению (5.18), получим D2n  D1n= Ђ.Из этого соотношения следует, что при наличии на границе раздела стороннего заряда с поверхностной плотностью Ђ нормальная составляющая вектора D терпит разрыв. При отсутствии стороннего заряда на границе.D1n = D2n.Нормальные составляющие вектора E с разных сторон границы раздела относятся тогда на основании , как. Как следует из полученных соотношений нормальная и тангенциальная составляющие вектора E на границе раздела ведут себя по разному. В результате линии вектора E испытывают преломление.Если среда 1 - проводник, а 2 - диэлектрик, то из соотношения (5.33) следует, что Dn = Ђ,где n - внешняя к проводнику нормаль.Если к заряженному проводнику прилегает однородный диэлектрик, то на границах диэлектрика выступают связанные поверхностные заряды.

47. Диэлектрики в электростатическом поле. Типы диэлектриков и механизм их поляризации. Связанные заряды. Вектор поляризованности и его связь с напряженностью. Связь поляризованности и плотности связанных зарядов.

В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.При внесении диэлектрика во внешнее электрическое поле E_0. в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов. Связанные заряды создают электрическое поле E, которое внутри диэлектрика направлено противоположно вектору напряженности E внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле E=E₀+E’ внутри диэлектрика оказывается по модулю меньше внешнего поля E. Физическая величина, равная отношению модуля напряженности E₀ внешнего электрического поля в вакууме к модулю напряженности E полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества. έ=E₀/E; Существует несколько механизмов поляризации диэлектриков. Основными из них являются ориентационная и электронная поляризации. Эти механизмы проявляются главным образом при поляризации газообразных и жидких диэлектриков.Ориентационная или дипольная поляризация возникает в случае полярных диэлектриков, состоящих из молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы представляют собой микроскопические электрические диполи – нейтральную совокупность двух зарядов, равных по модулю и противоположных по знаку, расположенных на некотором расстоянии друг от друга. Дипольным моментом обладает, например, молекула воды, а также молекулы ряда других диэлектриков (H2S, NO2 и т. д.).При отсутствии внешнего электрического поля оси молекулярных диполей ориентированы хаотично из-за теплового движения, так что на поверхности диэлектрика и в любом элементе объема электрический заряд в среднем равен нулю.При внесении диэлектрика во внешнее поле E₀ .При внесении диэлектрика во внешнее поле E0 возникает частичная ориентация молекулярных диполей. В результате на поверхности диэлектрика появляются нескомпенсированные макроскопические связанные заряды, создающие поле E’ направленное навстречу внешнему полю E0. У многих неполярных молекул при поляризации деформируются электронные оболочки, поэтому этот механизм получил название электронной поляризации. Этот механизм является универсальным, поскольку деформация электронных оболочек под действием внешнего поля происходит в атомах, молекулах и ионах любого диэлектрика.В случае твердых кристаллических диэлектриков наблюдается так называемая ионная поляризация, при которой ионы разных знаков, составляющие кристаллическую решетку, при наложении внешнего поля смещаются в противоположных направлениях, вследствие чего на гранях кристалла появляются связанные (нескомпенсированные) заряды. Примером такого механизма может служить поляризация кристалла NaCl, в котором ионы Na+ и Cl– составляют две подрешетки, вложенные друг в друга. В отсутствие внешнего поля каждая элементарная ячейка кристалла NaCl (см. Часть I § 3.6 ) электронейтральна и не обладает дипольным моментом. Во внешнем электрическом поле обе подрешетки смещаются в противоположных направлениях, т. е. кристалл поляризуется.При поляризации неоднородного диэлектрика связанные заряды могут возникать не только на поверхностях, но и в объеме диэлектрика. В этом случае электрическое поле связанных зарядов и полное поле могут иметь сложную структуру, зависящую от геометрии диэлектрика. Утверждение о том, что электрическое поле в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем строго справедливо только в случае однородного диэлектрика, заполняющего все пространство, в котором создано внешнее поле. В частности:Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд Q, то напряженность поля создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:

48. Теорема Гаусса для электростатического поля в диэлектриках. Вектор электрического смещения D

Поток вектора напряжённости сквозь сферическую поверхность радиуса R, охватывающую сферический заряд q, находившийся в её центре:(10)

Этот результат справедлив для замкнутой поверхности любой формы. Рассмотрим общий случай для произвольной поверхности, окружающей n зарядов.

В соответствии с принципом суперпозиции . Поэтому

,

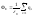
Эта формула выражает теорему Гаусса для электростатического поля:Поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённых на электрическую постоянную.Если заряд распределён с объёмной плотностью , то

или

Поле равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда .В качестве замкнутой поверхности возьмём цилиндр, ось которого перпендикулярна плоскости. Поток через боковые стенки цилиндра равен нулю, так как линии напряжённости перпендикулярны оси цилиндра и его образующей. Полный поток сквозь цилиндр равен сумме потоков через его основания.

Заряд внутри цилиндра согласно теореме Гаусса: 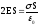, откуда.

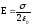1. Поле равномерно заряженной сферической поверхности.

Если r >R, то по теореме Гаусса получим:, где, откуда.

Если 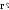<R, то замкнутая поверхность не содержит электрического заряда. Следовательно E = 0. Электри́ческая инду́кция или электрическое смещение — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации. D = ε0E + P.