11. Вращение тв. Тела вокруг неподвижной оси. Основное уравнение динамики вращательного движения твердого тела вокруг оси. Момент инерции. Теорема штейнера.

Вращ. вокруг неподвиж. оси наз. такое движение твердого тела, при котором во все время движ. две его точки остаются неподвиж. Прямая, проходящая через эти точки, наз. осью вращения. Все остальные точки тела движутся в плоскостях, перпенд. оси вращения, по окружностям, центры которых лежат на оси вращения.

Момент инерции системы относительно данной оси наз.физ.величина равная сумме произведений масс n мат.точек системы на квадраты их расстояний до рассматриваемой оси: J=mr². Кинетическая энергия вращающегося тела: T=Jω²/2.

Моментом силы Fотносительно неподвижно точки О называется физ.величина опр. Векторным произведением радиус-вектора r, проведенного из точки О в точку А, приложения силы, на силу F: M=[rF].

Осн у-е динамики вращ двж тверд тела. Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но dT=d(J_zω²/2)= J_zωdω, поэтому M_zdφ=J_zωdω, или M_zdφ/dt)= J_zω(dω/dt). Учитывая что ω= dφ/dt, получаем: M_z=J_z(dω/dt)= J_zε. J-главный момент инерции тела (момент инерции относительно главной оси).

Момент инерции системы(тела) относ данной оси наз физич вели, равн сумме произведений масс n матер точек сист на квадраты их расстояний до рассматриваемой оси.

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относ.любой другой парал.оси опред. Теоремой Штейнера: момент инерции тела J относ произв оси равен моменту его инерции Jс относ параллел оси, проходящ через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния между осями. J=Jc+ma².

18. Постулаты СТО. Относительность одновременности. Преобразования Лоренца

(СТО— теория, описывающая движение, законы механики и пространственно-временные отношения, определяющие их, при скоростях движения, близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей образует общую теорию относительности.

СТО полностью выводится на физическом уровне строгости из трёх постулатов (предположений):

1. Справедлив принцип относительности Эйнштейна — расширение принципа относительности Галилея.

2. Скорость света не зависит от скорости движения источника во всех инерциальных системах отсчёта.

3. Пространство и время однородны, пространство является изотропным.

Формулировка второго постулата может быть шире: «Скорость света постоянна во всех инерциальных системах отсчёта», но для вывода СТО достаточно его исходной формулировки Эйнштейном, записанной выше. Приписывание постулатов Эйнштейну правомерно в той степени, что до его работы эти уже сформулированные отдельно друг от друга (в частности, А. Пуанкаре) утверждения в совокупности явным образом никем не рассматривались.

Иногда в постулаты СТО также добавляют условие синхронизации часов по А. Эйнштейну, но принципиального значения оно не имеет: при других условиях синхронизации лишь усложняется математическое описание экспериментальной ситуации без изменения предсказываемых и измеряемых эффектов (см. по этому поводу работы в списке литературы).

Тем не менее, опора на достижения экспериментальной физики позволяет утверждать, что в пределах своей области применимости — при пренебрежении эффектами гравитационного взаимодействия тел — СТО является справедливой с очень высокой степенью точности (до 10−12 и выше). По меткому замечанию Л. Пэйджа, «в наш век электричества вращающийся якорь каждого генератора и каждого электромотора неустанно провозглашает справедливость теории относительности — нужно лишь уметь слушать».

Классические преобразования Галилеянесовместимы с постулатами СТО и, следовательно, должны быть заменены другими преобразованиями. Эти новые преобразования должны установить связь между координатами (x, y, z) и моментом времени t события, наблюдаемого в системе отсчета K, и координатами (x', y', z') и моментом времени t' этого же события, наблюдаемого в системе отсчета K'.

Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид: K' → K                K → K' 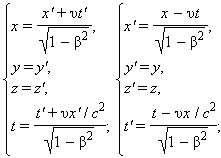β = υ /c.

14. Работа силы и ее выражение через криволинейный интеграл. Можность.

Энерг- универс мера различ форм движ и взаимодействия. С различ формами движ-я матер связ различ формы энерг: механич, теплов, элмагнтн, ядерн и др.в одних явл форма движ-я матер не изм (горяч тело нагрев холодн), в др-преход в иную форм( в результ трен механич движ превращ в теплов.) во всех случ энерг, отданная одним телом другому, равна энергии, получ последним телом.

Работой A, совершаемой постоянной силой Fназывается физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы Fи перемещения S.

Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

Элемент работой силы F на перемещ dr наз скаляр велич dA=Fdr=Fcos a ds=Fsds. где Fs-проекй вект F на dr. Работы силы на участке траектории от точки 1 до точки 2 равна алгеброич. сумме элементар. работ. на отдельно бесконечно малых участках пути: A= инт от1 до2 Fdscos a = инт от1до2 Fsds:

Мощн –скорость соверш раб. Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа: N=dA/dt. N=Fdr/dt . N=Fv. N-скалярн велич. В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

19. Следствия из преобразовании Лоренца. Лоренцово сокращение длины. Замедление хода движущихся часов.

Из преобразований Лоренца вытекает целый ряд следствий. В частности, из них следует релятивистский эффект замедления времени и лоренцево сокращение длины. Пусть, например, в некоторой точке x' системы K' происходит процесс длительностью τ0 = t'2 – t'1 (собственное время), где t'1 и t'2 – показания часов в K' в начале и конце процесса. Длительность τ этого процесса в системе K будет равна :

Аналогичным образом, можно показать, что из преобразований Лоренца вытекает релятивистское сокращение длины. Одним из важнейших следствий из преобразований Лоренца является вывод об относительности одновременности. Пусть, например, в двух разных точках системы отсчета K' (x'1 ≠ x'2) одновременно с точки зрения наблюдателя в K' (t'1 = t'2 = t') происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь :

Следовательно, в системе K эти события, оставаясь пространственно разобщенными, оказываются неодновременными. Более того, знак разности t2 – t1 определяется знаком выражения υ(x'2 – x'1), поэтому в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Этот вывод СТО не относится к событиям, связанным причинно-следственными связями, когда одно из событий является физическим следствием другого. Можно показать, что в СТО не нарушается принцип причинности, и порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.

Следствия из преобразований Лоренца : 1.одновремен событ в разн сист отсч. Если соб в сист К происх в одной точк и явл одновремен, то они явл одноврем и пространственно совп для люб инерц сист отсчета. Если соб в сист К простр разобщены,но одновремен, то в сист К1 эти событ,оставаясь простр разобщ,оказ и неодновремен. 2.длит соб в разн сист отсч.длит событ, происх в некот точк, наименьш в той инерц сист отсч, относ котор эта точк неподвиж. 3. длина в различ сист отсч. сокращ длины тем больш, чем больш скор движ, а попереч разм не завис. Релят зак слож скор:(см с обр стор).скор света в вак-предельн скор, котор нельзя превыс.преоб Лор. привод к выв о относ длин и промеж вр, в то же вр относит характер длин и вр в теор Эйншт,озн относ-ть отдельн комп какой-то физ велич,не зав от сист отсч, т.е инвариантн.В 4-х мерн простр эта велич – интерв межд 2-мя событ.

Лоренцевское сокращение длины. Рассмотрев движение светового импульса вдоль оси x, и потребовав (на основании постулата одинаковости скорости света во всех инерциальных системах отсчёта), чтобы расстояние между двумя точками было всегда равно времени, за которое свет идёт от одной точки до другой, делённому на (константу) скорость света, можно получить фактор сокращения расстояний вдоль оси x, а учитывая, что смещение начала отсчёта − Vt очевидно, можно получить и преобразование для x: X’=x-Vt/sqrt(1-V²/c²)

Замедление времени. Показать, что любые процессы (например ход часов) выглядит медленнее из системы отсчета где носитель этого процесса (например часы) движется, чем в его собственной системе отсчета (в которой он неподвижен), и найти количественно фактор такого замедления, можно, рассмотрев мысленный эксперимент со «световыми часами», представляющими собой источник и приемник света, удаленные друг от друга на известное фиксированное расстояние L, и отмеряющие, таким образом, интервал времени L/c, соответствующий времени прохождения света от источника до приемника (это можно непрерывно повторять). Все другие часы, из принципу относительности, должны идти точно так же.

Для более прямого соответствия формы полученного результата формуле прямого преобразования Лоренца, будем считать, что наши световые часы покоятся в нештрихованой системе отсчета K, штрихованая же система отсчета K' пусть движется для определенности вправо вдоль оси x со скоростью V. Источник и приемник расположим вдоль оси y при x=0. Это частный случай, который позволит нам получить сперва отдельно частное и более простое преобразование для времени.

L’=l0*sqrt(1-(U/c)2)/ Время, согласно преобразованиям Лоренца относительно, и зависит от системы отсчета. Представим себе два одинаковых космических корабля движущихся с высокими скоростями в противоположные скорости. Космонавт первого космических корабля будет видеть, что второй корабль короче чем у него. Космонавт же второго корабля будет видеть первый корабль короче. Аналогично со временем. Оба космонавта чистят зубы за 5 минут. Но в подобной ситуации первый космонавт будет чистить зубы дольше чем 5 минут по часам второго. Второй же будет чистить дольше чем первый. Здесь совершенно невозможно сказать одновременно они закончили чистить зубы или нет. Простое Ньютоновское понятие одновременности здесь не работает! Как видно из формул преобразования Лоренца смешивают понятие пространства и времени. Именно поэтому в космологии употребляют понятие четырехмерное пространство-время. В нем нет понятия одновременности.

20. Пространственно временно интервал между событиями и его инвариантность. Инварианты преобразований Лоренца

Интервал в теории относительности — расстояние между двумя событиями в пространстве-времени, являющееся довольно прямым обобщением евклидовского расстояния между двумя точками — на пространство-время (определение см. ниже). Интервал лоренц-инвариантен, то есть не меняется при переходе от одной инерциальной системы отсчёта к другой, или, говоря иначе, является инвариантом (скаляром) в специальной и общей теории относительности.

Это свойство интервала делает его фундаментальным понятием, на основе которого может, в соответствии с принципом относительности, быть осуществлена ковариантная формулировка физики (то есть формулировка, законы которой записываются одинаково в любой инерциальной системе отсчета), и роль интервала при этом почти столь же велика, как роль обычного расстояния в обычной (евклидовской или римановой) геометрии.

В частности, преобразования Лоренца (преобразования координат, включая время, оставляющие неизменной запись всех фундаментальных уравнений физики при замене системы отсчета) могут быть формально найдены как группа преобразований, сохраняющих инвариантным интервал.

Напрямую из принципа относительности, однородности и изотропности пространства, а также однородности времени следует, что при переходе от одной ИСО (инерциальной системы отсчёта) к другой ИСО интервал остается неизменным. Именно это его свойство позволяет формально вывести преобразования Лоренца и обосновывает оправданность введения пространства Минковского и неримановой метрики.

Инвариантность скорости света здесь имеет значение потому, что известно, что скорость света всегда одинакова хотя бы в одной системе отсчёта, а из этого и из принципа относительности следует, что она должна быть такой же в любой ИСО. Однако вместо скорости света можно было бы взять максимальную скорость движения тел или распространения взаимодействий, которая также, из принципа относительности, должна быть одинакова во всех инерциальных системах отсчёта. Если максимальная скорость распространения взаимодействий конечна, она, вследствие принципа относительности, должна совпадать со скоростью света, которую будем здесь обозначать, как обычно, C.

Для приводимого ниже доказательства существенно, что мы будем считать все изменения пространственных координат и времени малыми (бесконечно малыми), то есть всё будет формулировано для интервала между двумя бесконечно близкими в пространстве и времени событиями.

Пространственно-временной интервал определяется в СТО следующим соотношением: S12=sqrt(c²t²12-l²12)

С помощью преобразований Лоренца можно доказать, что пространственно-временной интервал между двумя событиями не изменяется при переходе из одной инерциальной системы в другую. Инвариантность интервала означает, что, несмотря на относительность расстояний и промежутков времени, протекание физических процессов носит объективный характер и не зависит от системы отсчета. Если одно из событий представляет собой вспышку света в начале координат системы отсчета при t = 0, а второе – приход светового фронта в точку с координатами x, y, z в момент времени t, то: x2 + y2 + z2 = c2t2, и, следовательно, интервал для этой пары событий s = 0. В другой системе отсчета координаты и время второго события будут другими, но и в этой системе пространственно-временной интервал s' окажется равным нулю, так как : x’²+y’²+z’²=c²t’². Для любых двух событий, связанных между собой световым сигналом, интервал равен нулю.

12. Инерциальные системы отсчета. Механический принцип относительности и преобразования Галилея. Закон сложения скоростей в Ньютоновской механиеке.

Инерциальная система отсчёта, система отсчёта, в которой справедлив закон инерции: материальная точка, когда на неё не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения. Всякая система отсчёта, движущаяся по отношению к И. с. о. поступательно, равномерно и прямолинейно, есть также И. с. о. Следовательно, теоретически может существовать сколько угодно равноправных И. с. о., обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (так называемый принцип относительности). Помимо закона инерции, в любой И. с. о. справедливы также 2-й закон Ньютона и законы сохранения количества движения (импульса), момента количества движения и движения центра инерции (или центра масс) для замкнутых, т. е. не подверженных внешним воздействиям, систем.

Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета - иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-то конкретной из инерциальных систем отсчета. Также - поэтому - не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея.

В класич механ справедл механ принцип относ(принц отнтосит Галилея): законы динамики оинак во всех инерц сист отсчета.Рассм сист К(условн неподвиж) и К1(движ отнс К).найдем связь межд коорд произ точк А в обеих сист. r =r1+r0=r1+Ut. это у-е можн зап в проекц на оси коорд: x= x1+Uxt (так же для y и z, U-скорость). Все эти у-я наз преобр коорд Галилея.

Продиференц выраж r =r1+r0=r1+Ut по времени( с учетом, что t=t1) получим у-е: V=V1+U1, котор представл собой правило слож скоростей в класич мех.

При рассмотрении сложного движения (то есть когда точка или тело движутся в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта. В классической механикеабсолютная скоростьточки равнавекторнойсумме еёотносительнойипереноснойскоростей:

Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.