1.Кинематическое описание движения материальной точки. Перемещение. Путь. Уравнение движения. Скорость и ускорение как производные радиус-вектора по времени.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь.

При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями

x = x(t), у = y(t), z = z(t),

эквивалентными векторному уравнению

r = r(t).

Число независимых координат, полностью определяющих положение точки в про­странстве, называется числом степеней свободы.

Траектория движения материальной точки — линия, описыва­емая этой точкой в пространстве.

Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути s и является скалярной функцией времени: s = s(t). Вектор r = r — r₀, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.

Перемещение - векторная величина, равная радиусу-вектору, проведенному от начальной точки траектории к ее конечной точке.

Путь - длина участка траектории материальной точки, пройденного ею за определенное время.

Уравнение движения (уравнения движения) — уравнение или система уравнений, задающие закон эволюции механической или сходной динамической системы

Рассмотрим в рамках ньютоновской механики точечную частицу, способную перемещаться лишь по одной прямой (например, бусину, способную скользить по гладкой спице). Будем описывать положение частицы на прямой единственным числом - координатой - x. Пусть на эту частицу действует (например, со стороны некоторой пружины) сила f, зависящая от положения частицы по закону Гука, то есть, выбрав удобное начало отсчета x, можем записать f = - k x. В таком случае, учитывая второй закон Ньютона и кинематические соотношения, обозначив скорость как v, будем иметь следующие уравнения движения для нашей системы:

или, исключая v из системы:

Подставив начальную координату и скорость в правые части этих уравнений, и заменив бесконечно малое dt на малое, но конечное, δt, и переписав приближенно в соответствии с этим уравнения в первой форме - в виде величина(t + δt) = величина(t) + производная·δt, получим:

,

и переходя от предыдущего момента к следующему (каждый раз время растет на δt), можем получить численное решение этих уравнений движения в виде таблицы 

, приближенно представляющей зависимость x(t) и v(t) от времени (с шагом δt). Можно увидеть, что, если δt было выбрано достаточно малым, что x(t) и v(t) очень близко совпадают с функцией .

Использовав для догадки это приближенное решение или какие-то другие соображения, можем, если мы уже подозреваем, каким должно быть решение, просто подставить

,

где A,ω,φ - просто постоянные, в точные уравнения движения, взяв нужные производные по времени от этого выражения. При этом мы смоожем убедиться, что нетрудно подобрать конкретные значения A,ω,φ, чтобы равенство при этой подстановке выполнялось, а также найти необходимые для этого значения A,ω,φ (оказывается, A и φ могут быть любыми, а . Мы получили таким образом точное решение уравнений движения, да еще и общее точное решение (то есть подходящее для любых начальных условий, в чём нетрудно убедиться).

Теперь, имея это общее точное решение, мы можем выбрать из множества общих решений (с разными A и φ) частное решение, удовлетворяющее конкретным начальным условиям. Так мы решим задачу для заданного уравнения движения и начальных условий.

Скорость и ускорение как производные радиус-вектора по времени.

Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r₀ (рис. 3). В течение малого промежутка времени t точка пройдет путь s и получит элементарное (бесконечно малое) перемещение r.

Вектором средней скорости <v> называется отношение приращения r радиу­са-вектора точки к промежутку времени t:

Направление вектора средней скорости совпадает с направлением r. При неог­раниченном уменьшении t средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пре­деле совпадает с касательной, то вектор скорости v направлен по касательной к траек­тории в сторону движения (рис. 3). По мере уменьшения t путь s все больше будет приближаться к |r|, поэтому модуль мгновенной скорости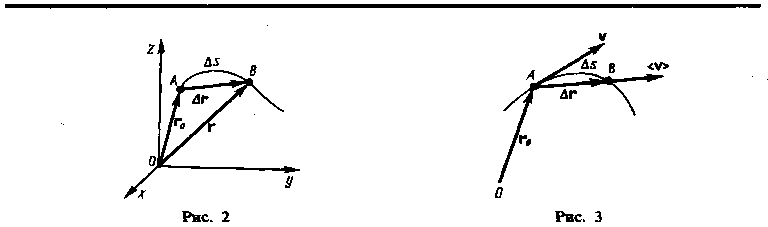

Таким образом, модуль мгновенной скорости равен первой производной пути по времени:

При неравномерном движении — модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной v — средней скоро­стью неравномерного движения:

Из рис. 3 вытекает, что v> |v|, так как s > |r|, и только в случае прямолиней­ного движения

Если выражение ds = vdt (см. формулу (2.2)) проинтегрировать по времени в пре­делах от t до t + t, то найдем длину пути, пройденного точкой за время t:

В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид

Д лина пути, пройденного точкой за промежуток времени от t₁ до t₂, дается интегралом

2. Кинематика вращательного движения твердого тела. Угловая скорость. Угловое ускорение. Связь линейных и угловых характеристик движения.

Модуль вектора равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта (рис.6). Векторы, направления которых связываются с направлением вращения, назы­ваются псевдовекторами или аксиальными векторами. Эти векторы не имеют опреде­ленных точек приложения: они могут откладываться из любой точки оси вращения.Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Вектор направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор (рис.7). Размерность угловой скоростиdim =T^–1, а ее единица — ради­ан в секунду (рад/с).

Линейная скорость точки (см. рис. 6)

т. е.

В векторном виде формулу для линейной скорости можно написать как векторное произведение:

При этом модуль векторного произведения, по определению, равен , а направление совпадает с направлением поступательного движения правого винта при его вращении от кR.

Если (=const, то вращение равномерное и его можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2. Так как промежутку времени t = T соответствует = 2, то = 2/T, откуда

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

откуда

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору, при замедлен­ном — противонаправлен ему

Тангенциальная составляющая ускорения

Нормальная составляющая ускорения

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение , нормальное ускорение) и угловыми величинами (угол поворота, угловая скорость , угловое ускорение ) выражается следующими формулами:

В случае равнопеременного движения точки по окружности (=const)

где ₀ — начальная угловая скорость.

3. Криволинейное движение материальной точки. Скорость и ускорение при криволинейном движении. Тангенциальное и нормально ускорение.

Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости движения в любой точке траектории направлен по касательной к ней. Допустим, что в точке М0 траектории скорость было , а в точке М стала. При этом считаем, что промежуток временипри переходе точки на путииз М0 в М настолько мал, что изменением ускорения по величине и направлению можно пренебречь. Для того, что бы найти вектор изменения скорости, необходимо определить векторную разность:.Используя уравнение:. При бесконечном уменьшенииуголпри вершинестремится к нулю. Тогда векторомможно пренебречь по сравнению с вектором, а векторбудет выражать тангенциальное ускорение и характеризовать быстроту изменения скорости движения по численному значению. Следовательно, тангенциальной ускорение численно равна производной от скорости по времени:и направленно по касательной к траектории. Вычислим векторназываемый нормальным ускорением. При достаточно маломучасток криволинейной траектории можно считать частью окружности. В этом случае радиусы кривизны М0О и МО будут равны между собой и равны радиусу окружности R. Поэтому, но, тогда. Переходя к переделу прии учитывая, что при этом, находим,т.е.. Так как приугол, направление этого ускорения совпадает с направлением радиуса R кривизны или с направлением нормали к скорости , т.е. ускоренияперпендикулярен. Поэтому это ускорение называют центростремитель-ным. Оно характеризует быстроту изменения скорости движения по направлению. Полное ускорение определяется векторное суммой тангенциального и нормального ускорений:.

Направление полного ускорения определяется углом между a₁ и a_n :

4. Динамика материальной точки. Механическое движение как простейшая форма движения материи. Пространство и время. Модели в механике: материальная точка и абсолютно твердое тело. Основные задачи механики.

Основная задача динамики - изучение законов движения тел и причин, кото- рые вызывают или изменяют это движ.

Масса-опред инерцион и гравитац св-ва

Импульс- велич, равн произв массы на скорость и имеющ направл скрости. P=mv – количество движения.

Сила- вект велич, явл мерой механич воздействия на тело со стороны др тел или полей, в результате которого тело приобретает ускорение или измен свою форму и размеры. 1зак:если F=0,то v=0 или v=const.

2зак:F=ma

3зак:F= -F.

У-е движ-я матер точки: F= ma=m*dv/dt.но m-пост велич =>F=d* *(mv)/dt=>F=dp/dt.

Границы применения. законыНьютона позв осущ переход от динам матер точк к динамике систем мат точек. Это след из того, что и для сист мат точ взаимод свод к силам парного взаимодействия межд мат точками.

Любое движение тв.тела можно представить как комбинацию поступательного и вращ. движения.

Движ.тел происходит в пространстве и во времени. Поэтому для описан.мат.точки надо знать в каких местах пространства эта точка находилась и в какие моменты времени она проходило то или иное положение. Положение мат.точки опр. по отношению к какому либо другому, произвольно выбранному телу, наз.телом отсчета. С ним связывается система отсчета – совокупность системы координат и часов, связанных с телом отсчета.

Простейшей моделью является мат. точка- тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Пример: движение планет по орбитам вокруг солнца. Произв. макроскопическое тело можно мысленно разбить на малые взаимодействующие части, каждая из которых будет рассматриваться как мат.точка. Тогда изучение сводится к изучению системы мат.точек.

Абсолютным твердым телом называется тело, которое ни при каких условиях не может диформироваться и при все условиях расстояние между двумя точками этого тела остается постоянным.

Прямая задача динамики: по заданным силам определить характер движения тела.

Обратная задача динамики: по заданному характеру движения определить действующие на тело силы.

8. Консервативные и неконсервативные силы. Потенциальная энергия частицы во внешнем силовом поле и связь ее с консервативной силой. Потенциальная энергия системы частиц.

Потенциальная энергия — механическая энергия системы тел, определяемая их вза­имным расположением и характером сил взаимодействия между ними.

Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, — консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипатнвной; ее примером является сила трения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении кон­фигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:РаботаdA выражается как скалярное произведение силы F на перемещение dr и выражение можно записать в виде

Следовательно, если известна функция П(r), то из формулы можно найти силу F по модулю и направлению.

Потенциальная энергия может быть определена исходя из) как

где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точ­ностью до некоторой произвольной постоянной. Это, однако, не отражается на физи­ческих законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энер­гию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают от­носительно нулевого уровня. Для консервативных сил

или в векторном виде

где

(i, j, k — единичные векторы координатных осей). Вектор, определяемый выражением, называется градиентом скаляра П.

Для него наряду с обозначением grad П применяется также обозначение П.  («набла») означает символический вектор, называемый оператором Гамильтона* или набла-оператором:

7. Механическая система. Внешние и внутренние силы. Третий Закон Ньютона. Замкнутая система тел. Закон сохранения импульса.

Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокуп­ность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механичес­кой системы называются — внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и проти­воположно направлены, т. е. геометрическая сумма внутренних сил равна нулю. Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны m₁, m₂,.... m_n, и v₁, v₂,..., v_n. Пусть — равнодейст­вующие внутренних сил, действующих на каждое из этих тел,a — равно­действующие внешних сил. Запишем второй закон Ньютона для каждого изn тел механической системы:

Складывая почленно эти уравнения, получаем

Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то

илигде— импульс системы. Таким образом, производная по времени от им­пульса механической системы равна геометрической сумме внешних сил, действующих на систему.В случае отсутствия внешних сил (рассматриваем замкнутую систему)

Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выпол­няется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импуль­са — фундаментальный закон природы.