АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра ЭЛЕКТРОНИКИ

Бахтаев Ш.А.

Задания для РГР по дисциплине

Метрология, стандартизация и сертификация

для студентов факультета РТС

Алматы 2012

1 ИЗМЕРЕНИЕ ТОКА

Задача 1.1

Ток в цепи, запитаемый от источника высокой частоты G1 измеряется прибором магнитоэлектрической системы ИМ с термопреобразователем ТП (рисунок 1).

Определите:

а) ток в цепи;

б) погрешность измерения тока;

в) дополнительную погрешность за счёт токов утечки;

г) общую погрешность измерения;

д) укажите правильное место включения прибора.

Руководство к выполнению

Рисунок 1.1 – Схема измерения ВЧ – тока

Измеряемый прибором ток равен

Iх =, (1.1)

где Iс – ток утечки через параллельно включенные ёмкости;

С₁₃ = С₂₃ = 2,5 пФ;

I_н – ток нагрузки.

Токи, протекаемые в цепях схемы, обратно пропорциональны их сопротивлениям

X_c /Z_н = (1/ (ωC_э))/Z_н = К_с, (1.2)

где С_э = С₁₃ = С₂₃ = С.

Поэтому

I_x = = I_н (1.3)

Дополнительная погрешность за счёт токов утечки

δ_y = (-1) · 100, % (1.4)

Основная погрешность возникает за счёт РА

δа = (± ∆а /I_х) 100, (1.5)

где ∆а = ± γа · Iан /100, (1.6)

γа = 2,5 % - класс точности РА;

Iан = 5мА. - предел измерения.

Общая погрешность измерения

δ = | δа | + δу, %. (1.7)

Таблица 1.1

Нагрузка	Вариант, предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
Zн, кОм	20	25	30	22	27	35	32	37	18	33
φн, град	15	17	20	22	25	27	31	35	38	42

Таблица 1.2

Частота	Вариант, последняя цифра зачётной книжки
	0	1	2	3	4	5	6	7	8	9
f, МГц	1	2	4	6	8	10	0,8	0,9	0,7	7

Задача 1.2

Измерить ток в антенне передатчика при помощи трансформатора тока высокой частоты и амперметра с термопреобразователем РА.

Найдите:

a) ток в антенне;

б) погрешности измерения тока в антенне, если все средства измерения выполнены по классу точности 2,5;

Руководство к выполнению

Рисунок 1.2 – схема измерения

Ток в антенне определяется как

Iа = In К_Т , (1.8)

где In – ток, показываемый прибором;

К_Т = w₂ / w₁ – коэффициент трансформации трансформатора тока.

С учётом погрешностей выражение (1.8) имеет вид

(Iа ± ∆а) = (In ± ∆п) · (К_Т ± ∆К_Т), (1.9)

где ∆а – абсолютная погрешность тока в антенне;

∆п = ± γп Iпн / 100 (Iпн = 10мА); (1.10)

γп – класс точности РА;

∆К_Т = ± γт К_Т / 100; (1.11)

γт – класс точности ТТ.

Относительная погрешность измерения равна

δа = ± ∆а / Iа. (1.12)

Таблица 1.3

Число витков	Предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
ω2, витки	50	75	100	125	150	60	70	80	100	130

Таблица 1.4

Ток прибора	Последняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
In, мА	2	4	6	8	10	3	5	7	9	1

Задача 1.3

Ток в электрической цепи на ВЧ определён путём измерения поглощаемой мощности Р на сопротивлении нагрузки R_н , имеющей класс точности 0,5. Мощность измерялась калориметрическим ваттметром класса точности 1,5 со шкалой 0…10 Вт.

Определить:

а) Ток в цепи;

б) Абсолютный предел изменения погрешностей;

в) Результат измерения.

Руководство к выполнению

Данное измерение является косвенным измерением

I = (1.13)

Пределы абсолютной погрешности тока можно найти

∆_I = ± , (1.14)

где ∆_Р – абсолютная погрешность ваттметра,

∆R_н – абсолютная погрешность изготовления сопротивления нагрузки.

Тогда

I_x = I ± ∆_I (1.15)

Таблица 1.5

Мощность	Последняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
Р, Вт	5	10	15	20	25	30	35	40	45	50

Таблица 1.6

Нагрузка	Последняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
Rн, Ом	50	75	125	150	200	250	300	350	400	450

2 ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ

Задача 2.1

Электрическое напряжение звуковой частоты измеряется электронным вольтметром на один предел измерения 10 В класса точности 2,5 с различными детекторами на входе:

а) средневыпрямленного значения (СВЗ);

б) амплитудного значения (АЗ) с открытым входом (АЗО)

и с закрытым входом (АЗЗ);

в) среднеквадратического значения (СКЗ). На вход этих вольтметров одновременно подаётся напряжение определённой формы (таблица 2.1).

Определите:

а) Показания каждого вольтметра;

б) Погрешность измерения напряжения.

Руководство для выполнения

Рисунок 2.1 – схема измерения

Шкала всех вольтметров проградуирована в действующих значениях синусоидального пятидесяти переходного напряжения.

Вольтметр с детектором СВЗ реагирует на среднее значение за период. Вольтметр с АЗО – детектором реагирует на максимальные значения измеряемого напряжения. Вольтметр с АЗЗ – детектором реагирует на амплитудные значения переменной части измеряемого напряжения.

Вольтметр с СКЗ – детектором реагирует на действующее значение напряжения. Коэффициенты формы и амплитуды различных форм кривых напряжений приводятся в учебниках по ТОЭ.

Общая погрешность измерения напряжения будет определяться по формуле

δ = |δв| + |δ_д| (2.1)

где δв = (± ∆в/Uэ)100;

∆в = ± γвUн /100;

Uэ – показания вольтметра в случае эквивалентного синусоидального напряжения с параметрами Um, Т;

δд =,

где U – показания прибора при заданной форме напряжения.

Таблица 2.1

Вариант, последняя цифра шифра	Сигнал	Вариант, последняя цифра шифра	Сигнал
0		5
1		6
2		7
3		8
4		9

Таблица 2.2

Параметры сигнала	Вариант, предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
А = Um, B	3	3,5	4	4,5	5	5,5	6	6,5	7	8
f, кГц	0,5	0,6	0,7	0,8	0,9	1,0	1,5	1,6	1,8	2

Задача 2.2

В начале и конце линии связи, соединяющих станции А и В, измерены напряжения Uа и Uб. Измерения выполнены однотипными вольтметрами, шкала которых проградуирована в децибелах (дБ). Фактически измерительный механизм вольтметров рассчитан на пределы 0…5 В и имеет класс точности 1,0.

Определите:

а) абсолютные уровни напряжения в точках А и В;

б) относительный уровень напряжения в точке В;

в) абсолютную и относительную погрешность измерения уровня в точках А и В;

Постройте:

а) шкалу вольтметра в вольтах;

б) шкалу вольтметра в децибелах.

Руководство к выполнению

Шкала вольтметра в децибелах градуируется в соответствии с выражением

p_ua = 20lg · (U/ 0,775), [дБ]. (2.2)

где U – напряжение, в В.

Абсолютные уровни рассчитываются в соответствии с формулой (2.2), предварительно найдя значение U по данным p_ua, p_uв.

Относительные уровни можно определить по формуле

p_uo = 20lg · (U_b/ U_a), [дБ]. (2.3)

Абсолютные погрешности можно найти по известной формуле приведённой погрешности. Относительная погрешность измерения находится по формуле

δ_u = ± γ_u · (U_н/ U), (2.4)

где U_н = 5В, U – измеренное значение напряжения в вольтах.

Для того чтобы определить напряжение сигнала в вольтах по показанию вольтметра со шкалой в децибелах, необходимо найти.

U = 0,775 · 10^{0,05 p}ua (2.5)

Рисунок 2.2 – Точки измерения

Таблица 2.3

Уровень напряжения	Вариант, предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
pua, дБ	16	15,7	14,8	15,2	15,5	14,9	14,8	14,3	14	13,8

Таблица 2.4

Уровень напряжения	Вариант, последняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
puв, дБ	11,7	11,5	11,2	11	10,8	10,6	10,4	10,0	9,5	9,2

Задача 2.3

Измеренное напряжение содержит в своём составе, кроме основной частоты высшие гармонические составляющие (К = 3,5,7,9). Данное напряжение определяется абсолютными уровнями напряжения в децибелах (таблица 2.5).

Определите:

а) действующее напряжение сети U_с;

б) действующее напряжение высших гармонических составляющих U_r;

в) коэффициент нелинейных искажений.

Постройте:

осциллограмму напряжения сети.

Руководство к выполнению

Абсолютные уровни напряжения определяются по формуле (2.2). Перевод этих уравнений в напряжение в вольтах производится по формуле (2.5).

Показания электродинамического вольтметра (частотный диапазон 50 – 450 Гц) зависят от действующего значения измеряемого напряжения

U_c = (2.6)

Действующее значение напряжения (2.6) гармоник можно измерить электронным вольтметром с детектором СКЗ и режекторным фильтром на входе

U_г = (2.7)

Коэффициент нелинейных искажений есть отношение

К_ни = (U_г/U_c) · 100, %. (2.8)

Для построения кривой (осциллограммы) напряжения на одном периоде следует задать аналитическое выражение для мгновенного значения напряжения

U_c = , (2.9)

где U_mk – амплитуда гармоники;

φ_k – фаза к-ой гармоники относительно первой;

ω = 2πf (f = 50 Гц).

Таблица 2.5

Вариант, предпоследняя цифра шифра	Уровень гармоники; puk дБ и их фазовый угол сдвига; φk, град
	1		3		5		7		9
	U	φ, ˚	U	φ, ˚	U	φ, ˚	U	φ, ˚	U	φ, ˚
0	48,4	-2	18,6	-10	19,9	-12	17	-8	12,6	-5
1	48,6	-3	18,9	-20	19,6	-18	17,1	-12	12,3	-17
2	49,3	2	17,7	-30	19,4	-25	17,2	-18	12	-25
3	48,7	2,5	18	10	19,1	12	17,3	8	12,8	-33
4	48,8	0	18,5	20	20,0	18	16,9	12	13	5
5	49,1	0	17,8	30	20,2	25	16,7	18	13,2	17
6	49,2	-1,5	19,0	45	20,3	-7	16,5	-10	12,4	25
7	49,3	1,5	19,1	60	20,4	-12	17,5	-15	11,8	33
8	48,9	1,6	19,2	-45	19,8	-22	17,7	-24	11,7	-12
9	49,4	1,8	19,3	-60	19,7	-27	17,8	-27	10,5	-15

3 ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

3.1 Измерение сопротивления методом амперметра – вольтметра

Задача 3.1

Для измерения неизвестного сопротивления использованы приборы: амперметр класса точности γ_а = 1,5 на предел измерения I_ан = 2,5 А со шкалой α_ан=75 дел.; вольтметр класса точности γ_в=1,0 на пределе измерения U_вн = 15 В со шкалой α_вн = 75 делений. Амперметр показал α_а делений, его вольтметр α_в делений (таблица 3.1; 3.2).

Определите:

а) Неизвестное сопротивление R_x;

б) Пределы абсолютной ∆ и относительной δ погрешности;

в) Результат измерения.

Нарисуйте: правильную схему измерения.

Руководство к выполнению

Неизвестное сопротивление есть результат косвенного измерения

R = U_в/I_a, (3.1)

где U_в, I_a – показания вольтметра (в В) и амперметра (в А).

Пределы абсолютной погрешности измерения определяются как

∆(R_x) = ± , (3.2)

где ∆U_в, ∆I_a – абсолютные погрешности вольтметра и амперметра (аналогично формуле (1.10)).

Относительная погрешность сопротивления определяется как

δ(R) = ± (∆(R)/R) ·100, %. (3.3)

Надо определить методическую погрешность δ_n(R). Она определяется схемой включения приборов: схема для измерения малых и схема для измерения больших сопротивлений. Первая применяется в том случае, если

R_x < = R_э, (3.4)

где R_a = 0,015 Ом, R_в – внутреннее сопротивление амперметра и вольтметра (для вольтметра задаётся обычно ток полного отклонения I_в = 3мА).

Если R_x, больше R_э, то применяется вторая схема. Методическая погрешность для этих схем приведена в (4).

Общая относительная погрешность измерения

δ = |δ(R)| + |δ_м(R)|. (3.5)

Так как δ = (∆/R) ·100, то

∆ = (δ∙R)/100.

Результат измерения

R_x = (R ± ∆) Ом.

Таблица 3.1

Показания амперметра	Вариант последняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
γа, дел	35	37	40	45	50	55	60	65	70	58

Таблица 3.2

Показания вольтметра	Вариант предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
αв, дел	73	70	67	65	62	60	58	55	52	50

Рисунок 2.2 – Схема измерения сопротивлений методом вольтметр-амперметра

При включении перемычки П3 и выключении перемычек П1 и П2 из схемы измерений, показанной на рисунке 1, а, можно исключить измерительные приборы, а поочерёдным включением перемычек П1 и П2 включить вольтметр до и после миллиамперметра.

3.2 Измерение ёмкостного сопротивления

Измерение сопротивления ёмкости производится по схеме одного амперметра при стабильном источнике питания U_n = 100 В с частотой f = 400Гц и со стабильностью 0,5 %. Погрешность установки частоты

∆f = ± (0,01f + 2) Гц. (3.6)

При проведении измерений использовался миллиамперметр класса точности γ_а = 1,0 на предел измерения I_ан = 30 мА. Прибор показал ток I (таблица 3.3).

Найдите:

а) Значение ёмкости;

б) Общую погрешность измерения.

Нарисуйте cхему измерения.

Руководство к выполнению

Ёмкостное сопротивление равно

X_c = 1/ ω C = U/I. (3.7)

Из выражения (3.7) получим

С = I/2πfU = 0,159 · (I/fU). (3.8)

Обозначим Х₁ = I, X₂ = U, X₃ = f, тогда пределы погрешностей найдём

∆_с = ± , (3.9)

где ∆_xi , ∆– абсолютные погрешности параметров источника питания и миллиамперметра.

С_Х = С ± ∆_С (3.10)

Таблица 3.3

Показание амперметра	Вариант, предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
I, мА	5	7,5	10	12,5	15	17,5	20	22,5	24	23

3.3 Измерение индуктивного сопротивления

Задача 3.3

Измерение индуктивного сопротивления производится по схеме амперметра и вольтметра. Амперметр на номинальный ток I_Н = 30мА имеет внутреннее сопротивление R_A = 0,1 Ом, шкалу на α_АН = 100 делений, класс точности γ_А = 1,0. Вольтметр на ток полного отклонения I_ВН = 3 мА и на номинальное напряжение U_ВН = 25 В имеет класс точности γ_В = 0,5 и шкалу на α_ВН = 100 делений. Приборы показали значения тока I (таблица 3.4) и напряжение U (таблица 3.5).

Найдите:

а) Измеряемую индуктивность при допущении, что активное

сопротивление катушки индуктивности мало;

б) Погрешность измерения индуктивности за счёт инструментальной и методической погрешности.

Нарисуйте: Схему измерения индуктивности.

Руководство к выполнению

Измерение индуктивности производится на рабочей частоте 1 кГц. Индуктивное сопротивление равно

Х_L = ωL = U/I (3.11)

Из (3.11) имеем

L = (1/2πf) · (U/I) (3.12)

Дальнейшие расчёты выполняются по методу и подобию предыдущих задач этого раздела

Таблица 3.4

Показание амперметра	Вариант, предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
I, мА	10	12	14	16	18	20	22	24	15	17

Таблица 3.5

Показания вольтметра	Вариант, последняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
U, В	24	22	20	18	16	14	15	17	19	21

4 МОСТОВОЙ МЕТОД ИЗМЕРЕНИЯ

4.1 Определение места повреждения линии связи

Задача 4.1

На рисунке 4.1 представлена двухпроводная линия связи

Рисунок 4.1 – Двухпроводная линия связи

В точке С произошло повреждение изоляции (или разрыв) провода. Пользуясь специализированным мостом (рисунок 4.2) определить место повреждения линии связи, если известно, что жилы провода выполнены медным проводом марки МО и сечением S.

Рисунок 4.2 – Схема моста Муррея при эксплуатационных измерениях

Руководство к выполнению

Уравнение равновесия моста наблюдается при выполнении условия

r_x = R₁/(R₁+R₂) · (r_x + r_y + r_o) = R₁/(R₁+R₂) · 2r_o, (4.1)

где r_o – сопротивление исправной жилы.

Зная марку провода (кабеля), а значит сечение жилы и удельное сопротивление жилы ρ, найдём длину линии связи от начала 1н до точки пробоя С

l_x = r_x · (S/ρ), (4.2)

где r_x из выражения (4.1), в Ом;

S - сечение, мм² (принять 1,5 мм²);

ρ – удельное сопротивление, Ом/м² (0,01673).

Таблица 4.1

Параметры	Вариант, последняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
l, км	10	12	14	20	15	18	17	23	25	20
R1, Ом	60	70	80	100	90	85	75	90	70	80
R2, Ом	990	950	980	990	970	995	1000	985	965	970

4.2 Измерение ёмкости

Задача 4.2

Четырёхплечий мост уравновешен при определённых значениях параметров его плеч.

Определите:

а) Ёмкость С₁, если известны параметры мостовой цепи при равновесии

(таблица 4.2).

б) Тангенс угла диэлектрических потерь

Руководство к выполнению

Мостовая схема для измерения ёмкости позволяет сравнить измеряемую ёмкость С₁ с ёмкостью образцового конденсатора С₀, включенного в соседнее плечо.

Рисунок 4.2 – Схема моста для измерения параметров конденсатора

При равновесии моста (судим по отсутствию тока в нуль - индикаторе) получим равенство

(r_x + 1/jωc₁) · R₂ = (r₀ + 1/jωc₀) · R₁ (4.3)

Из уравнения равновесия (4.3) нетрудно получить выражение

С₁ = С₀R₂/R₁; (4.4)

r₁ = r₀R₁/R₂; (4.5)

tgδ₁ = r₁/x_С1 = ωr₁С₁ = ωr₀С₀. (4.6)

Таблица 4.2

Параметры мостовой цепи	Вариант, предпоследняя цифра шифра
	0	1	2	3	4	5	6	7	8	9
R2, Ом	2000	1800	2200	2100	1700	2300	1885	1975	2035	2172
R1, Oм	100	90	105	95,8	97,2	107,3	88,8	94,2	103,8	104,5
С0, мкФ	0,1	0,05	0,1	0,05	0,1	0,05	0,1	0,05	0,1	0.05
r0, Ом	100	80	120	90	60	75	95	110	117	85
f, Гц	100	400	500	1000	500	400	100	1000	400	600

4.3 Измерение индуктивности

Задача 4.3

Для измерения применён четырёхплечий мост переменного тока (рисунок 4.3)

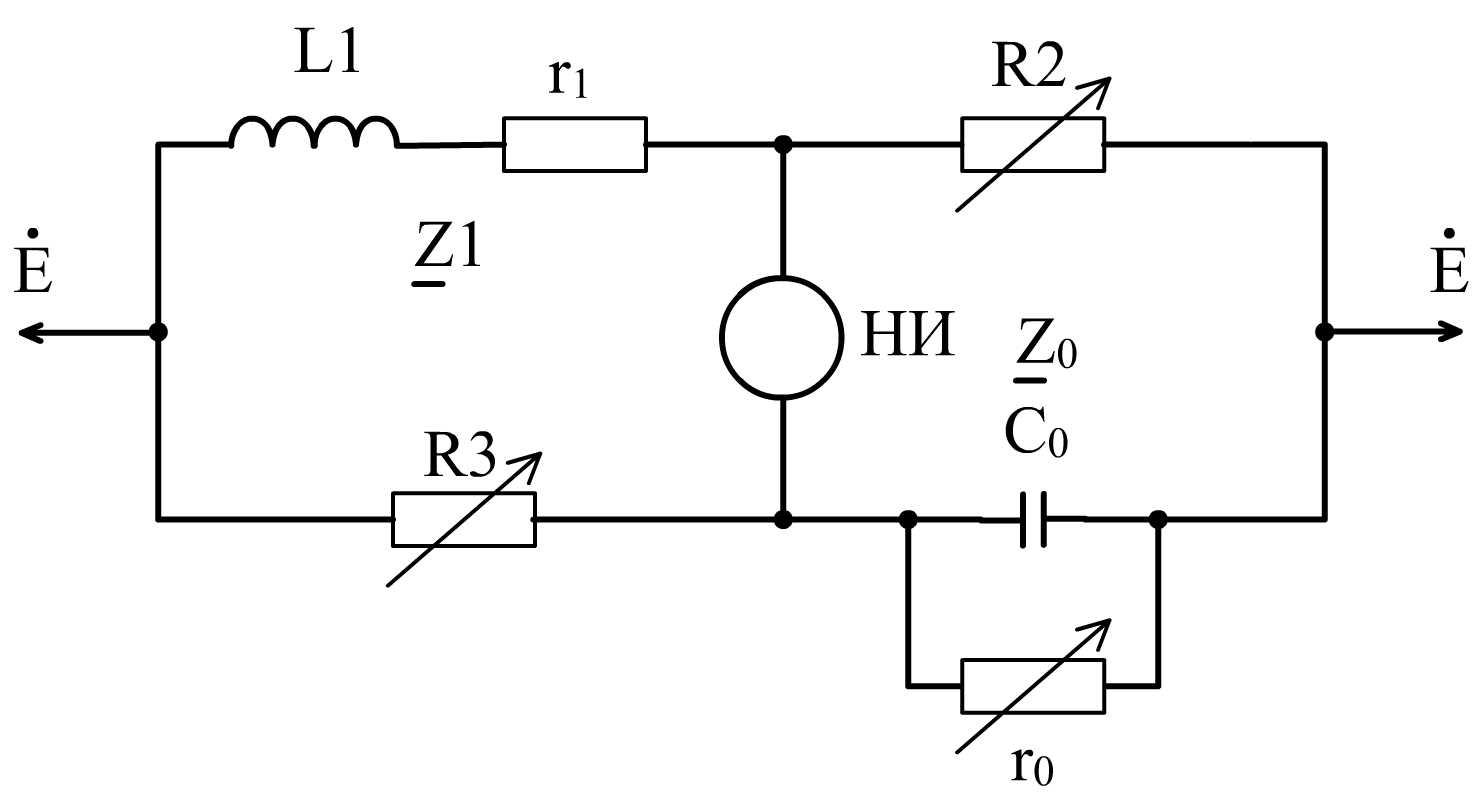
Рисунок 4.3 – Схема моста для измерения индуктивности с использованием образцовой ёмкости

Найдите:

а) Значение индуктивности;

б) Значение сопротивления катушки индуктивности и её добротность.

Руководство к выполнению

Равновесие моста наступает при выполнении условия

Z₁Z₀ = R₂R₃, (4.7)

где Z₁ = r₁ + jωL₁;

Z₀ = R₀/ (1 + jωС₀r₀) (4.8)

После преобразования получим

r₁r₀ + jωL₁r₀ = R₁R₂ + jωС₀r₀R₁R₂ (4.9)

Из (4.9) получим два рабочих уравнения баланса моста

r₁ = R₁R₂/r₀; (4.10)

L₁ = C₀R₁R₂. (4.11)

Добротность катушки равна

Q = ωL₁/r₁ = ωC₀r₀ (4.12)

Для того чтобы добротность можно было бы отсчитывать по шкале положения ручки переменного резистора r₀, надо обеспечить

С₀ = 0,1 мкФ, ω = 2πf = 6,28 · 10³.

Таблица 4.3

Параметры мостовой цепи	Вариант, последняя цифра шифра
	0	1	2	3		4	5		6		7		8	9
R2, Ом	100	120	98,3		115	88		97	99	105		103		102
R3, Ом	100	105	103,2		108	101		104,5	98	101		102		100
r0, кОм	1	0,8	1,2		1,3	1,05		1,4	1,1	1,17		1,15		0,9