Содержание

  

Введение……………………………………………………...………………...3

2. Задание 2

К шинам РУ 6-10 промышленного предприятия присоединены N синхронных электродвигателей, требуется с помощью метода неопределенных множителей Лагранжа определить оптимальную реактивную мощность от каждого из синхронных двигателей, пренебрегая сопротивлениями кабелей. Реактивная нагрузка, подлежащая компенсации на стороне 6-10 кВ, определяется вариантом задачи. Данные к задаче для каждого из вариантов принимаются по таблицам 2.1, 2.2 и 2.3. Технические характеристики двигателей приведены в таблице 2.4.……………………………..……………………………………………...6

3. Задание 3

От шин низкого напряжения (рисунок 3.1) цеховой трансформаторной подстанции (ТП) питаются три группы электродвигателей (n₁, n₂, n₃) с потребляемой мощностью n₁ х S₁, n₂хS₂, n₂хS₃ (таблица 3.1) и одинаковым Cosj = 0,85. Вероятность включения в работу каждого двигателя первой группы - p₁, второй группы - p₂, третьей группы - p₃ (таблица 3.2). События включения в работу и отключения любого двигателя каждой группы рассматриваются как независимые. Показатели надежности элементов системы электроснабжения приведены в таблицах 3.4 и 3.5, данные системы электроснабжения в таблице 3.3.……………………………………………………...……………………………..10

Заключение……………….…………………...……………………………….17

Список использованной литературы…….…..…………...….………………18

Введение

Данная расчетно-графическая работа предназначена для закрепления теоретического материала, пройденного на лекционных и практических занятиях.

Расчетно-графическая работа включает в себя 3 задания.

В первом задании нужно решить систему линейных уравнений графическим методом. Также нужно построить область допустимых решений и определить точку экстремума функции.

Во втором требуется с помощью метода неопределенных множителей Лагранжа определить оптимальную реактивную мощность от каждого из синхронных двигателей, пренебрегая сопротивлениями кабелей. Реактивная нагрузка, подлежащая компенсации на стороне 6-10 кВ, определяется вариантом задачи. Данные к задаче для каждого из вариантов принимаются по таблицам 2.1, 2.2 и 2.3. Технические характеристики двигателей приведены в таблице 2.4

А в третьем задании от шин низкого напряжения (рисунок 3.1) цеховой трансформаторной подстанции (ТП) питаются три группы электродвигателей (n₁, n₂, n₃) с потребляемой мощностью n₁ х S₁, n₂хS₂, n₂хS₃ (таблица 3.1) и одинаковым Cosj = 0,85. Вероятность включения в работу каждого двигателя первой группы - p₁, второй группы - p₂, третьей группы - p₃ (таблица 3.2). События включения в работу и отключения любого двигателя каждой группы рассматриваются как независимые. Показатели надежности элементов системы электроснабжения приведены в таблицах 3.4 и 3.5, данные системы электроснабжения в таблице 3.3.

Задание 2.

К шинам РУ 6-10 промышленного предприятия присоединены N синхронных электродвигателей, требуется с помощью метода неопределенных множителей Лагранжа определить оптимальную реактивную мощность от каждого из синхронных двигателей, пренебрегая сопротивлениями кабелей. Реактивная нагрузка, подлежащая компенсации на стороне 6-10 кВ, определяется вариантом задачи. Данные к задаче для каждого из вариантов принимаются по таблицам 2.1, 2.2 и 2.3. Технические характеристики двигателей приведены в таблице 2.4.

Дано:

4	6	6300	1000	750	600	500	70	1,6

	1000	3,15	14,6	13,1
	750	3,15	18,1	14,8
	600	3,15	17,1	14,4
	500	3,16	21,0	16,3

Решение:

1) Определим максимальную реактивную мощность, который можно получит от синхронного двигателя:

(2.1)

где, α_m – коэффициент учитывающий максимальную реактивную мощность (α_m=1.39=const);

M – количество двигателей, имеющих одинаковую мощность и скорость вращения (М=1);

Q_H – номинальная реактивная мощность.

Подставляем числовые данные:

1,39*1*3,15=4,3785 МВар;

= 1,39*1*3,15=4,3785 МВар;

1,39*1*3,15=4,3785 МВар;

1.39*1*3,16=4,3924 МВар;

2) Определим составляющие затраты на генерацию двигателями реактивной мощности:

(2.2)

(2.3)

где, С₀ – удельная стоимость, у.е./кВт;

Д₁, Д₂ – составляющее затраты по мощности, кВт;

Q_Hi – номинальная реактивная мощность, МВар;

M – количество двигателей, имеющих одинаковую мощность и скорость вращения (М=1);

у.е./МВАр;

у.е./МВАр;

у.е./МВАр;

у.е./МВАр;

;

З ;

З ;

З

3) Составим функцию Лагранжа:

(2.4)

4) Определим неопределенный множитель Лагранжа:

(2.5)

где, Q_A – мощность подлежащее компенсации;

З_1i, З_2i – затраты на генерацию двигателями реактивной мощности.

5) Определим оптимальную реактивную мощность от каждого синхронного двигателя:

(2.6)

где, - множитель Лагранжа;

З_1i, З_2i – затраты на генерацию двигателями реактивной мощности.

=

6) Правильность расчетов определяем по балансу реактивной мощности:

(2.7)

_{По вычисленным формулам я убедился в правильности выполненных расчетов:}

Задание 3.

От шин низкого напряжения (рисунок 3.1) цеховой трансформаторной подстанции (ТП) питаются три группы электродвигателей (n₁, n₂, n₃) с потребляемой мощностью n₁ х S₁, n₂хS₂, n₂хS₃ (таблица 3.1) и одинаковым Cosj = 0,85. Вероятность включения в работу каждого двигателя первой группы - p₁, второй группы - p₂, третьей группы - p₃ (таблица 3.2). События включения в работу и отключения любого двигателя каждой группы рассматриваются как независимые. Показатели надежности элементов системы электроснабжения приведены в таблицах 3.4 и 3.5, данные системы электроснабжения в таблице 3.3.

Требуется определить:

а) вероятность нагрузки трансформаторов питающей подстанции (ТП) на:

1) S₁ = 0 кВА;

2) S₂ = 60 кВА;

3) S₃ = 100 кВА;

4) на величину максимальной мощности потребителя;

б) математическое ожидание, дисперсию, среднеквадратичное отклонение случайной величины нагрузки трансформатора;

в) определить показатели надежности системы электроснабжения, представленной на рисунке 3.1, относительно шин 0,4 кВ (без учета преднамеренных отключений):

1) интенсивность отказов l_с, 1/г;

2) среднее время восстановления t_авс, час;

3) среднюю наработку на отказ Т_с, лет;

4) коэффициент простоя g_с, коэффициент готовности р_с.

г) Определить величину недоотпущенной электроэнергии за год (8760 ч.) относительно шин 0,4 кВ.

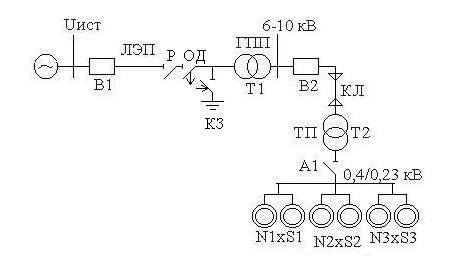
Рисунок 3.1 – Схема электроснабжения

Дано:

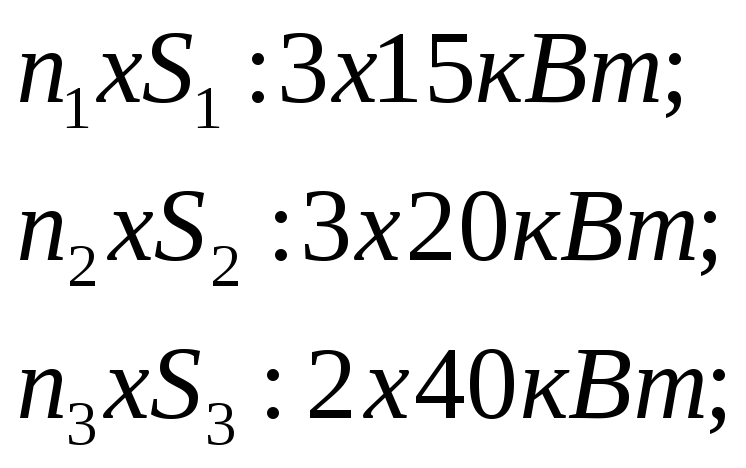
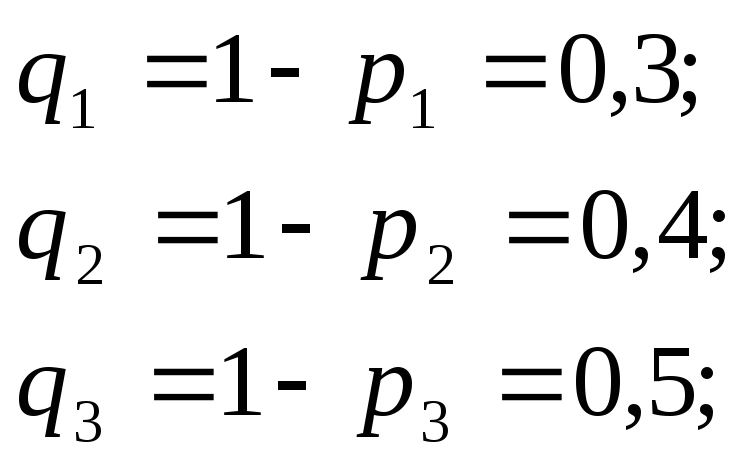
Решение:

1. Определим вероятность нагрузки трансформаторов цеховой

трансформаторной подстанции (ТП).

Для определения вероятностей заданной нагрузки трансформатора используется схема независимых испытаний – биномиальный закон распределения:

; (3.1)

где, n – число независимых испытаний;

к – число испытаний, в которых событие А появилось из серии n независимых испытаний;

р – вероятность включения двигателя;

g – вероятность отключения двигателя.

а) S₁ = 0 кВА

При S₁ = 0 кВА имеем 1 вариант включения двигателей:

_{(0×15)(0×20)(0×40)}

б) S₂ = 60 кВА

При S₂ = 60 кВА имеем 2 варианта включения двигателей:

1)(0×15)(1×20)(1×40) 2) (0×15)(3×20)(0×40)

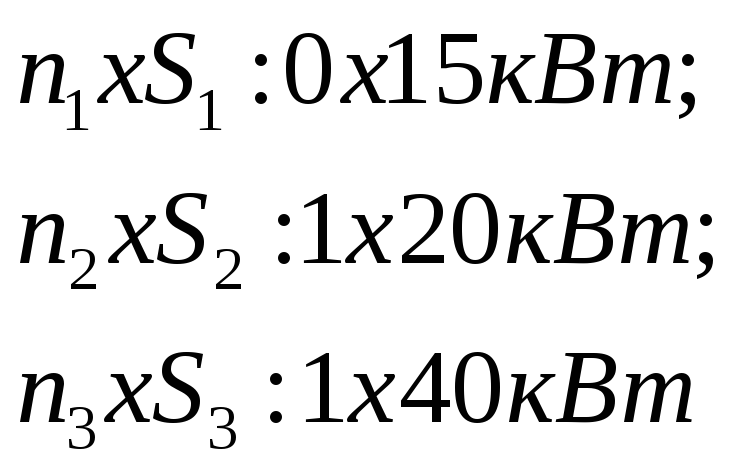
1)

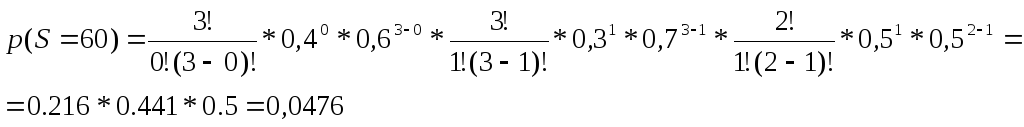
₂₎

в) S₃ = 100 кВА

При S₃ = 100 кВА имеем 2 варианта включения двигателей:

1) (0×15)(1×20)(2×40) 2) (0×15)(3×20)(1×40)

₂₎

г) S₄ = 185 кВА (максимальное значение)

При S₄ = 185 кВА имеем 1 вариант включения двигателей:

1. (3×15)(3×20)(2×40)

1)

2. Определение математического ожидания, дисперсии, среднеквадратичного отклонения случайной величины нагрузки трансформатора.

Математическое ожидание:

(3.2)

где, n_i – число i-го независимого испытания;

р_i – вероятность i-го включения двигателя;

S_i – мощность i-го потребителя.

Дисперсия:

_(3.3)

где, n_i – число i-го независимого испытания;

р_i – вероятность i-го включения двигателя;

S_i – мощность i-го потребителя.

Среднеквадратичное отклонение:

(3.4)

_{где, D(S) – дисперсия}

кВА²