
На сортировку / 2 / Конспект(итог)1
.doc|
1 Основные понятия о трехфазных источников и трехфазных цепях И
З
Рассмотренная система ЭДС наз. симметричной 3-хфазной системой ЭДС. Условие симметричной системы: одинаковая амплитуда, частота и одинаковый фазовый сдвиг на 120 град.При нарушении одного из усл. система несимметрична |
5 Мощность трехфазной цепи в симметричном режиме В симметричном режиме мощности потребляемые в фазах одинаковы, поэтому мощность 3-х фазной цепи равна утроенной мощности одной фазы. Для
активной мощности, мощность 3-х фазной
цепи равна
Выразим фазные напр.и токи через линейные Для
звезды
|
|
2 Р Провод
Nn-нейтральный
или нулевой провод, тогда схема
обозначается
Напряжения
и токи на фазах генератора и нагрузки
наз.фазными напряжениям и токами
генератора и нагрузки
Соединительные
провода
Линейные фазные токи в схеме звезды одинаковы. Т Напряжение м/у линейными проводами наз. линейными напряжениями:
Рассмотрим схему треугольника, при этом конец обмотки (фазы) соединяется с нач. B, а кон. с нач. С. Линейные токи Фазные токи нагрузки
|
6 Рассмотрим 3-хф цепь, в к-ой есть нагрузки соед звездой и треугольником Генераторы нагрузки симметричны
Симметричный
генератор можно представить схемой
с тремя ист. фазных ЭДС
Для
расчета целесообразно 3-уг с сопр.
В В полученной схеме можно выделить все, что относится к фазе А и получить однофазную схему Рассчитываем
токи
Для
расчета Iф
в треугольнике используют соотношения
для симм-ых режимов: |
|
3 Симметричный режим трехфазной цепи соединенной звездой Наз. режим, когда к симметричному генератору подключена симметричная нагрузка Нагрузка наз. симметричной, если даны комплексные сопротивления всех фаз Активно индуктивный характер В симметр. режиме токи образуют симметрич систему токов, а в нейтрали они отсутстств
|
7 Расчет несимметричных режимов 3-х цепи со стат. нагрузкой Рассматриваем стат. нагрузку, т.е. нагрузку не содержащую двигателей Пренебрегаем внутренним сопротивлением генератора. При этом генератор представляется с помощью ист. ЭДС а) Расчет несимметричного режима в схеме соединенной звездой с нейтральным проводом
Если заданы фазные напр. генератора, то можно считать их принадлежащими 3-м ист. и представить ген. в симметрич. схеме П Затем токи в фазах и ток в нейтральном проводе рассчитываем по закону Ома
Обрыв нейтрали
Токи
рассчитываются также, а ток в нейтрали
будет равен 0
|
|
4 Симметричный режим трехфазной цепи соединенной треугольником
Р
В симметричном режиме трехфазные токи образуют симметричную 3-х фазную систему токов. Линейные токи выражаются по первому закону Кирхгофа через ф. токи
Линейные ЭДС построим из одной точки со сдвигом на 120 градусов Для симметричного режима:
|
б) Расчет несимметричного режима в схеме звезды без нейтрального провода П включены
в фазы В и С
в Для расчета целесообразно заменить треугольник сопротивлений эквивалентной звездой и рассчитать линейные токи по рассмотренной ранее методикой
Д
Фазные
токи по закону Ома
|
|
8 Рассмотрим схему, в которой есть нагрузки соединенные звездой и треугольником В данном случае целесообразно звезду заменить эквивалентным треугольником. После чего получим два треугольника, соединенных параллельно и можем объединить их в один треугольник. Получим схему рассмотренную в предыдущем параграфе
Н |
11 Линейные диаграммы в трехфазных цепях Р П т.D–
х.х..т.А- к.з. т.n-
сим.
режим
При
изм.
|
|
9 Аварийные режимы в 3-х фазных цепях Аварийный режим возникает при обрыве линейного или фазного проводов, также при коротком замыкании на нагрузке или в линии Рассмотрим различные схемы а) а.р в схеме звезда с нейтральным проводом: В О
В результате обрыва в фазах В и С токи не изменяются, но возник ток в нейтрале равный по величине фазному току П б) а.р в 3-х ф. цепи соединенной звездой без нейтрального провода Диаграмма такая же. в) обрыв линейного провода Н
г) К. з. в одной из фаз нагрузки. П Напр.
в фазе В и С становятся равными лин.
напр., т.е. увеличивается в
|
12 Круговые диаграммы в 3-хф. цепях П Запишем
выражение для
При
изменении
П 1 напряжений и проводим диаметр AD 2. Из точки А по линии AD откладываем неизменную проводимость 2g бранном масштабе проводимости mg. 3.
Из точки F
под
4.
Из начала точки А опускаем
Для разметки фаз можно исп. Простую схему, к которой вкл. 2 лампочки и один конденсатор, соед. звездой
|
|
10 Аварийные режимы в схеме треугольника
Обрыв линии А
Напр.
на фазах ab
и ca
стали равны половине напр.
При
обрыве фазы |
14 Сопоставление схем 3-хф цепей применяемым при питании одноф. потребителей П Сопоставим схему звезда с нейтральным проводом и треугольник при обрыве одной из фаз. При обрыве одной из линий в схеме звезды с нейтральным проводом под нормальным напр. остается 2 группы потреб., тогда как в схеме треуг-ка под нормальным напр. ост. 1 группа. Поэтому надежней явл. Схема звезда с нейтральным пр. В схеме с нейтральным пр. обеспечивается 2 ур. напр. фазное и линейное. Т.о. при питании одноф. потреб. прим. схема звезда с нейтральным пр. |
|
13 Изменение мощности в 3-хф. цепях Активная мощность измеряется с помощью ваттметра. В симм. Режиме достаточно одного ваттметра, измеряющего активную мощность фазы
В несимм. режиме при наличии нейтрального провода исп. 3 ваттметра
При
отсутствии нейтрального провода
обычно исп. схема двух ваттметров,
вкл.. в любые две фазы. Например:
Покажем, что сумма показаний ваттметра дает активную мощность, потребляемую всей цепью.
Т.о. сумма показаний двух ваттметров дает активную м. всей цепи.
|
15 Вращающееся магнитное поле Синусоидальный ток создает пульсир. магн. поле, в к-ой вектор магн. индукции оставаясь неизменным по напр. изм. по величине по синусоидальному закону.
Т Круговое вращ. магн. поле позволяет осуществить создание асинхронного 3-хф. двигателя.
|
|
16 Метод симм. составляющих М.с. сост. основан на представлении несимм. 3-хф системы величин в виде суммы 3-х симм. 3-хф. систем. Расчет проводится отдельно для каждой симм. системы и получ. результаты суммируются Сущ.3 симм. системы: 1.Симм. система с нулевой последовательностью. 2. Симм. система обратной последовательности 3. Симм. система прямой последовательности С |
18 Расчет цепи в несимм. нагр. методом симм. составляющих Р Для расчета заданы:
Вместо
несимм. нагр. в каждую фазу вкл. источники
с напр.
К
Н Составляем расчетные схемы прямой, обратной и нулевой посл. для фазы А: Схемы
прямой, обр. и нулевой послед.
целесообразно упростить, заменив две
параллельные ветви одной эквивалентной.
При этом не трогаем ветви с неизвестными
ист.
Получаем схему с 6 ур. с 6 неизвестными, решая к-ые находим симм. сост. напр. и токов в месте подключения несимм. нагрузки:
|
|
17 Расчет токов в несимм. нагрузке Если в несимм . нагр. приложить симм. систему напр., то в цепи возникнет несимм. система токов, к-ая содержит симм. сост. прямой, обратной и нулевой последовательностей. Следовательно в несимм. нагр симм. система токов и напр. различных послед. зависят друг от друга. Поэтому невозможно составить расчетные схемы для каждой из последовательности в отдельности. Для расчета прим. теорема о компенсации, с помощью к-ой несимм. нагр. заменяется источниками напр., вкл. в каждую фазу. В электроэнергетике несимм. режимы возникают при к.з или обрывах линейных проводов. Различают поперечную и продольную несимм. |
19 Расчет цепи с несимм. уч. линии методом симм. сост. Н С Для каждой схемы сост. ур. по 2 закону Кирхгофа и три доп. ур. по заданной схеме несимм. участка
|
|
1 Разложение несинусоидальной кривой в тригонометрический ряд Любая
периодич. несинусоид. ф-ия
|
2 Особенности разложения в ряд некоторых ф-ии, облад-их симметрией 1 Ф-ии симм. относительно оси абсцисс
При разложении в ряд формы (1) такие ф-ии не содержат пост. составляющих и всех четных гармоник
2 Ф-ии симм. относительно оси ординат
При разложении в ряд формы (2) эти ф-ии не содержат синусоид. ряд
3 Ф-ии симм. относительно начала координат
При разложении в ряд ф-ии (3) не содержит пост. сост. и косинусный ряд
|
|
3 Действующие и ср. значения несинусоидальных ЭДС, напр. и токов Любая несинусоидальная кривая характеризуется 3-мя величинами: 1 Амплитуда или максимальное значение за период. 2 Действующее значение ф-ии за период
3 Среднее значение за период
Запишем выражение для действующего значения несин-ых ф-ий через отдельные гармоники:
После вычисления получим, что действ. значение ф. равно корню квадратному из суммы квадратов действующих значений отдельных гармоник
Пример:
Действующее значение этого напр. равно:
|
4 Коэффициенты, характеризующие форму несинусоидальных периодических кривых Для оценки степени отличия формы несинусоидальной кривой от синусоиды исп. ряд коэф-ов. Рассмотрим их: 1 Коэффициент формы равен отношению действ. значения к среднему по модулю значению
3
Коэф. искажения равен действующему
значению 1-ой гармоники к действующему
значению всей кривой 4Коэф. гармоники равен отношению действующих значений всех высших гармоник к действующему значению1-ой гармоники
|
|
5 Мощности в цепях несинусоидального тока
Аналогично
опр. реактивная мощность. Реактивная
м. равна сумме реактивных м. отдельных
гармоник
В
цепях несин. тока возникает м. искажения
Т, к-ая обусловлена различием форм
кривых напр. и тока |
6 Расчет цепей несинусоидального тока Расчет проводится в три основных этапа: 1 Зад. ЭДС или ток ист. расклад. в триг. ряд и представ. в виде суммы гармоник 2 Проводится расчет заданной цепи для к-ой из гармоник в отдельности 3 Результ., получ. для к-ой гарм. обобщаются и наход. несин токи и напр. в цепи 1 Разложение в ряд производится исходя из заданной степени точности апроксилации (мат. описание) несин. кривой, поэтому в разложении в ряд оставляется конечное число гармоник. 2 На втором этапе производится расчет схемы n раз для к-ой гармоники
Необходимо
учитывать зависимость реактивных
сопр. L
и
Cот
частоты
|
|
7 Высшие гармоники в трехфазных цепях Представим
трехфазный генератор с несин. ЭДС и
запишем выражение к-ой гармоник для
3-х фаз
Рассмотрим
особенности,
к-ые возник. в 3-хф. цепях 1
Линейные напр. не содержат гарм. с ном.
кратным 3-ем при наличии этих гармоник
в составе фазного напр.
3 При отсутствии нейтрального тока м/у ген. и нагр. появл. напр. сост. из гарм. с ном. кр. 3-ем. Даже в симм. режиме Смещение нейтрали для 3-ей гарм. в симм. режиме
4
В схеме треугольника при разомкнутых
обмотках
Гарм. сном. кр. 3-ем сумм.. и ваттметр покажет напр. сост. из гармоник с ном. кр.3-ем 5
В замкнутом
треуг. обмоток ген. протек. токи всех
гармоник, поэтому ф-ой ток генератора
равен
|
1 Основные ур. пассивного четырехполюсника 1-1-входные или первичные зажимы 2-2-выходные или вторичные зажимы Схема
прямого питания
Выведем осн. ур., связывающие напр. и токи на входе и выходе четырехполюсника: 1Нагрузку
2Токи
Четырехполюсник
наз. симм., если у него равны A=D,
т.е при перестановке.U
и
I
на входе и выходе не меняются
|
|
4 Частотные электрические фильтры Фильтр- четырехполюсник, к-ый вкл. между источником и приемником и служит для выделения из всего спектра частот ист. одной или нескольких обл. частот Принцип работы фильтров осн. на зависимости реактивных сопр. L и C от частоты. Будем рассматривать идеальные фильтры сост. из чисто реактивных сопр. (элементов). Ф
Осн. хар-ками ф. явл. зависимость а и в от частоты. Обл. пропускания наз. обл. частот, в к-ой Коэф. затух а =0. Обл. частот, в к-ых Коэф. затух. а>0 наз. обл. затухания ( непропускания )
|
5 Низкочастотные фильтры
Найдем
граничные частоты обл. пропускания В
полосе затухания коэф. фазы неизменен
и равен
Построим графики зависимости коэф. затухания от частоты: |
|
5 Высокочастотные фильтры
Коэф.
b
в полосе пропуск.
|
2 Определение коэф. четырехполюсника Коэф.
A
и
D
– безразмерные Коэф. ч-ка можно либо
рассчитать, либо найти экспериментальным
путем. Проще всего коэф. опр-ся из
режимов х.х. и к.з. 1 |
|
6 Полосовые и заграждающие фильтры Полосовой фильтр можно получить посл. соединением НЧ и ВЧ ф. или объединить их элементы Заграждающие ф. получ. параллельным соед. НЧ и ВЧ фильтров |
|
|
3 Схемы замещения симм. четырехполюсника Основные схемы замещения это Т и П Т-образная схема П-образная схема
Т и П –схемы будут явл. схемами замещения, если равны соответствующие коэф. заданного четырехполюсника и его схемы замещения Рассчитаем
параметры Т-схемы, т.е.
|
|
|
|
|

 сточником
3-хфазной системы напряжений является
синхронный генератор.
сточником
3-хфазной системы напряжений является
синхронный генератор. 
 Синхронный
генератор имеет неподвижную часть
статор, на котором расположены 3
обмотки, сдвинутые в пространстве на
120 градусов и подвижную часть ротор,
на котором расположена система
электромагнитов, создающих магнитное
поле. При вращении ротора магнитные
силовые линии пересекают обмотки
статора и в каждой из них индуцируется
ЭДС. Т.о. получаем трехфазную систему
ЭДС с одинаковой частотой и амплитудой
сдвинутые др. относ друга на 120градксов
Синхронный
генератор имеет неподвижную часть
статор, на котором расположены 3
обмотки, сдвинутые в пространстве на
120 градусов и подвижную часть ротор,
на котором расположена система
электромагнитов, создающих магнитное
поле. При вращении ротора магнитные
силовые линии пересекают обмотки
статора и в каждой из них индуцируется
ЭДС. Т.о. получаем трехфазную систему
ЭДС с одинаковой частотой и амплитудой
сдвинутые др. относ друга на 120градксов апишем
3-хфазную систему ЭДС в комплексной
форме
апишем
3-хфазную систему ЭДС в комплексной
форме
 Схемы соединения трехфазных цепей
звездой и треугольником
Схемы соединения трехфазных цепей
звездой и треугольником
 ассмотрим
схему звезды, при этом концы обмоток
генератора x,
y,
z
соединяются в одну точку, к-ая наз
нейтральной или нулевой точкой
генератора
ассмотрим
схему звезды, при этом концы обмоток
генератора x,
y,
z
соединяются в одну точку, к-ая наз
нейтральной или нулевой точкой
генератора
 ок
в нейтральном проводе наз. нейтральным
или нулевым. Он направлен от нагрузки
генератора.
ок
в нейтральном проводе наз. нейтральным
или нулевым. Он направлен от нагрузки
генератора.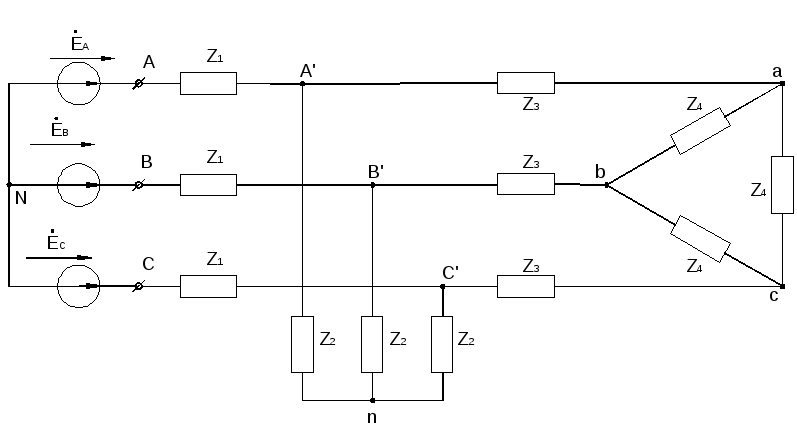 Расчет симметрич. Режимов разве. трех.
цепей
Расчет симметрич. Режимов разве. трех.
цепей

 симметричном режиме нейтральные точки
ген. N
и
нагр.
симметричном режиме нейтральные точки
ген. N
и
нагр.

 ,
,

 рименим
для расчета этой схемы метод 2-х узлов,
в соответствии с которым рассчитываем
напр. м/у нейтральными точками ген. и
нагрузкой
рименим
для расчета этой схемы метод 2-х узлов,
в соответствии с которым рассчитываем
напр. м/у нейтральными точками ген. и
нагрузкой

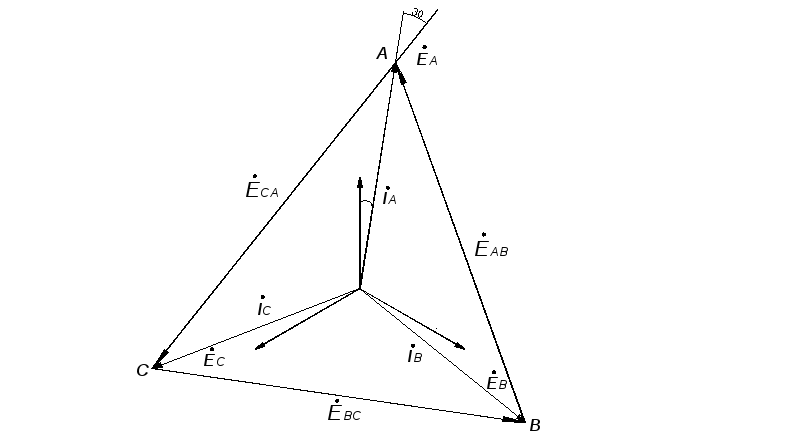 ассчитываем
фазные токи
ассчитываем
фазные токи ри
отсутствии нейтрального провода
задаются обычно линейные напряжения
ген.и их сумма равна0
ри
отсутствии нейтрального провода
задаются обычно линейные напряжения
ген.и их сумма равна0
 )
Расчет несимметричного режима в схеме
треугольника
)
Расчет несимметричного режима в схеме
треугольника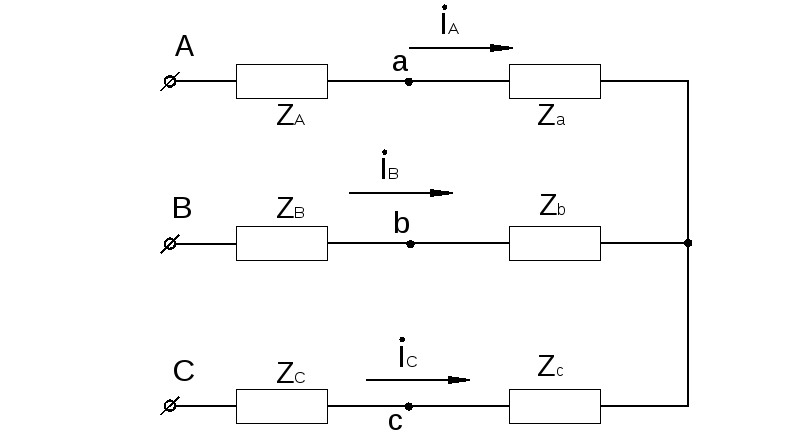 ля
расчета фазных токов в исходной схеме
треугольника необходимо найти линейное
напряжение м/у вершинами треугольника
ля
расчета фазных токов в исходной схеме
треугольника необходимо найти линейное
напряжение м/у вершинами треугольника
 Расчет несимметричных режимов
разветвленных трехфазных цепей
Расчет несимметричных режимов
разветвленных трехфазных цепей
 аходим
через линейные токи напряжения м/у
точками а, в, с
аходим
через линейные токи напряжения м/у
точками а, в, с
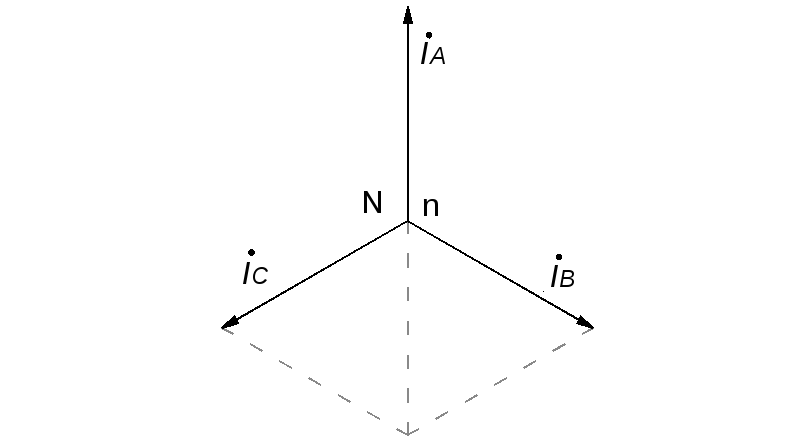
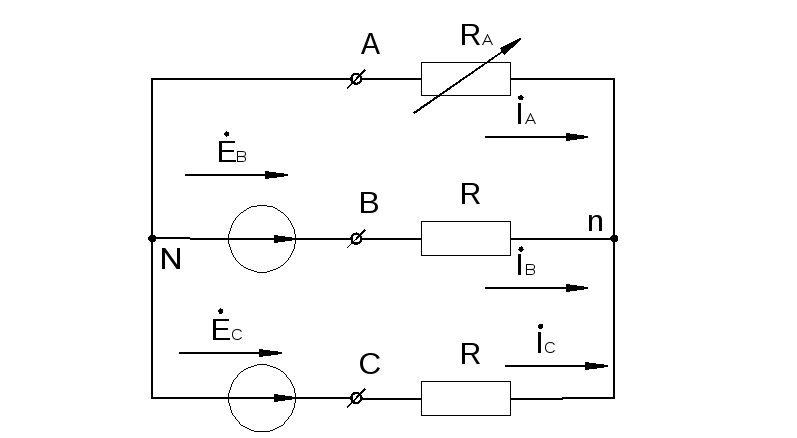 ассмотрим
3-хф. цепь, соединенной звездой без
нейтрального провода. Представим ген.
эквивалентной схемой с двумя ист. ЭДС,
вкл. В фазы В и С
ассмотрим
3-хф. цепь, соединенной звездой без
нейтрального провода. Представим ген.
эквивалентной схемой с двумя ист. ЭДС,
вкл. В фазы В и С

 оделим
числитель и знаменатель 2g
оделим
числитель и знаменатель 2g
 симметричном режиме токи образуют
симметрич. систему токов и ток в
нейтральном проводе равен 0
симметричном режиме токи образуют
симметрич. систему токов и ток в
нейтральном проводе равен 0
 ри
к. з. одной из фаз нагрузки ток в этой
фазе будет ограничиваться только
внутренним сопротивлением ген. и может
достигнуть недопустимых величин,
ри
к. з. одной из фаз нагрузки ток в этой
фазе будет ограничиваться только
внутренним сопротивлением ген. и может
достигнуть недопустимых величин, апример
линии А
апример
линии А


 ри
к. з в фазе А потенциал нейтральной
точки нагузки
n
становится равным точки А.
ри
к. з в фазе А потенциал нейтральной
точки нагузки
n
становится равным точки А.
 олуч.
при неоднородных нагр.
олуч.
при неоднородных нагр.

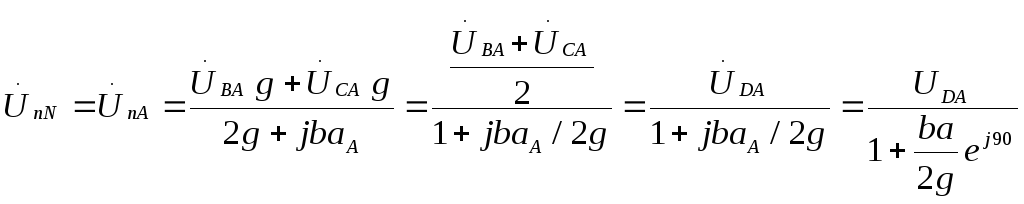
 орядок
построения круговой диаграммы:
орядок
построения круговой диаграммы: .
Строим треугольник линейных
.
Строим треугольник линейных




 ри
питании одноф. потребителей необходимо
обеспечить номинальную величину напр.
на зажимах потреб. независимо от вкл.
нагрузки. Данному требованию удовл.
Схема звезда с нейтральным проводом
и схема
ри
питании одноф. потребителей необходимо
обеспечить номинальную величину напр.
на зажимах потреб. независимо от вкл.
нагрузки. Данному требованию удовл.
Схема звезда с нейтральным проводом
и схема



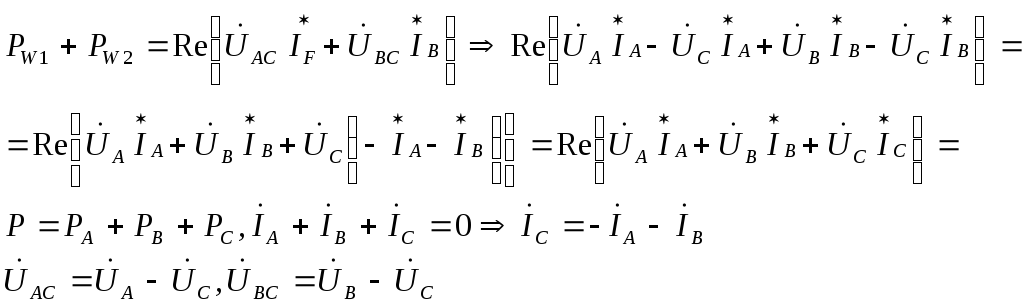




 Вычислим величину
суммарного вектора магн. индукции для
различных моментов времени
Вычислим величину
суммарного вектора магн. индукции для
различных моментов времени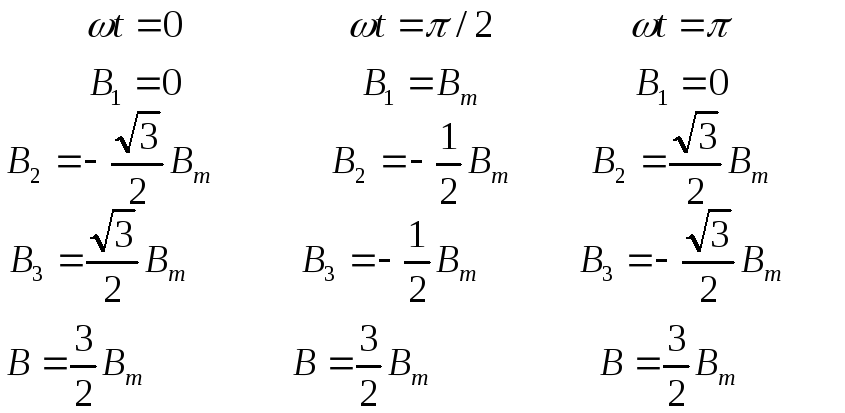 .о.
симм. система токов создает круговое
вращающееся магн. поле, т.е. вектор
магн. инд. остается неизменным по
величине и вращается с уг. ск-ю равной
уг. частоте, т.е. за один период совершает
один оборот.
.о.
симм. система токов создает круговое
вращающееся магн. поле, т.е. вектор
магн. инд. остается неизменным по
величине и вращается с уг. ск-ю равной
уг. частоте, т.е. за один период совершает
один оборот. имм.
система прямой последовательности-
это 3 вектора одинаковой величины
сдвинутые др. относ. др. на 120 град. с
прямой последовательностью чередования
фаз ABC.
имм.
система прямой последовательности-
это 3 вектора одинаковой величины
сдвинутые др. относ. др. на 120 град. с
прямой последовательностью чередования
фаз ABC. Симм.
система обратной последовательности
– это 3 вектора сдвинутые др. относ.
др. на 120 град. с обратной посл. чередования
фаз.
Симм.
система обратной последовательности
– это 3 вектора сдвинутые др. относ.
др. на 120 град. с обратной посл. чередования
фаз. Симм. система с нулевой последовательностью-
это 3 одинаковых вектора
Симм. система с нулевой последовательностью-
это 3 одинаковых вектора
 ассмотрим
цепь, в которой симм. ген. через линию
питает симм. динамичную нагр. и несимм.
статич. нагр.
ассмотрим
цепь, в которой симм. ген. через линию
питает симм. динамичную нагр. и несимм.
статич. нагр. аждые
из этих напр. раскладываем на симм.
составляющие:
аждые
из этих напр. раскладываем на симм.
составляющие:

 апр.
ист. противоположно напр. токов
апр.
ист. противоположно напр. токов
 Составим
систему ур. по 2 закону Кирхгофа для
получ. простейших схем и доп. три ур.
на основе заданной конкретной схемы
несимм. нагркзки. Наиболее распр.
случай несимметрии это однофазное
к.з. Напр. А
Составим
систему ур. по 2 закону Кирхгофа для
получ. простейших схем и доп. три ур.
на основе заданной конкретной схемы
несимм. нагркзки. Наиболее распр.
случай несимметрии это однофазное
к.з. Напр. А

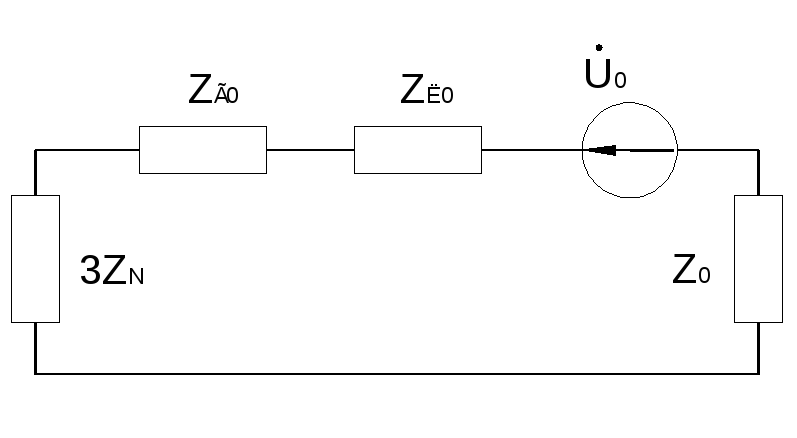
 есимм.
участок заменяем тремя источниками
с напр.
есимм.
участок заменяем тремя источниками
с напр.

 ост.
эквивалентные схемы прямой, обратной
и нулевой последовательности:
ост.
эквивалентные схемы прямой, обратной
и нулевой последовательности:




 2
Коэф. амплитуды равен отношению
максимального значения к действующему
значению
2
Коэф. амплитуды равен отношению
максимального значения к действующему
значению


 Р
– среднее значение мгновенной мощности
р за период
Р
– среднее значение мгновенной мощности
р за период Активная
мощность несинусоидального тока равна
сумме активных мощностей отдельных
гармоник
Активная
мощность несинусоидального тока равна
сумме активных мощностей отдельных
гармоник Полная
м. несин. тока равна произведению
действ. зн. несин. напр. и несин. тока
Полная
м. несин. тока равна произведению
действ. зн. несин. напр. и несин. тока



 В составе тока индуктивности L
%-ое содержание высших гармоник меньше,
чем в составе приложенного напряжения
В составе тока индуктивности L
%-ое содержание высших гармоник меньше,
чем в составе приложенного напряжения
 Для С %-ое содержание высших гармоник
в составе тока больше, чем в составе
приложенного напряжения
Для С %-ое содержание высших гармоник
в составе тока больше, чем в составе
приложенного напряжения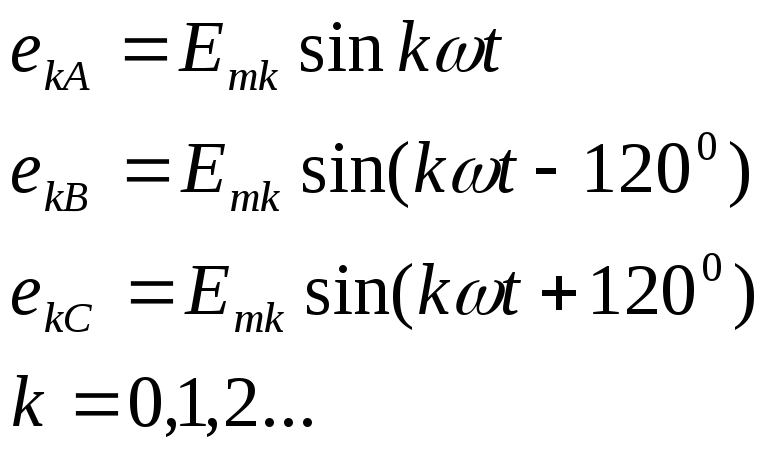 Если
k=2,
то получим обратную послед. Если к=3,
то нулевая последовательность Если
к=4, то прямая К=5, обратная Гармоники
с номерами к = 3n+1,
где n-это
числа натурального ряда, образ. симм.
систему прямой послед. Гармоники с
номерами к=3n+2,
образ. систему обр. послед. Кривые,
исп. в эл.энергетике не содержат четных
гармоник, поэтому во внимание принимаем
только нечетные гарм.
Если
k=2,
то получим обратную послед. Если к=3,
то нулевая последовательность Если
к=4, то прямая К=5, обратная Гармоники
с номерами к = 3n+1,
где n-это
числа натурального ряда, образ. симм.
систему прямой послед. Гармоники с
номерами к=3n+2,
образ. систему обр. послед. Кривые,
исп. в эл.энергетике не содержат четных
гармоник, поэтому во внимание принимаем
только нечетные гарм. 2 Ток
в нейтральном проводе равен утроенной
величине тока нулевой посл., т.е. гарм.
с ном. кр.3-ем.
2 Ток
в нейтральном проводе равен утроенной
величине тока нулевой посл., т.е. гарм.
с ном. кр.3-ем.

 Типы
фильтров:1 НЧФ - низкочастотный ф.
предназначен для пропускания к
приемнику
Типы
фильтров:1 НЧФ - низкочастотный ф.
предназначен для пропускания к
приемнику
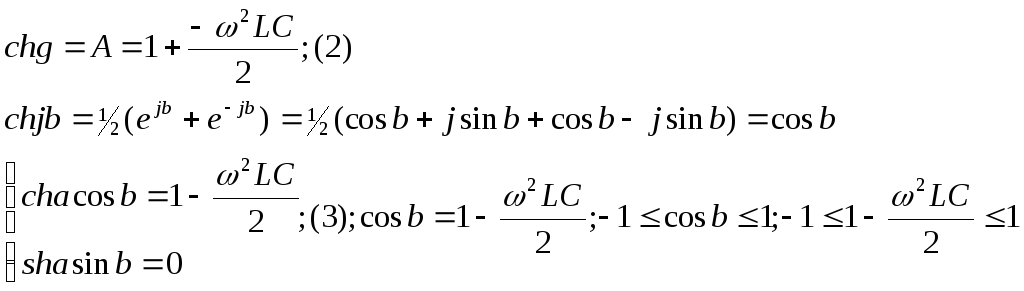



 2
2

