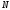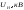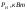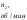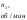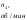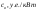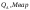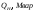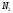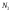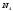Алматинский университет энергетики и связи.
Расчетно-графическая работа
по дисциплине:
«МАТЕМАТИЧЕСКИЕ ЗАДАЧИ И
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ В ЭЛЕКТРОЭНЕРГЕТИКЕ»
Выполнил: студент группы БЭк-10-03
Алибаева А. А.
Номер зачетной книжки: 104005
Вариант: А05
Проверила: Асанова К.М.
Дата сдачи: « » ___________ 2012 г.
Алматы 2012
Содержание
Введение…………………………………………………………………………...3
Основная часть
Задание №1………………………………………………………………………...4
Задание №2………………………………………………………………………...6
Задание №3………………………………………………………………………...9
Заключение……………………………………………………………………….16
Список использованной литературы………………………….………………..17
Введение
Данная расчетно-графическая работа предназначена для закрепления теоретического материала, пройденного на лекционных и практических занятиях.
Расчетно-графическая работа включает в себя 3 задания.
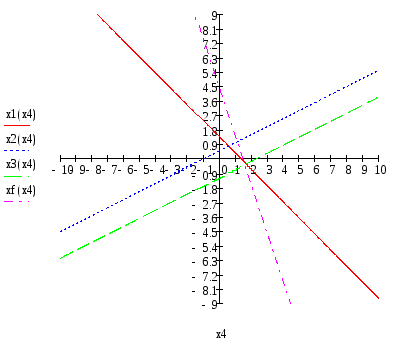
В первом задании нужно решить систему линейных уравнений графическим методом. Также нужно построить область допустимых решений и определить точку экстремума функции.
Во втором задании методом неопределенных множителей Лагранжа нужно определить оптимальную реактивную мощность синхронных двигателей.
А в третьем задании нужно определить вероятность нагрузки трансформаторов питающей подстанции; математическое ожидание, дисперсию, среднеквадратичное отклонение случайной величины нагрузки трансформатора; показатели надежности системы электроснабжения относительно шин 0,4 кВ; величину недоотпущенной электроэнергии за год относительно шин 0,4 кВ.
№ 1 Задание
Решить систему линейных уравнений графическим методом. Построить область допустимых решений и определить точку экстремума функции, согласно заданию.
Исходные данные для задачи принимаются по таблице 1.1, согласно правилам выбора вариантов.
Дано:
С1=2;
С2=1;
С3=-1;
С4=-1;
f(x)=min;
a11=2; a21=2; a31=-1; b1=1;
a12=-1; a22=1; a32=4; b2=2;
a13=1; a23=1; a33=-2; b3=3;
a14=2; a24=1; a34=-2; b4=-
Знаки ограничений:
1) ≤
2) ≤
3) ≤
Решение:
Данная задача решается с помощью программы Mathcad. Для этого вводим данные, соответствующие уравнению функции, и данные, соответствующие уравнениям ограничений. Задаем требования по выполнению принципа неотрицательности полученных решений. Строим на графике область допустимых решений и вектор-потенциал, по его направлению определяем точку экстремума функции и ее координаты. Определяем значение функции и переменных в точке экстремума.
![]()
![]()
![]()
![]()
![]()
![]()
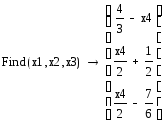
![]()
![]()
![]()
![]()
№ 2 Задание
К шинам РУ 6-10 промышленного предприятия присоединены N синхронных электродвигателей, требуется с помощью метода неопределенных множителей Лагранжа определить оптимальную реактивную мощность от каждого из синхронных двигателей, пренебрегая сопротивлениями кабелей. Реактивная нагрузка, подлежащая компенсации на стороне 6-10 кВ, определяется вариантом задачи. Данные к задаче для каждого из вариантов принимаются по таблицам 2.1, 2.2 и 2.3. Технические характеристики двигателей приведены в таблице 2.4.
Дано:
|
|
|
|
|
|
|
|
|
|
|
4 |
6 |
1000 |
1000 |
600 |
500 |
250 |
55 |
0,8 |
|
|
|
|
|
|
|
|
1000 |
0,511 |
5,09 |
3,99 |
|
|
600 |
0,511 |
7,66 |
5,38 |
|
|
500 |
0,511 |
6,61 |
5,88 |
|
|
250 |
0,520 |
10,0 |
7,19 |
Решение:
1) Определим максимальную реактивную мощность от каждого синхронного двигателя:
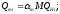 (2.1)
(2.1)
где αm – коэффициент учитывающий максимальную реактивную мощность. (αm=1.39 = const.)
M – количество двигателей, имеющих одинаковую мощность и скорость вращения (М=1).
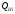 -
номинальная реактивная мощность.
-
номинальная реактивная мощность.
Подставляем числовые данные:
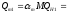 1.39
1.39 1
1 0,511=0.71029
МВар;
0,511=0.71029
МВар;
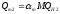 = 1.39
= 1.39 1
1 0,511=0.71029
МВар;
0,511=0.71029
МВар;
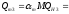 1.39
1.39 1
1 0,511=0,71029
МВар;
0,511=0,71029
МВар;
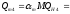 1.39
1.39 1
1 0,520=0,7228
МВар;
0,520=0,7228
МВар;
2) Определим составляющие затрат на выработку реактивной мощности синхронными двигателями:
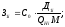 (2.2)
(2.2)
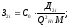 (2.3)
(2.3)
где
С0 – удельная стоимость, у.е./кВт;
Д1 и Д2 – величины двигателей, кВт;
Q Hi – номинальная реактивная мощность, МВАр;
М – количество синхронных двигателей в группе имеющих одинаковую мощность и скорость вращения.
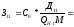
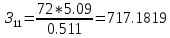
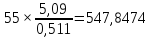 у.е./МВАр;
у.е./МВАр;
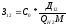 =
=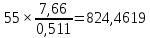 у.е./МВАр;
у.е./МВАр;
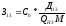 =
=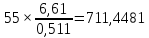 у.е./МВАр;
у.е./МВАр;
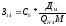 =
=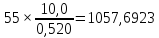 у.е./МВАр;
у.е./МВАр;
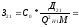
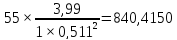
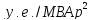 ;
;
З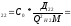
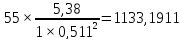
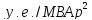 ;
;
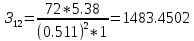
З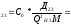
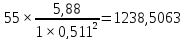
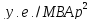 ;
;
З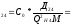
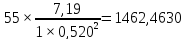
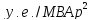 ;
;
3) Составим функцию Лагранжа:
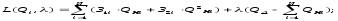
(2.4)
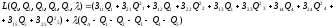
Определим неопределенный множитель Лагранжа:
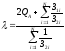
(2.5)


5) Определим оптимальную реактивную мощность от каждого синхронного двигателя:
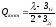
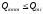
(2.6)
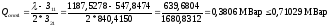
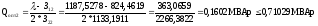
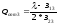 =
=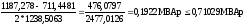
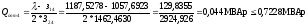
6) Правильность расчетов определяем по балансу реактивной мощности:
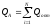 (2.7)
(2.7)
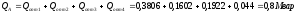
По вычисленным формулам я убедилась в правильности выполненных расчетов:
0,8=0,8