7 Энергия гармонических колебаний
Из механики известно,
что квазиупругая сила
является
консервативной, поэтому полная энергия
гармонических колебаний должна оставаться
постоянной. При колебаниях происходит
превращение Ер
в Ек
и обратно.
При х = А
.
(7)
При х = 0
.
(8)
Зависимость их от времени определяется выражениями:
.
.
Полная энергия:
.
(9)
Т.О. полная энергия действительно остается постоянной.
Используя тригонометрические соотношения:
и
,
получим, что Ек и Ер изменяются с частотой 2ω.
8
Пружинный маятник-
это груз массой m,
подвешенный на абсолютно упругой пружине
и совершающий гармонические колебания
под действием упругой силы
формула периода справедлива , когда масса пружины мала по сравнению с массой тела
Потенциальная
энергия пружинного маятника:
9 Векторная диаграмма.
Возьмем ось Х. Из точки О отложим вектор длины А под углом α к оси Х и будем его вращать с угловой скоростью ω0. Тогда проекция конца вектора будет перемещаться вдоль х от –А до +А, а координата проекции будет изменяться со временем по закону:
,
т.е. будет совершать гармоническое колебание с амплитудой А, равной длине вектора, круговой частотой, равной угловой скорости вращения вектора, и начальной фазой, равной углу α между вектором и Х в начальный момент времени. Другими словами гармонические колебания можно изображать с помощью векторов.
Сложение колебаний одинакового направления.
Запишем 2 колебания вдоль оси Х:
и
Из рис.2 видно, что х = х1 + х2
и
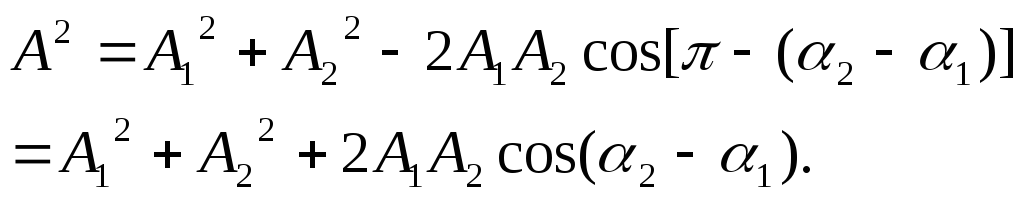(10)
.
(11)
Биения
При сложении двух гармонических колебаний одинакового направления, мало отличающихся по частоте возникают биения. Их можно рассматривать как гармоническое колебание с пульсирующей амплитудой. По условию
и
Результирующее колебание:
(12),
где
амплитуда =
,
т.к. она не может быть отрицательной.
Частоту
пульсаций амплитуды называют частотой
биений и она равна
.
10 Сложение взаимно-перпендикулярных колебаний
Примем начальную фазу 1-го колебания равной 0. Тогда
и
,
(1)
где
- разность фаз обоих колебаний.
Для получения траектории исключим параметр t.
.
Тогда
.
(2)
и
.
После преобразований получим:
.
(3)
Уравнение эллипса. Исследуем форму траектории в зависимости от разности фаз и амплитуд.
1)
.
Тогда (3):
или
.
(4)
Точка
колеблется вдоль прямой
, (5)
полученной
из (1) с учетом того, что
.
Вывод ?
2)
.
Тогда (3) примет вид:
,
откуда
.
(4/)
3)
.
Тогда получим эллипс:
.
(5)
Если
,
то эллипс вырождается в окружность.
дает
разные направления (анализ следует из
(1), + соответствует движению по часовой
стрелке.
Фигуры Лиссажу
1)
При
и
получим уравнения колебаний:
,
.
Пока вдоль ОХ точка смещается из одного крайнего положения в другое, вдоль оси ОУ, выйдя из нулевого положения, она успевает достигнуть одного крайнего, затем другого и вернуться в нулевое (исходное) положение.
2) При
и
получаем незамкнутую кривую, по которой
движется точка туда и обратно.
Чем ближе к единице дробь, тем сложнее фигура Лиссажу.
3)
Рассмотрим
и
.
Фигуры
Лиссажу -
замкнутые траектории точки М, одновременно
совершающей гармонические колебания
в двух взаимно-перпендекулярных
направлениях. Форма фигур зависит от
соотношения амплитуд, частот и начальных
фаз складываемых колебаний:
, где p и q - целые числа. Значения координат
колеблющейся точки М одновременно
повторяются через одинаковые промежутки
времени Т0 , равные общему наименьшему
кратному
- периодов колебаний вдоль осей ОХ и ОУ.
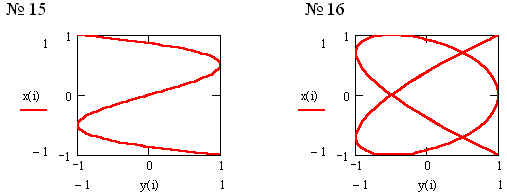
Отношение частот
равно отношению числа касаний
соответствующей им фигуры Лиссажу со
стороной прямоугольника, параллельной
оси ОУ, и со стороной, параллельной оси
ОХ. В таблице приведены параметры
соответствующих, представленных ниже
на рисунках системы MathCAD, 20 фигур Лиссажу.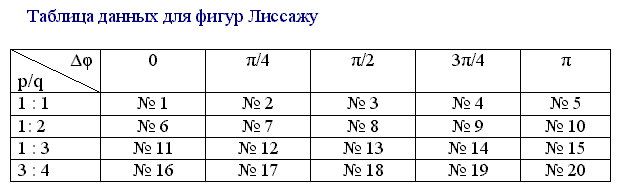
11
Колебательным называется
контур,
состоящий из катушки индуктивности L
и конденсатора С, в котором могут
возникнуть электрическое колебания
(рис.1). Рассмотрим этот процесс: Пусть
верхняя обкладка С заряжена положительно.
Вся энергия заключена в С. При замыкании
ключа, С разряжается, через L
течет ток. Электрическая энергия С
переходит в магнитную энергию катушки
(через
),
далее ток убывает (не сразу с учетом
явления самоиндукции), а положительный
заряд переходит на нижнюю обкладку С
(через следующие
),
т.е. через полпериода энергия вновь
полностью переходит в электрическую.
С этого момента С вновь начнет разряжаться,
ток потечет в обратном направлении и
т.д. – процесс будет повторяться.
При
(активное сопротивление контура)
происходят строго периодические
колебания. При
часть
энергии переходит в тепло, будут
затухающие колебания.
Получим
общее уравнение колебательного контура,
содержащего последовательные С, L,
R
и внешнюю переменную ЭДС
.
(Рис.2).
Выберем положительное направление обхода и соответствующий ему переход заряда. Тогда
.
(1)
Для участка 1RL2 по закону Ома
.
(2)
Здесь
и
.
Тогда (2) перепишем в виде
или
.
(3)
Чаще пишут уравнение колебательного контура в виде
(4)
где
(или
)
и
.
(5)
Если
,
колебания называются ?
Если
,
колебания называются ?
Если
,
колебания называются ?