
- •1. Энергия магнитного поля.
- •4 Экстратоки размыкания и замыкания в электрических цепях.
- •5 Ток смещения
- •7 Энергия гармонических колебаний
- •9 Векторная диаграмма.
- •10 Сложение взаимно-перпендикулярных колебаний
- •12 Свободные затухающие колебания
- •13 Установившиеся колебания. Амплитуда и фаза вынужденных колебаний.
- •114 Переменный эл ток. З-н Ома для переменного тока
- •15 Работа и мощность переменного тока
- •18 Энергия упругой волны
- •23 Интерференция световых волн
- •25 Дифракция Френеля от круглого отверстия.
- •27 Поглощение и рассеяние света. Поляризация света. З-ны Малюса и Брюстера
- •30, 31 Тепловое излучение. З-ны теплового излучения. Проблема теплового излучения абсолютно черного тела.
- •31 Квантовая гипотеза и формула Планка.
- •32 Фотоэффект и его з-ны. Ур-е Эйнштеина
- •33 Фотоны. Энергия и импульс световых квантов
- •36 Теория Бора для водородоподобных атомов. Опыты Франка и Герца.
- •37 Экспериментальные подтверждения гипотезы и формулы де Бройля
- •40 Частица в потенциальной яме
- •41 Прохождение частицы через потенциальный барьер
- •42 Линейный гармонический осциллятор в квантовой механике. Нулевая энергия.
- •43 Атом водорода
- •45 Спонтанное и вынужденное излучения. Лазеры.
- •50 Энергетические зоны в кристаллах. Металлы, диэлектрики и полупроводники в зонной теории твердых тел.
- •51 Элементы квантовой теории проводимости металла. Явл-ие сверхпроводимости
- •52 Полупроводники
- •53 Контакт эл и дыр полупров. Полупров диод.
- •54 Вырожденный эл газ в металле. Уровень Ферми.
- •55 Атомное ядро и его характеристики. Состав и строение атомного ядра. Изотопы.
- •56 Дефект массы и энергия связи ядра.
- •58 Ядерные силы и их основные свойства.
- •60 Радиоактивный распад ядер. Закономерности и происхождение альфа-, бета-, гамма-излучений.
- •61 Яд реакции и законы сохр.
33 Фотоны. Энергия и импульс световых квантов
Фотоны- элементарная частица, к-ая всегда движется со скоростью света и имеет массу покоя, равную нулю.
Энергия
фотона:
![]() Масса
фотона:
Масса
фотона:![]() Импульс
фотона:
Импульс
фотона: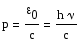
Фотон как и любая другая частица, х-ся энергией, массой и импульсом
34
В 1923 г. А.
Комптон,
исследуя рассеяние рентгеновских лучей
различными веществами, обнаружил, что
в рассеянных лучах наряду с излучением
первоначальной длины волны
![]() содержатся также лучи большей длины
волны
содержатся также лучи большей длины
волны![]() .
Оказалось, что
.
Оказалось, что
![]() (4)
(4)
![]() -
угол рассеяния, т.е. разность
-
угол рассеяния, т.е. разность
![]() от длины волны
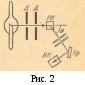
от длины волны![]() и от природы вещества не зависит. Схема
опыта показана на рис. 2.
и от природы вещества не зависит. Схема
опыта показана на рис. 2.
Эффект
Комптона объясняется, представив
рассеяние как процесс упругого
столкновения рентгеновских фотонов с
почти свободными электронами. Если на
первоначально покоящийся свободный
электрон падает фотон с энергией
![]() и импульсом
и импульсом![]() (рис. 3), то используя законы сохранения
энергии и импульса, можно получить
формулу (4).
(рис. 3), то используя законы сохранения
энергии и импульса, можно получить
формулу (4).
г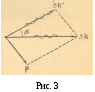 де
де
![]() (6)
(6)
носит название комптоновской длины волны. Определяемая выражением (6) дает для комптоновской длины волны электрона значение
![]()
36 Теория Бора для водородоподобных атомов. Опыты Франка и Герца.
1
постулат Бора: (постулат стационарных
состояний) в атоме существуют стационарные
состояния, в к-ых он не излучает энергии.
Стационарным состояниям атома
соответствуют стационарные орбиты, по
к-ым движутся электроны. Движение
электронов по стационарным орбитам не
сопровождается излучением электромагнитных
волн. В стационарном состоянии атома
электрон, двигаясь по круговой орбите,
должен иметь дискретные квантованные
значения момента импульса, удовлетворяющие
условию
![]() (n = 1, 2, 3…)
(n = 1, 2, 3…)
2
постулат Бора: (правило частот) при
переходе электрона с одной стационарной
орбиты на другую излучается(поглощается)
один фотон с энергией
![]() равной разности энергий соответствующих
стационарных состояний. Если
равной разности энергий соответствующих
стационарных состояний. Если![]() то происходит излучение фотона. Если
то происходит излучение фотона. Если![]() - поглощение.
- поглощение.
Опыты
Франка и Герца показали, что электроны
при столкновении с атомами ртути передают
им только определенные порции энергии
(подтверждение идеи Бора). Атомы ртути,
получившие при соударении с электронами
энергию
![]() переходят в возбужденное состояние и
должны возвратиться в основное, излучая
световой квант.
переходят в возбужденное состояние и
должны возвратиться в основное, излучая
световой квант.
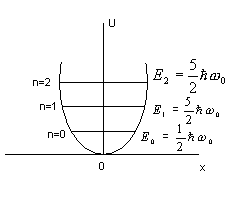
37 Экспериментальные подтверждения гипотезы и формулы де Бройля
Опыты Девиссона и Джермерра. При заданном угле падения электроны отражаются от пов-ти кристалла под различными углами, причем в одних направлениях наблюдаются максимумы числа отраженных электронов, в других – минимумы, т.е. наблюдалась диф картина. Это явление наблюдается когда длина электронной волны де Бройля имеет порядок межатомного расстояния в кристалле. Длина волны , связанная с электронами, порядка длины волны рентгеновских лучей. Физ смысл волн де Бройля:квадрат амплитуды волны де Бройля в данной точке пр-ва явл-ся мерой вероятности обнаружить частицы в этой точке пр-ва.
38 Соотношение неопределенностей Гейзенберга
к вантовая
механика раскрывает 2 основных св-ва
вещ-ва: квантованность внутриатомных
процессов и волновую природу частиц.
Скорость света в вакууме явл-ся критерием,
определяющим границу применимости
классических з-нов, т.к. она явл-ся макс
скоростью передачи сигналов.
вантовая
механика раскрывает 2 основных св-ва
вещ-ва: квантованность внутриатомных
процессов и волновую природу частиц.
Скорость света в вакууме явл-ся критерием,
определяющим границу применимости
классических з-нов, т.к. она явл-ся макс
скоростью передачи сигналов.
Т.к.
движущая частица обладает корпускулярно-
волновым дуализмом, то одновременное
точное определение координаты х и
импульса р невозможно. Чем точнее
определена координата (![]() )
тем менее точно определен импульс (
)
тем менее точно определен импульс (![]() )
)
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку величины меньше постоянной Планка, называется принципом неопределенности Гейзенберга.
![]()
![]()
![]()
39 Уравнение Шредингера(1926 г.)
![]() . (11)
. (11)
![]() комплексная
функция координат и времени, характеризует
состояние микрочастицы. Это основное
уравнение нерелятивистской квантовой
механики. Для стационарных состояний
оно имеет вид:
комплексная
функция координат и времени, характеризует
состояние микрочастицы. Это основное
уравнение нерелятивистской квантовой
механики. Для стационарных состояний
оно имеет вид:
![]() . (12)
. (12)
М.
Борн (1926 г) впервые дал интерпретацию
пси – функции: квадрат модуля
![]() функции
определяет вероятность dP того, что
частица будет обнаружена в пределах
объема dV
функции
определяет вероятность dP того, что
частица будет обнаружена в пределах
объема dV
![]() (13)
(13)
А - коэффициент пропорциональности, для пси-функции выполняется следующее условие нормировки:
![]() (14)
(14)
Из
смысла
![]() функции(волновая)
вытекает, что квантовая механика имеет
статистический характер. Уравнение
Шредингера позволяет найти пси – функцию
данного состояния и, следовательно,
определить вероятность нахождения
частицы в различных точках пространства.
Из уравнения (14) и условий, налагаемых
на пси – функцию, непосредственно
вытекают правила квантования энергии.
функции(волновая)
вытекает, что квантовая механика имеет
статистический характер. Уравнение
Шредингера позволяет найти пси – функцию
данного состояния и, следовательно,
определить вероятность нахождения
частицы в различных точках пространства.
Из уравнения (14) и условий, налагаемых
на пси – функцию, непосредственно
вытекают правила квантования энергии.
Пси – функция должна быть однозначной, непрерывной и конечной, кроме того она должна иметь непрерывную и конечную производную – стандартные условия.
