

№ 4 (18.70)
Условие:
Найти вероятность событий C, D при бросании двух игральных костей.
C = {Сумма очков четна}, D = {Сумма очков больше двух}.
Решение:
В данной задаче лучше всего воспользоваться классической схемой случаев. Пространство элементарных исходов это множество упорядоченных пар чисел, выпавших на кубиках (числа от 1 до 6).
-
Найдем количество всевозможных исходов. На 2 костях возможно выпадение 62 упорядоченных комбинаций. Следовательно, всего возможных исходов - N(Ω) = 36.
-
Событие С произойдет в том случае, если на обоих зариках выпадет оба четных числа, либо оба нечетных. Порядок выпадения не важен. Следовательно, количество возможных исходов в случае выпадения нечетного числа (1,3,5) равно трем, т.к. на втором кубике также должно выпасть нечетное число. Аналогично для четных чисел (2,4,6). А поскольку порядок выпадения не важен, тогда общее число исходов удваивается.
N(C) = (3*3) *2 = 18
-
Событие D произойдет в том случае, если на зариках выпадут любые числа, кроме двух единичек. Количество возможных исходов подсчитаем от обратного, найдя количество исходов противоположного события, а так как возможен всего один исход, тогда N(D) = N(Ω) - 1 = 36 – 1 = 35
-
Тогда вероятность событий С и D:
P(C)
=
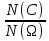 =
=

P(D)
=
 =
=

Ответ: P(C) = 0,5; P(D) = 0,97

