МДЗ №1

Оформил: студент НИУ МИЭТ

группы МП-23

Шлыков Максим Сергеевич

Оглавление

МДЗ №1 1

Оглавление 2

Задача 18.25 3

Решение задачи: 3

Задача 18.40 5

Решение задачи: 5

Задача 18.55 7

Доказательство: 7

Задача 18.70 9

Задача 18.85 11

Задача 18.100 13

Задача 18.115 14

Задача 18.130 15

Задача 18.145 16

Задача 18.160 17

Задача 18.25

Формулировка задачи:

Доказать тождество .

Поскольку событие отождествляется с множеством, то над событиями (в том числе А, В и С) можно совершать операции, выполнимые на множествами.

Список допустимых операций выглядит так:

1. A = B - Событие А тождественно событию B.

2. A 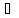B - Событие А влечет за собой событие B.

3. A + B - Сумма событий.

4. AB - Произведение событий.

5. A - B - Разность событий.

6. - Противоположное событие

Операции над событиями также обладают рядом свойств, которые мы будем использовать для решения задачи.

1. Коммутативность сложения и умножения:

   1. A + B = B + A ;

   2. AB = BA .

2. Ассоциативность:

   1. (A+B)+C = A+(B+C) ;

   2. (AB)C = A(BC) .

3. Дистрибутивность:

   1. (A+B)C = AC + BC ;

   2. AB+C = (A+C)(B+C) .

4. Правило де Моргана:

   1. ;

   2. .

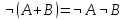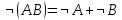5. Законы поглощения:

   1. AA = A ;

   2. A + A = A ;

   3. A + Ω = Ω ;

   4. AΩ = A ;

   5. A + Ø = A ;

   6. AØ = Ø .

Решение задачи:

Путем преобразований над А , В и С из левой части тождества получим правую.

- далее будем выписывать только левую часть и этапы её преобразований до тех пор, пока не получим выражение «» .

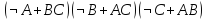- перемножим первые два слагаемых.

Получим: . Обратим внимание, что выделенные события являются невозможными, так как содержат произведение несовместных исходов. Их можно исключить. Также слагаемое можно упростить в соответствии с законом поглощения: (CC = C) .

Имеем два слагаемых: 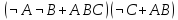- перемножим их.

Получим : . События и 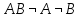удаляем как невозможные, а упростим в соответствии с законом поглощения : .

В итоге получается следующее выражение: - оно же и является правой частью тождества. Тождество доказано.

Задача 18.40

Формулировка задачи:

Электрическая цепь составлена по схеме, приведенной на рисунке.

Событие A_k = { элемент с номером k вышел из строя } , где k = 1, 2, 3, 4, 5.

Cобытие B = { разрыв цепи } .

Выразить событие B в алгебре событий A_1, A_2, A_3, A_4, A_5.

Решение задачи:

Проанализируем понятие разрыва цепи. Оно подразумевает, что между точками O и N - на схеме, не будет проходить ток. Это означает, что и в любой из трех веток заданной цепи ток также проходить не будет, иначе условие бы не выполнялось. Далее рассуждаем последовательно.

В верхней ветке цепи, содержащей элементы 1 и 2, затруднение прохождения тока может быть вызвано выходом из строя одного из этих элементов, либо обоих одновременно. Аналогично с нижней ветвью цепи, содержащей элементы 4 и 5. В центральной же ветке с элементом 3, выход из строя обязателен при разрыве цепи, иначе ток пройдет по ней беспрепятственно.

В итоге мы можем сказать, что для B - события необходимо выполнение целой совокупности событий:

B =

или

B =

Тогда решением будет выражение :

B = (A₁ + A₂)(A₄+A₅)A_{3 .}

Задача 18.55

Формулировка задачи:

Доказать справедливость формулы сложения вероятностей:

P(A + B) = P(A) + P(B) - P(AB) .

Начнем с того, что вероятностью P(A) называется числовая функция определенная для всех AF (где F - поле событий для данного эксперимента) и удовлетворяющая трем условиям (аксиомам вероятностей):

1. P(A) 0 (аксиома неотрицательности)

2. P(Ω) = 1 (аксиома нормированности)

3. P(A+B) = P(A) + P(B) при A,B 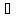F: AB = Ø (аксиома сложения)

Так как событие есть множество, то вероятность является также функцией множества. Указанные аксиомы выделяют специальный класс числовых функций, являющихся вероятностями.

Доказательство:

Для начала обратим внимание что: . В этом не трудно убедиться, изобразив тождество в виде диаграмм Эйлера.

Поскольку ) = Ø, то из аксиомы сложения (аксиомы 3) следует, что

. (1)

Далее, (в чем также не трудно убедиться из следующей диаграммы).

Также из 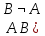) = Ø и аксиомы 3 следует, что P(B) = P(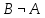)+ P(AB). (2)

Выражая из (2) и подставляя в (1) получаем:

P(A + B) = P(A) + P(B) - P(AB).

Справедливость формулы сложения вероятностей доказана.

Задача 18.70

Формулировка задачи:

Найти вероятность событий C, D при бросании двух игральных костей. C = {Сумма очков четна}, D = {Сумма очков больше двух}.

Решение:

Для нахождения вероятности событий воспользуемся схемой случаев. Определим пространство элементарных исходов. Это множество упорядоченных пар чисел. Каждый элементарный исход характеризуется последовательностью двух чисел от 1 до 6. Предложенная схема случаев предполагает равновозможность и несовместность элементарных исходов, а также описывает все возможные события для данного опыта.

Найдем количество всевозможных исходов. На каждой кости может выпасть от 1 до 6 очков. Тогда на 2 костях возможно выпадение 6² упорядоченных комбинаций.

Итого: N(Ω) = 36 - всего возможных исходов.

Проанализируем заданные события: C = {Сумма очков четна}, D = {Сумма очков больше двух}.

События не учитывают порядок выпадения чисел на костях, а потому (4;2) и (2;4) оба входят в событие C. Событие D происходит всегда, когда на одной из костей выпадает больше 1. Иными словами противоположный событию D исход наступает только при выпадении 1 на обеих костях.

Найдем количество возможных исходов для событий C и D.

Для события С в случае выпадения нечетного числа (1,3 или 5) очков на первой кости, возможно только 3 подходящих исхода, когда выпадет нечетное число на второй кости (три нечетных числа 1, 3, 5).

Аналогично при выпадении четного числа (2, 4 или 6) очков на первой кости, но в этом случае возможно 3 подходящих исхода, когда выпадет четное число на второй кости (три четных числа 2, 4, 6).

Поскольку порядок не важен общее число исходов можно удвоить, получаем:

m(C) = (3*3) *2 = 18.

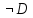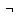Для D найдем количество исходов противоположного события, т.е. D. Возможен всего один исход , т.е. m() = 1. А поскольку D + D = Ω, то

m(D) = 36 - 1 = 35.

Найдем вероятность событий С и D:

P(C) = =

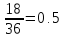
P(D) = =

Задача 18.85

Формулировка задачи:

Из урны содержащей m₁ шаров с номером 1, m₂ шаров с номером 2, … , m_s шаров с номером s, наудачу без возвращения извлекается n шаров. Найти вероятности событий: A = {появится n₁ шаров с номером 1, n₂ шаров с номером 2, … , n_s шаров с номером s}; B = {не появятся шары с номерами 1 или 2} .

Решение:

Поскольку опыт состоит в выборе n элементов без повторения и без упорядочивания, то различными исходами следует считать n-элементные подмножества множества m₁ + m₂ + … + m_s для данной задачи , имеющие различный состав. Получаемые при этом комбинации элементов являются сочетаниями из m₁ + m₂ + … + m_s по n. Тогда общее число возможных исходов равняется:

N(Ω) =

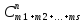
Проанализируем предложенные события.

Событию A благоприятствует исход, когда из m ₁ шаров с номером 1 будут выбраны любые n ₁, из m ₂ шаров с номером 2 будут выбраны любые n ₂, … и так далее (при этом n₁+ n₂ +…+ n_s = n). Тогда из m ₁ можно выбрать n ₁ шаров числом способов, из m ₂ можно выбрать n ₂ шаров числом способов, и т. д. Исходы, связанные с шарами под различными номерами никак не связаны между собой, а потому мы можем их перемножить. Получаем:

m(A) =

Событию B благоприятствует исход, при котором n шариков будет выбрано из m₃ + m₄ + … + m_s шаров (m₁ и m₂ в эту сумму не входят). Количество таких исходов будет равно:

m(B) =

Вероятность событий A и B:

P(A) = =

P(B) = =

Задача 18.100

Формулировка задачи:

Бросается 10 одинаковых игральных костей. Вычислить вероятности следующих событий: A = { ни на одной кости не выпадет 6 очков}, B = { хотя бы на одной кости выпадет 6 очков}, C = { ровно на 3 костях выпадет 6 очков}.

Решение:

Заметим, что событие B является противоположным событию A, а потому P(B) = 1 - P(A). Найдем сначала вероятность события A.

Вероятность выпадения очков на каждой кости не зависит от выпадения очков на всех других костях. Поэтому вероятность события А равна произведению вероятностей выпадения от 1 до 5 очков на каждой кости. Получаем:

P(A) = (5/6)*(5/6)*…*(5/6) = (5/6)¹⁰ = 0,1615 Тогда:

P(B) = 1 - P(A) = 1- 0,1615 = 0,8385.

Задача 18.115

Формулировка задачи:

52 карты раздаются четырем игрокам (каждому по 13 карт). Найти вероятности следующих событий: C = { все тузы попадут к одному из игроков }, D = { двое определенных игроков не получат ни одного туза }.

Задача 18.130

Формулировка задачи:

Из множества чисел E = { 1, 2, … , n } выбирается три числа. Какова вероятность того, что второе число заключено между первым и третьим, если выбор осуществляется: a) без возвращения; б) с возвращением ?

Задача 18.145

Формулировка задачи:

Какова вероятность, не целясь, попасть бесконечно малой пулей в прутья квадратной решетки, если толщина прутьев равна а, а расстояние между их осями равно l (l > a).

Задача 18.160

Формулировка задачи:

Пусть А, B и С - наблюдаемые события, причем P(C) > 0, P(AC) > 0. Доказать справедливость следующих формул для условной вероятности:

P(AB|C) = P(A|C) P(B|AC) (формула умножения),

P(A+B|C) = P(A|C) + P(B|C) - P(AB|C) (формула сложения ).