Логика / lect8_m1_vm1_vt_lta_230100.62_niy06

Лекция 7. Лемма Цорна. Теорема Цермело.

Определение. Пусть – частично упорядоченное множество и Г – его подмножество, являющееся цепью. Мажорантой (или верхней границей) цепи Г называется любой элемент такой, что для всех

Обозначим через множество всех мажорант цепи Г. Введём ещё одно обозначение. Пусть Г – цепь и Положим

Наша дальнейшая цель – сформулировать два новых утверждения – лемму Цорна и теорему Цермело – и доказать их эквивалентность аксиоме выбора.

1. Аксиома выбора (формулировка была раньше).

2. Лемма Цорна. Пусть – частично упорядоченное множество, в котором каждая цепь имеет мажоранту. Тогда имеет хотя бы один максимальный элемент.

3. Теорема Цермело. На всяком множестве можно ввести отношение порядка, превращающее его во вполне упорядоченное множество.

Ввиду эквивалентности каждое из этих утверждений с одинаковым успехом может быть принято в качестве аксиомы, тогда две другие будут являться теоремами. Обычно за аксиому принимают первое утверждение – аксиому выбора ввиду её простоты и достаточной очевидности.

Замечание. Аксиома выбора так же, как лемма Цорна и теорема Цермело, носят неконструктивный характер. Аксиома выбора утверждает, что существует функция выбора, но не говорит о том, как её построить. Теорема Цермело утверждает, что всякое множество можно сделать вполне упорядоченным, но как это сделать, из теоремы извлечь невозможно. Никому ещё не удалось вполне упорядочить несчётное множество (скажем, множество действительных чисел). Некоторые математики – конструктивисты – не признают “голых теорем существования”, т.е. теорем, не дающих способа построения объекта, а лишь доказывающих существование этого объекта. Вместе с тем большинство математиков признаёт аксиому выбора и вытекающие из неё утверждения и считает её частью математического знания, источником получения других результатов.

Далее мы увидим, что с помощью аксиомы выбора, леммы Цорна и теоремы Цермело можно доказать некоторые утверждения, доказательство которых другими методами неизвестно. В частности, сейчас мы докажем, что любые два множества сравнимы по мощности.

Теорема 2. Для любых двух множеств и справедливо хотя бы одно из следующих соотношений:

Теорема 3. Пусть – бесконечное множество мощности Тогда:

(а) можно разбить на два непересекающихся подмножества, мощность каждого из которых равна

(б) можно разбить на непересекающихся двухэлементных подмножеств.

Следствие 1. Если – бесконечная мощность, то (объединение двух непересекающихся множеств мощности имеет мощность (объединение непересекающихся двухэлементных множеств имеет мощность

Следствие 2. Если и – бесконечные мощности, то

Доказательство. Пусть, например, Ввиду следствия 1 получаем: откуда

Следствие 3. Пусть и – бесконечные множества (возможно, пересекающиеся). Тогда

Доказательство. Пусть, например, Тогда откуда следует, что

Следствие 4. Если – бесконечное множество, – множество такое, что то

1. Доказать, что всякое линейное пространство имеет базис.

2. Доказать, что всякое ненулевое кольцо с единицей имеет максимальный идеал, не совпадающий со всем кольцом.

3. Доказать, что в любом частично упорядоченном множестве частичный порядок может быть продолжен до линейного.

Задачи для самостоятельного решения

1. (а) Доказать, что если – группа и 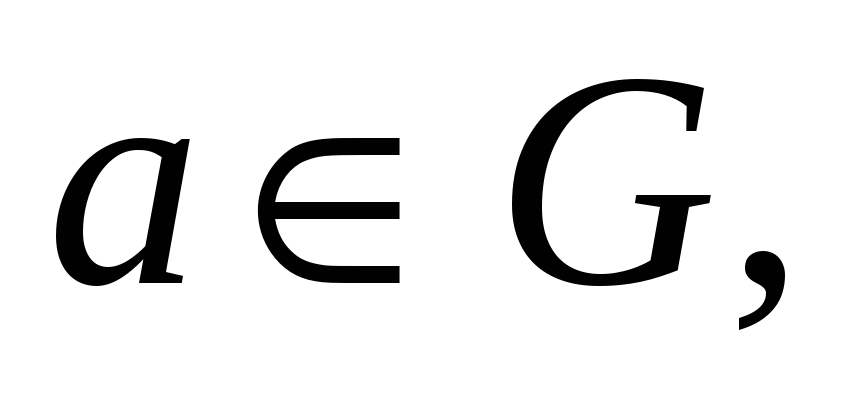то существует в группе максимальная (по включению) подгруппа, не содержащая элемента

(б) Верно ли, что в любой группе есть максимальная подгруппа

Ответ: (б) Нет. Например, группа – объединение цепочки групп – такова, что все её подгруппы, отличные от неё самой, конечны и ни одна из них не максимальна.

2. Назовём антицепью множество элементов частично упорядоченного множества, которые попарно не сравнимы друг с другом. Доказать утверждения:

(а) всякое частично упорядоченное множество содержит хотя бы одну максимальную (по включению) цепь (теорема Куратовского – Хаусдорфа);

(б) всякое частично упорядоченное множество содержит максимальную антицепь.

3. Доказать, что всякий связный граф (не обязательно конечный) содержит максимальное дерево.

4. Подмножество 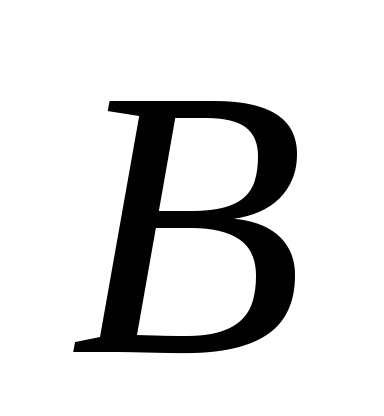линейно упорядоченного множества назовём конфинальным, если Доказать, что всякое линейно упорядоченное множество содержит конфинальное вполне упорядоченное подмножество.

5. Будем говорить, что частично упорядоченное множество удовлетворяет условию минимальности, если в нём нет бесконечных убывающих цепей элементов. Доказать, что множество удовлетворяет условию минимальности в том и только том случае, если все его цепи вполне упорядочены.

6. Пусть – частично упорядоченное множество, в котором каждая цепь имеет мажоранту. Доказать, что для любого в множестве есть максимальный элемент такой, что

7. Пусть – множество и 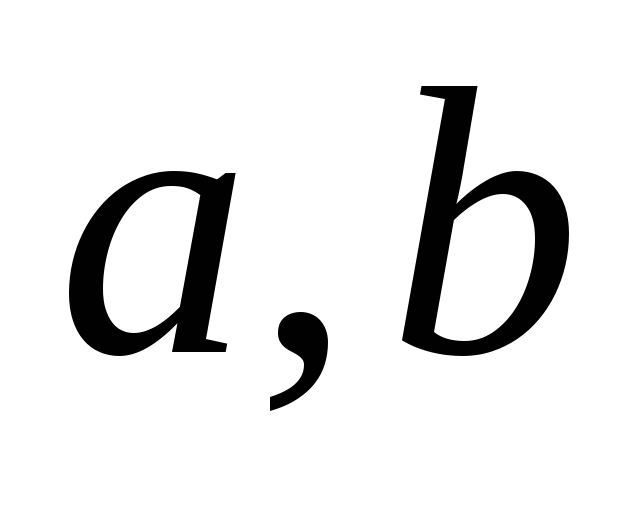– какие-либо его различные элементы. Доказать, что существует максимальное (по включению) отношение эквивалентности на такое, что Сколько классов эквивалентности имеет отношение

Ответ: два.

3